prior과 posterior

그냥 데이터마이닝을 공부하다 강화학습에서 나오는 prior과 posterior에 대해서 나오길래
기록할겸 작성한다.

prior과 posterior

강화학습을 공부할 때 prior과 posterior이 나오는데
이는 어떤 것을 의미할까?

원칙적으로 prior은 사전분포, posterior은 사후분포를 의미한다.

베이즈 정리를 보면
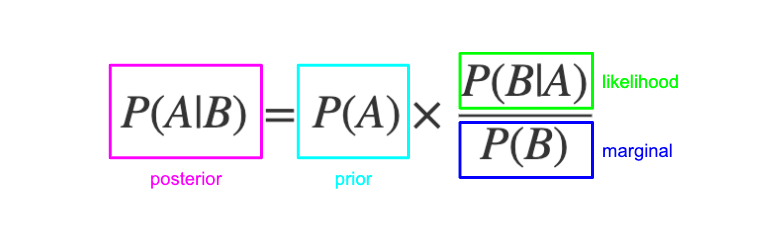출처
위와 같이 prior과 posterior이 나오게 된다.

이게 정확하게 무엇을 의미할까?
예시를 한번 보자

내가 1000개의 동전이 든 상자가 있는데 이 중 1개는 앞면만 2개있는 동전이다.
내가 동전을 1개 뽑아서 10번 던졌을 때 모든 결과가 앞면일 때, 이 동전이 앞면만 2개인 동전일 확률은??

이런 문제 상황에서

• 앞면이 2개인 동전일 사건: B
• 앞면이 10번 나올 사건: A

위와 같이 구성을 하자

그러면 문제가 묻는 것은 $P(B|A)$이다.
이를 베이즈로 정리하면
$P(B|A)=\frac{P(A|B)*P(B)}{P(A)}$가 된다.
이를 해결하면 간단하게 풀리는데 $P(A|B)$는 B가 즉 앞면만 2개인 동전이 앞면 10번 나올 확률은 1이고 $P(B)=\frac{1}{1000}$이다.
그리고 $P(A)=P(A|B)*P(B)+P(A|B^c)*P(B^c)$이기에 $P(A)=1*\frac{1}{1000}+\frac{1}{1024}*\frac{999}{1000}$이다
결국 이렇게 값들을 넣으면 $P(B|A)=\frac{1024}{1024+999}$가 된다.
여기에서 재밌는 것은
우리가 처음 생각한 앞면이 2개인 동전이 나올 확률 $P(B)=\frac{1}{1000}$이었다.
그런데 동전을 10번 던져서 앞면이 모두 나온 사건을 관측한 이후 앞면이 2개인 동전이 나올 확률은 $P(B|A)=\frac{1024}{1024+999}\approx0.5...$정도로 절반에 가깝게 매우 상승하였다.

이때 $P(B)$가 우리가 기존에 생각하는 분포 prior이고
$P(B|A)$는 우리가 사건을 관측한 이후에 생각하는 분포 posterior 즉 사후 분포이다.

결론

강화학습에서는 우리는 모든 환경을 100% 알 수 없다.
밴딧 알고리즘과 같이 룰렛을 돌려보면서 점차 확률을 수정해나가는 것이다.
이렇게 기존의 생각인 prior을 특정 사건을 관측한 이후의 상황 posterior로 점차 바꾸어서 점점 정확한 확률로 근사해 나가는 것이다.