링크텍스트
Abstract
이전의 TRPO를 개선한 surrogate objective function을 활용한 gradient ascent optimization을 제시한다.
PPO는 TRPO를 실용적으로 사용할 수 있게 개선한 것이며 minibatch update를 1번만 진행하는 것이 아니라 여러번 진행할 수 있다.
1 Introduction
이 논문은 TRPO를 first-order optimization을 사용해서 간단하게 구현할 수 있으면서 안정적인 성능을 얻는 것이 목적이다.
모델 학습을 위해서 sampling을 진행하고 이를 이용해서 여러번 optimization을 진행한다.
2 Background: Policy Optimization
2.1 Policy Gradient Methods
이전에 다룬 적이 있어서 간단하게 설명하겠다.
기존의 policy gradient에서 gradient를 측정하는 법은 다음과 같다.
g^=E^t[∇θlogπθ(at∣st)A^t]
위 식은 gradient ascent로 진행이 되며 직관적으로 advantage A가 양수이면 즉, 이익을 얻으면 확률을 높이고 A가 낮으면 즉, 손해를 보면 확률을 낮춘다.
여기에서 E^t의 의미는 batch에서 평균을 의미한다.
이를 통해서 sampling과 optimization을 왔다갔다 학습이 가능하다.
그리고 위 gradient는
LPG(θ)=E^t[logπθ(at∣st)A^t].
이 수식을 자동미분으로 학습이 가능하다.
2.2 Trust Region Methods
이전 TRPO 논문에서 마지막에 유도한 공식은 다음과 같다.
maximizeθsubject toE^t[πθold(at∣st)πθ(at∣st)A^t]E^t[KL[πθold(⋅∣st),πθ(⋅∣st)]]≤δ.
여기에서 θold는 update 전의 policy를 의미한다.
그런데 이전 TRPO 논문의 (9) 수식이 다음과 같은데 constraint를 1개의 penalty로 표현이 되어있었다.
η(π~)≥Lπ(π~)−CDKLmax(π,π~),where C=(1−γ)24ϵγ.
이를 활용해서 수식을 다음과 같이 표현이 가능하다.
maximizeθE^t[πθold(at∣st)πθ(at∣st)A^t−βKL[πθold(⋅∣st),πθ(⋅∣st)]]
위 β를 잘 측정하면 특정한 surrogate objective가 lower bound를 구성하게 만들 수 있다. 하지만 TRPO에서는 β를 정하기 너무 어려워서 constraint로 표현을 하고 진행을 하였다.
결국 first-order로 TRPO의 monotonic improvement를 구현하기 위해서는 β를 고르는 것 뿐만 아니라 위 처럼 penalty가 주어진 objective를 최적화하기 위해 추가 수정이 필요하다.
3 Clipped Surrogate Objective
사실상 PPO에서 제일 구현이 간단하고 효과가 좋은 방법이다.
매우 간단한데 위 수식에서 πθold(at∣st)πθ(at∣st)를 rt(θ)로 표현을 하고 시작한다.
그렇기에 r(θold)=1을 만족한다.
이때 우리 의 목적은
LCPI(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t]=E^t[rt(θ)A^t]
이 surrogate objective를 최대화 하는 것이다.
하지만 무작정 constraint나 penalty 없이 update를 진행하게 된다면 policy가 너무 많이 업데이트 되어서 문제가 생기게 된다.
그렇기에 단순히 다른 간단한 방법으로 contraint를 주어서 policy를 조금 업데이트 하면 되지 않을까?
policy가 많이 업데이트 되는 것은 πθold와 πθ가 너무 달라져서 1에서 멀어지는 것이다.
그렇기에 이를 1에서 크게 벗어나지 않게 유지해주는데 다음과 같이 구성한다.
LCLIP(θ)=Et[min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t)]
즉 rt(θ)를 1에서 멀리 벗어나지 않게 1+ϵ과 1−ϵ사이로 clip을 시킨다.
이 논문에서는 ϵ=0.2로 주었다고 한다.
이때 LCLIP와 LCPI는 θold근처에서 first-order가 동일하기에 근사가 가능하다.
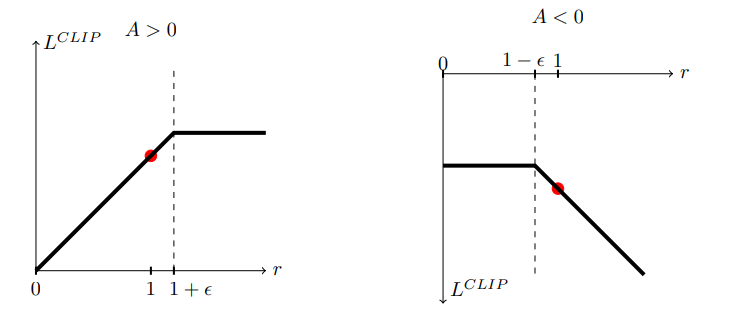
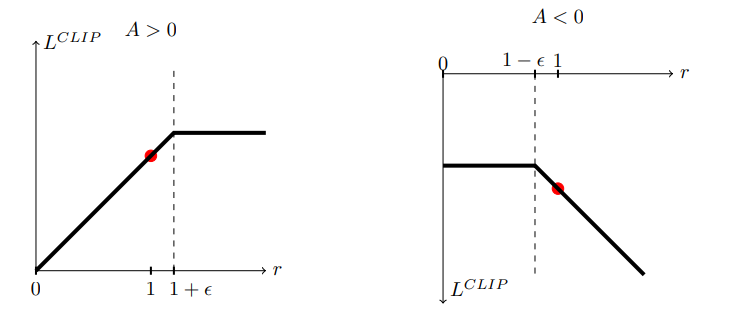
위 그림을 보면 이해가 쉬운데 A>0이면 확률을 늘리는 것이 이득이다. 그러나 1+ϵ 이상으로는 늘리지 않는다.
오른쪽 역시 A<0이면 확률을 줄이는 것이 이득이지만 1−ϵ이하로는 줄이지 않는다. 너무 줄이면 문제가 되기 때문.
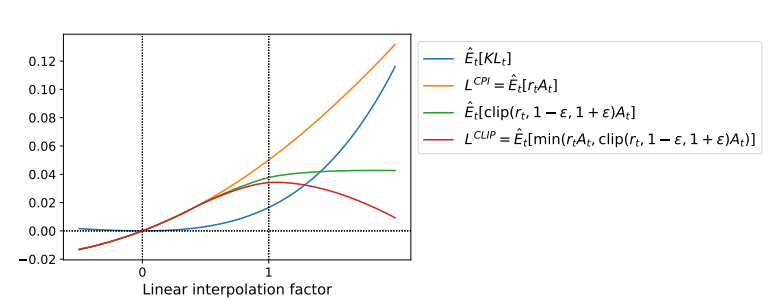 위 그림은 업데이트가 일어나면서 어떻게 각 목적 함수가 변하는지를 보여준다. 0이 처음 θold이다.
위 그림은 업데이트가 일어나면서 어떻게 각 목적 함수가 변하는지를 보여준다. 0이 처음 θold이다.
보면 LCLIP이 LCPI의 lower bound인 것을 알 수 있다.
4 Adaptive KL Penalty Coefficient
사실 위 3번 방식이 실험적으로 좋다고 하고 많이 쓰이지만 우선 논문의 내용이니 이것도 보자
위 내용은 adaptive 즉 적응하는 KL penalty이다.
LKLPEN(θ)=E^t[πθold(at∣st)πθ(at∣st)A^t−βKL[πθold(⋅∣st),πθ(⋅∣st)]]
위와 같은데 사실 기존 수식에서 바뀐게 없다.
대신 β를 하나로 정하는 것이 아니라 유동적으로 바뀌게 한다.
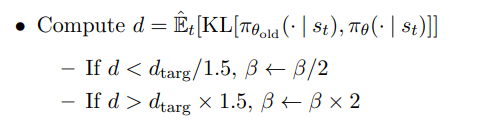 위처럼 penalty Beta가 붙은 값의 결과에 따라서 β의 값을 바꿔준다. 이렇게 업데이트 된 β는 다음 업데이트에 사용이 된다.
위처럼 penalty Beta가 붙은 값의 결과에 따라서 β의 값을 바꿔준다. 이렇게 업데이트 된 β는 다음 업데이트에 사용이 된다.
핵심은 만약 KL divergence가 너무 높았으면 policy가 많이 변했다는 것이기에 β를 키우고 너무 작았으면 policy가 많이 변하지 않았다는 것이기에 β를 줄이는 것이다.
결국 앞의 내용과 비슷하게 policy가 θold에서 크게 벗어나지 않게 penalty의 정도를 조절하는 것이다.
5 Algorithm
앞의 surrogate loss는 자동 미분으로 연산이 가능하기에 구현이 쉽다.
그냥 제일 처음의 LPG대신 쓰면 된다. 그리고 1번 update하고 넘어가는 것이 아니라 한번의 sampling으로 여러번 업데이트가 가능하다.
논문에서 구성한 전체 loss는 CLIP에 value function loss를 더해주고 entropy를 더해줘서 다음과 같이 구성된다.
LtCLIP+VF+S(θ)=E^t[LtCLIP(θ)−c1LtVF(θ)+c2S[πθ](st)]
A^t는 GAE로 계산한다. 추후 글을 작성하겠다.
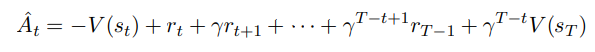
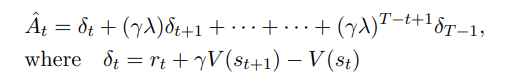
정리하면 다음과 같다.
 N parallel actor이 T timestep을 모은다.
N parallel actor이 T timestep을 모은다.
이후 advantage를 계산하고 surrogate L을 K epoch optimize.
6 Experiments
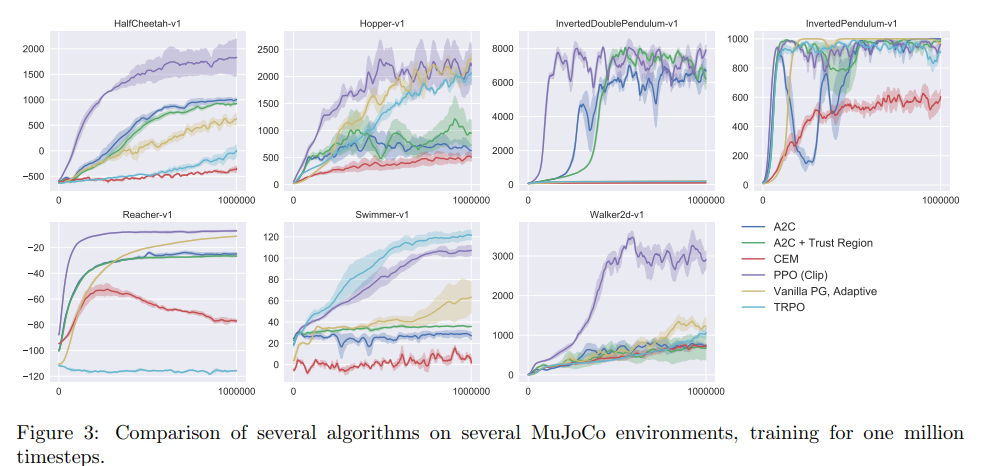

 위 그림은 업데이트가 일어나면서 어떻게 각 목적 함수가 변하는지를 보여준다. 0이 처음 이다.
위 그림은 업데이트가 일어나면서 어떻게 각 목적 함수가 변하는지를 보여준다. 0이 처음 이다.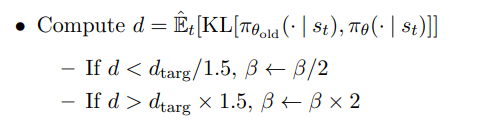 위처럼 penalty Beta가 붙은 값의 결과에 따라서 의 값을 바꿔준다. 이렇게 업데이트 된 는 다음 업데이트에 사용이 된다.
위처럼 penalty Beta가 붙은 값의 결과에 따라서 의 값을 바꿔준다. 이렇게 업데이트 된 는 다음 업데이트에 사용이 된다.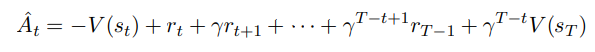
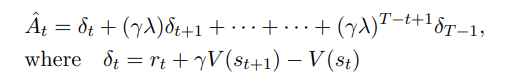
 N parallel actor이 T timestep을 모은다.
N parallel actor이 T timestep을 모은다.
