1. Accuracy (정확도)
-
분류 모델이 전체 데이터셋 중에서 정답을 맞춘 비율을 보여주는 단순 지표
-
만약 데이터가 불균형하다면 (ex. 500개의 데이터 중 490개 데이터 레이블이
0이고 10개 데이터 레이블이1이면 모델이 예측을0으로 하면 accuracy가 98%) 이진분류 (Binary Classification)에서는 모델의 성능이 왜곡 될 수도 있음. -
따라서 분류 성능 평가에서는 Accuracy보다 다른 성능 지표들을 사용하여 모델의 성능을 평가
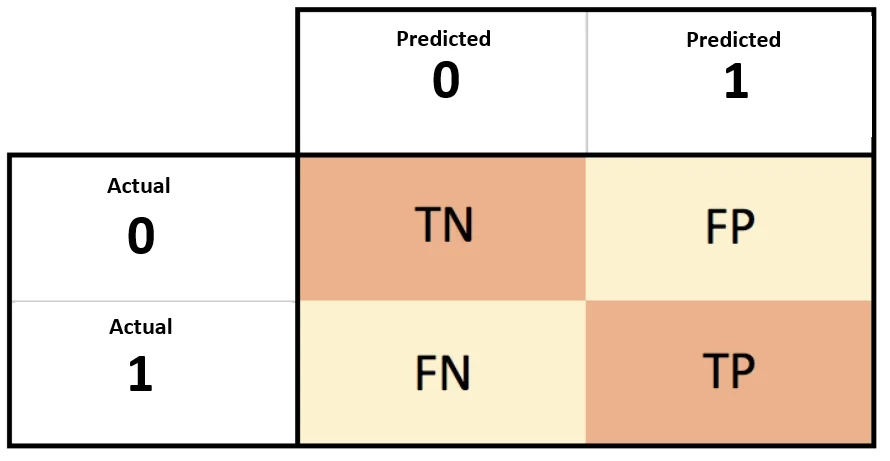
2. Confusion Matrix (혼동 행렬, 오차 행렬)
-
분류 모델의 성능을 측정하는데 자주 사용되는 행렬
-
예측 오류가 얼마인지와 어떠한 유형의 예측 오류가 발생하는지를 한눈에 알 수 있는 지표
🔹 TRUE : 정답
🔹 FALSE : 오답
🔹 Positive : 분류 모델이 positive라고 예측
🔹 Negative : 분류 모델이 negative라고 예측💡 TP (True Positive) : 모델이 positive라고 예측 / 실제 정답이 positive (정답)
💡 FP (False Positive) : 모델이 positive라고 예측 / 실제 정답이 negative (오답)
💡 TN (True Negative) : 모델이 negative라고 예측 / 실제 정답이 negative (정답)
💡 FN (False Negative) : 모델이 negative라고 예측 / 실제 정답이 positive (오답)⭐️ 불균형한 데이터셋에서는 중점적을 찾아야 하는 레이블에 1, 그렇지 않은 경우에는 0을 부여
1. Accuracy (정확도)
- 전체 데이터셋 중 정답을 맞춘 비율
2. Precision (정밀도)
-
모델이 positive라고 예측한 데이터 중에서 실제로 정답이 positive인 비율
-
Precision을 높이기 위해서는 FP를 낮추는 것이 중요
-
0~1사이의 값을 가지며, 1에 가까울수록 좋음
3. Recall (재현율)
-
True Positive Rate (TPR / 민감도)라고도 부름
-
실제 정답이 positive인 데이터 중에서 모델이 positive라고 예측한 비율
-
Recall을 높이기 위해선 FN을 낮추는 것이 중요
-
Precision과 마찬가지로 0~1사이의 값을 가지며, 1에 가까울수록 좋음
⭐️ Precision과 Recall 모두 TP를 높이는 것에 초점을 두지만, Precision은 FP를 낮추는데, Recall은 FN을 낮추는 것에 초점을 둠.
⭐️ Recall이 Precision보다 상대적으로 중요함
⭐️ 암 검출, 금융사기 검출 모델에서는 실제 positive인(암, 금융사기)것을 negative로 예측하면 모델의 정확성이 좋지 않음 → Recall이 중요
⭐️ 스팸 검출 모델에서는 실제 negative(스팸x)를 positive로 예측하면 모델의 정확성이 좋지 않음 → Precision이 중요
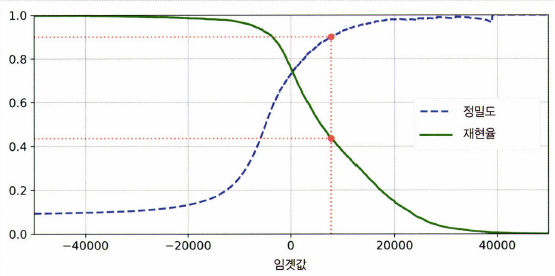
4. Precision/Recall Trade-off
-
Precision과 Recall은 상호 보완적인 평가 지표이므로 어느 한쪽을 높이게 되면 다른 하나의 수치는 떨어질 수 있음
-
따라서 Precision과 Recall의 Trade-off를 결정하는 값을 Decision Threshold라고 함 (Positive 예측값을 결정하는 확률의 기준)
-
이진 분류일 때 확률이 0.5 초과면 Positive, 0.5보다 작으면 Negative라고 예측
-
Decision Threshold를 낮추면 (0.5보다 작은 값) Positive로 예측하는 값이 많아지므로 Precision ↓, Recall ↑
-
Decision Threshold를 높이면 (0.5보다 큰 값) Positive로 예측하는 값이 적어지므로 Precision ↑, Recall ↓
5. F1 Score
-
Recall과 Precision의 조화평균
-
위에서 적었듯이 Recall과 Precision은 Trade-off 관계이므로 F1 Score를 사용
-
Precision과 Recall이 어느 한쪽으로 치우치치 않을 때 높은 값을 가짐
6. 기타 지표들
1. Error Rate
- 모델이 전체 데이터에서 오답을 예측한 비율
2. Specificity (특이성)
-
True Negative Rate(TNR)라고도 부름
-
실제 정답이 Negative인것들 중에서 모델이 Negative라고 예측한 비율
3. Fall Out (위양성률)
-
False Positive Rate(FPR) 라고도 부름
-
실제 정답이 Negative인것들 중에서 모델이 Positive라고 예측한 비율
3. ROC Curve
-
False Positive Rate(FPR)이 변할 때 True Positive Rate(TPR)이 어떻게 변하는지를 나타내는 곡선
-
FPR을
x축, TPR를y축으로 잡은 그래프
➰ FPR은1-TNR➰ TPR은
Recall과 같은 개념
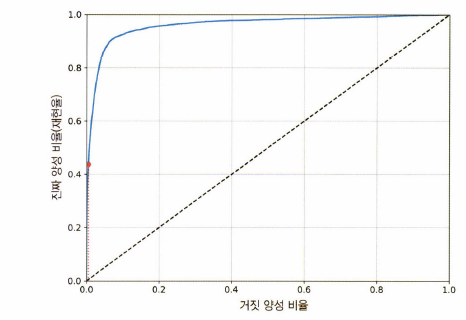
- ROC Curve에 있는 직선에 가까울수록 성능이 떨어짐, 되도록 멀어야함
⭐️ AUC Score
- ROC Curve를 가지고 실제 사용하는 성능 지표는 ROC Curve의 면적인 AUC값
- ROC Curve에서 직선에서 멀수록 성능이 좋은 것이므로 AUC가 1에 가까울수록 성능이 좋은 것
Reference
https://driip.me/3ef36050-f5a3-41ea-9f23-874afe665342
https://white-joy.tistory.com/9?category=1015070
