
Codiility Stone Wall 코딜리티
O(n)으로 loop를 돌면서 개수를 세는 문제는 흔하지만, 코딜리티의 이 문제가 도형 높이, 채워지는 물의 부피 등을 계산할 때 기본이 될 수 있는 문제라 생각하여 포스팅해둔다. 기본적이면서 매우 좋은 문제라 생각.
Question

H:List가 주어졌을 때 각 element: int 들은 H[i] -> i~i+1 까지 벽의 높이를 뜻한다. 주어진 벽 모양을 직사각형으로 채울 때 가능한 최소의 직사각형 수는?
Solution
-
높이가 같다면? 새롭게 사각형을 추가하지 않아도 되므로 그냥 continue
-
높이가 증가한다면? stack에 숫자를 추가해둠 (그렇다면 서로 다른 높이들이 들어있게 되겠지)
-
높이가 감소한다면? 감소한 높이(H[i])로 stack에 들어있는 앞쪽 벽 높이 중 더 높은 벽들을 다 잘라낸다. 생각해보면 H[i]보다 높은 3가지 높이가 들어 있다고 한다면 3가지는 3개의 사각형으로 채울 수밖에 없다. 즉, stack에서 꺼내는 숫자만큼 ans += 1.
그리고 위쪽을 잘라냈다는 것은 잘라낸 부분 만큼은 새로운 높이(H[i])가 가장 높은 높이가 되는 것이므로.. 새로운 높이를 stack에 추가. (이 때 stack[-1]과 같다면 굳이 추가할 필요가 없다) -
마지막에 stack에 숫자들이 남아있다면 그 만큼의 각각 다른 높이들이 남아있는 것이기 때문에 그 개수만큼의 사각형으로 채워야 하므로, ans에 stack의 길이만큼 더해준다.
-
코드 상으로는 stack 처음에 0을 추가해서 예외 없이 일관된 loop가 돌아갈 수 있도록 했다.
그림을 그려서 이해해보면 좋겠다.
재미있게 풀었던 문제라서 그림을 그려보았다. 예시인 [8,8,5,7,9,8,7,4,8]의 경우이다.
높이가 감소할 경우, 낮은 높이로 자르면 윗 부분은 직사각형이 하나 생긴다.
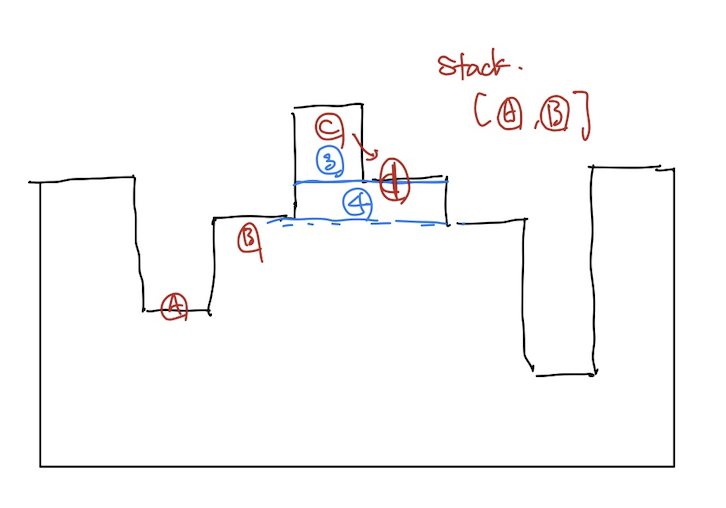
높이가 증가할 때는 stack에 높이를 추가해둔다. [A,B,C]까지 stack에 들어간다. 그리고 D가 등장하면서 높이는 감소. D높이로 자른다고 생각해보자. 그럼 D보다 높은 곳들은 사각형으로 잘리게 되는데, 여기서는 우선 C만 D보다 높기 때문에 하나의 사각형만 추가되게 된다.(3번 사각형)
그렇다면 이제 안 잘리고 남은 높이는 [A,B,D]로 바뀌게 된다.
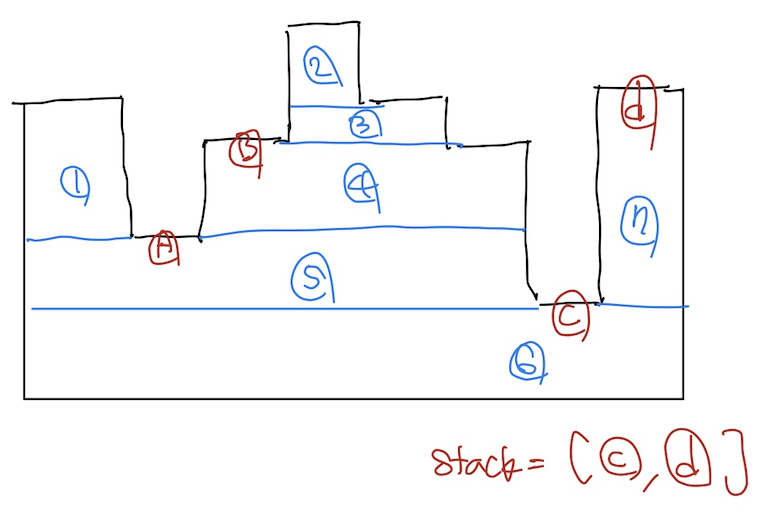
아래 그림에서 새로운 낮은 높이 C가 등장했다. C보다 높은 높이는 A와 B가 stack에 남아있을 텐데, C보다 높은 높이들을 하나씩 pop() 해주면서 새로운 사각형이 하나씩 생긴다.
그러고 나면 남은 높이(stack)는 C 하나가 되며 D는 증가 부분이기 때문에 규칙대로 stack에 그대로 추가한다. 모든 loop이 돌고 나면 pop() 했던 횟수인 5와 stack에는 [C, D]가 남게 되는 것이다. 둘의 높이가 다르니 추가로 사각형 두 개가 더 필요할 것이다.
다른 방식으로 자를 수도 있겠지만 나는 이렇게 이해하는 편이 편했다.
def solution(H):
ans = 0
stack = [0]
for val in H:
if val == stack[-1]:
continue
if val > stack[-1]:
stack.append(val)
else:
while stack[-1] > val:
stack.pop()
ans += 1
if stack[-1] != val:
stack.append(val)
ans += (len(stack)-1)
return ans