[boj3944] int(digits, n). n진법 수 변환하기

boj3944 나머지 계산 백준 3944

Question

예시) 7진법 123456이 주어졌을 때 이 수를 6으로 나눴을 때의 나머지를 출력한다.

Solution

Solution 1: n진법의 원리

10진법 782는 100*7 + 10*8 + 1*2 로 쓸 수 있다. 이는 다시 (99*7 + 1*7) + (9*8 + 1*8) + (1*2)로 나눠서 표현할 수 있다. n-1인 9로 나눈다고 생각해보면 각 자리수에서 1*k만 남게 되는 것을 알 수 있다. 즉, 단순하게 모든 자리의 숫자를 더해준 값을 다시 n-1로 나눠서 나오는 나머지가 전체 수의 나머지와 같다는 것이다.
각 자리수의 값들을 더해줄 때 loop을 돌거나 sum() 함수를 이용할 수 있는데, loop을 돌았더니 시간 초과가 나오더라.. sum() 또한 O(n)에 가깝게 구현이 될 텐데 내장함수가 직접 구현하는 것보다 빠른 경우가 많은 듯하다. 둘의 구동 시간 비교는 글 아래 결과에 있다.

def sol_1(n:int, digits: str) -> int:
    cum = 0
    for i in digits:
        cum += int(i)
    return cum % (n-1)

def sol_2(n:int, digits: str) -> int:
    return sum(map(int, list(digits))) % (n-1)

Solution 2: int() 활용

int() 함수는 주로 아래처럼 str type의 digit를 int type으로 변경할 때 사용한다. 단지 타입 변환 느낌으로만 알고 있었다. 그런데 아래 이미지처럼 n진법의 수를 인식할 때에도 int()가 유용하다. '1101011'이라는 2진법 형태의 str을 10진법 int 형태로 변환했을 때 107이 나온다는 뜻이다.

int('35')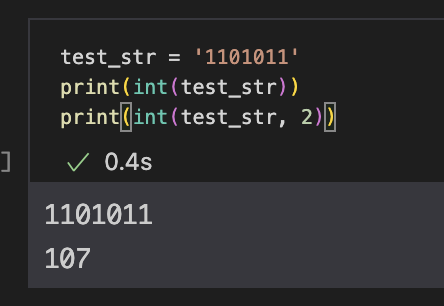

그렇다면 아래와 같이 간단하게 n진법의 수를 int() (10진법)으로 읽은 후 (n-1)로 나눠준 나머지를 출력하면 끝.

def sol_3(n:int, digits: str) -> int:
    return int(digits, n) % (n-1)

결과

아래의 시간초과는 Solution1 방식 중 직접 loop을 돌면서 sum 값을 얻어내는 방식으로 풀었을 때, 위의 둘은 Solution2의 방식으로 풀었을 때이다. IDE 상에서 실행했을 때에는 Solution2가 가장 빠른데, 백준에서는 계속 시간초과가 나왔던 점이 의아했다. 다른 문제가 있는 건가?

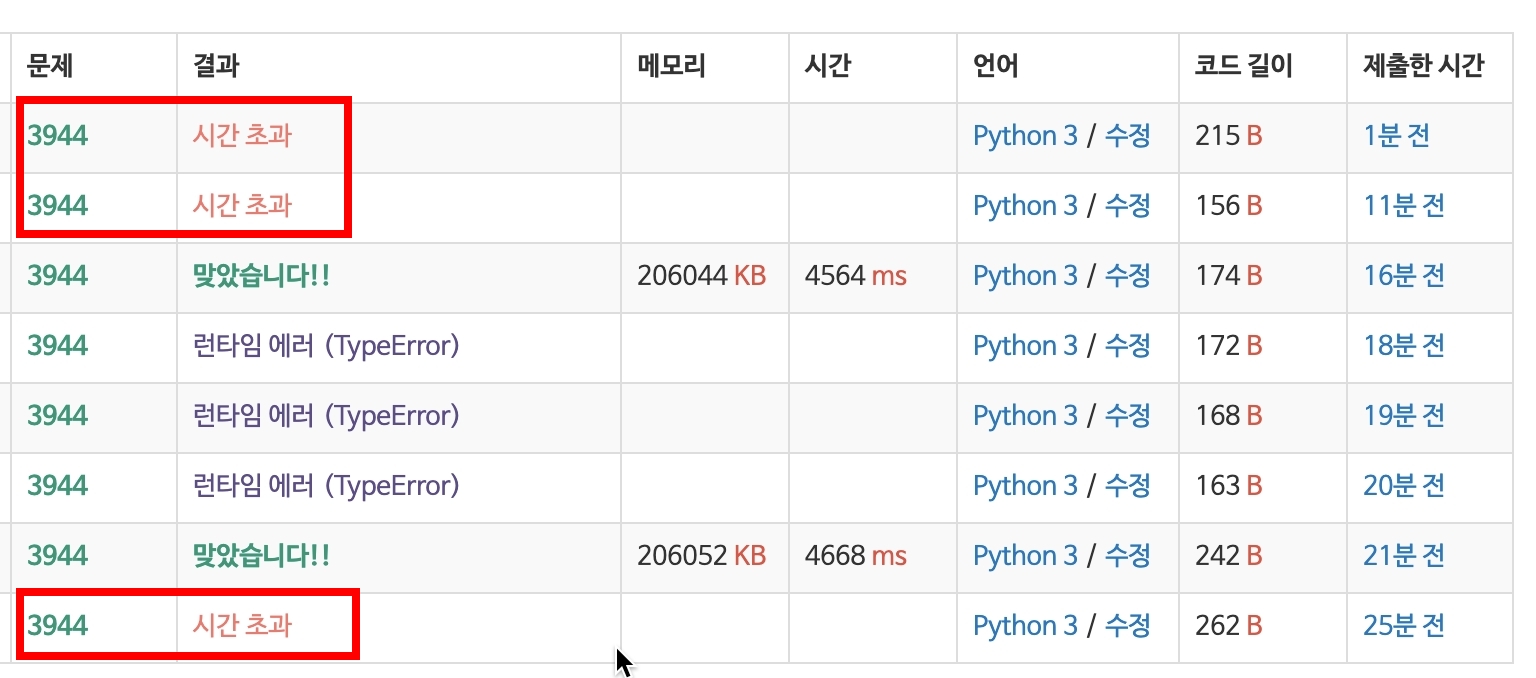
이미지처럼 세 번째(solution 2)가 항상 가장 빨랐다.