[leet32]가장 긴 괄호 찾기. 다이나믹 프로그래밍

leetcode 32 longest valid parenthesis

Dynamic Programming이란?

내가 이해하기로는 중간 중간 과정을 기록하고(dict나 dp list 등을 만들어서), 새로운 문제가 주어졌을 때 기존에 진행했던 코드와 기록해두었던 결과를 바탕으로 그 상황을 시작점으로 삼아 문제를 풀어가는 것이다.

피보나치 수열을 구할 때를 생각해보자.
f(3) = f(2) + f(1), f(4) = f(3) + f(2) 이기 때문에 f(2) 값을 두차례 계산해야 한다. 반면 f(2) 값을 앞에서 한 번 구한 후 dict에 저장해둔다면, f(4)에서는 단순히 O(1)로 dict를 탐색하고 그대로 사용하면 될 것이다. 이처럼 기존 계산 결과들을 기억해뒀다가 다음 계산에 활용해볼 수 있도록 솔루션을 짜는 걸 DP라 한다. (혹시 더 직관적이고 이해가 빠를 설명이 있다면 댓글 부탁드립니다)

Question

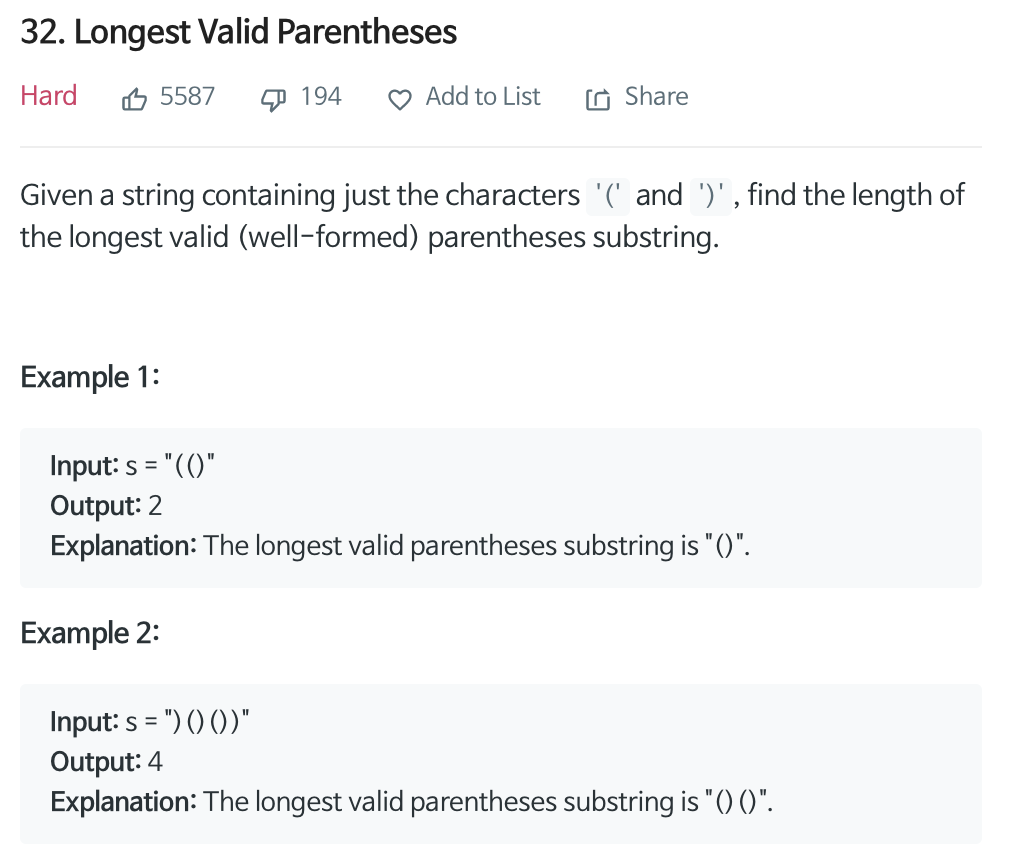
Longest Valid Parenthesis
()로 이뤄진 주어진 string 내에서 유효한 substring 중 가장 긴 것의 길이를 찾아라

Solution

Solution 1

우선 모든 가능한 케이스들을 valid한지 확인하며 max_len을 업데이트하는 방식으로 진행해보았다. 최대한 케이스를 줄여가며 진행했으나 시간초과.

PSEUDO

• isValid 정의: s가 유효한 괄호인지?
• for i in range(0, len(s)-1):
  for j in range(i+1, len(s), 2): # 이 부분에서 가능 케이스를 줄이기 위해 2 단위로 건너가도록!
  s[i:j+1]이 isValid인지 확인
  맞다면 max_len 업데이트

Solution 2

위 방식은 한번 확인한 substring들을 다시 확인하게 된다. s[3:5]가 valid 하다는 점을 s[1:5]를 체크할 때 알게 됐는데, s[3:7]을 체크할 때 다시 확인해야하기 때문이다.
그래서 중간중간의 결과를 기록해두고 다음에 사용할 수 있는 Dynamic Programming 방식을 도입해본다.

PSEUDO

• dp = [0] * length
• )이 나왔을 때, s[i-1]이 ( 이면, dp[i] = dp[i-2] +2. # 길이 2짜리 유효한 괄호가 추가
• )이 나왔을 때, s[i-1] == ) 라면 + dp[i-1] != 0 (바로 앞까지 유효한 괄호였다면)
  i-dp[i-1]-1이 열리는 괄호인지 확인해야 함(=바로 앞 유효 괄호 세트보다 하나 더 앞에서 열리고, i에서 닫히는지)
  그렇다면 dp[i-1]+2로 진행 중이던 괄호를 늘려주고, dp[i-dp[i-1]-2]를 더해줘야 함. (=그 앞에서 진행되던 유효괄호가 있다면 더해줘야)
• return max(dp)

code

def sol_1(s):
    'is valid'
    def isValid(str_):
        open_ = 0
        for char in str_:
            if char == '(':
                open_ += 1
            else:
                if not open_:
                    return False
                open_ -= 1
        return open_ == 0
    
    max_len = 0
    for i in range(len(s)-1):
        for j in range(i+1, len(s), 2):
            if isValid(s[i:j+1]):
                max_len = max(max_len, j+1-i)
    return max_len코드를 입력하세요

def sol_2(s):
    'dynamic promgramming'
    n = len(s)
    if n <= 1:
        return 0
    dp = [0]*n # [0,0,0,0,0]

    for i in range(1, n):
        if s[i] == ')':
            if s[i-1] == '(':
                dp[i] = dp[i-2] + 2 # + '()'
            else: # '))
                before = dp[i-1]
                if before and (i -before-1 >= 0) and s[i-before-1] == '(': # before == 0 인 경우에는 s[i-before-1]=='('가 성립하지 못함. 
                    dp[i] = dp[i-1] + 2 + dp[i-before-2] # i-before-2 == -1이 되면 0 값이 되기 때문에 상관 없음
    return max(dp)

time limit 초과로 통과하지 못했던 Solution 1과 통과 가능했던 Solution 2

github link