leetcode 34 Find first and last position of element in sorted array
Binary Search
Array에서 target을 찾는 일을 생각해보자. 일반적으로는 Linear Search를 할 것이다. 0번 idx부터 -1번 idx까지 돌면서 맞니? 확인하게 된다. time은 당연히 O(n). m개의 target을 찾는 작업을 수행한다면 O(n*m)이 된다. m>n일 때에는 O(n^2) 이상이 되는 것이다.
Array가 [1,2,3,4,5,6,7,8,9,10]라 생각해보자.
- Ascending order로 정렬되어 있다.
- mid 값(5나 6)을 추출해서 target인 3과 비교해본다.
- mid보다 target이 작기 때문에 mid의 왼쪽 부분만 같은 방식으로 다시 찾는다. (recursion)
계속 대상을 반으로 쪼개어 찾기 때문에 O(log_2 N)으로 이뤄지게 된다. (== O(log n))
아래는 정렬된 array에서 8을 찾아가는 예시. mid=6을 기준으로 오른쪽 array를 다시 Binary Search. 이후도 마찬가지로 mid=9 기준으로 왼쪽을 Search.
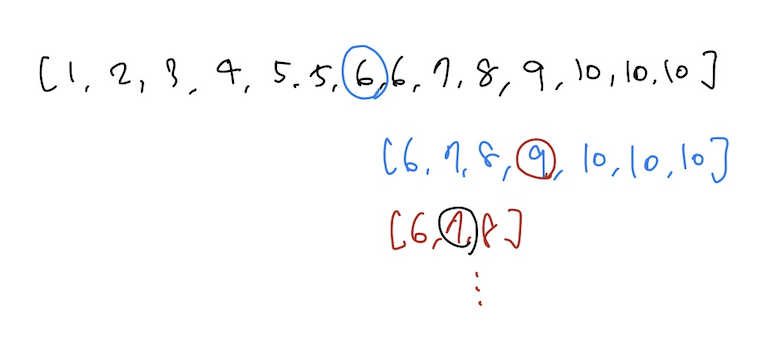
무엇이 더 좋은 방식인가?
- 정렬이 되어 있다면 Binary Search가 당연히 좋다.
- 정렬이 안 되어 있다면 정렬하는 과정이 필요하기 때문에 기본적으로는 Binary Search가 느리다.
- 다만 여러 차례 search를 수행해야 한다면 한번 정렬 후 더 빠른 Binary Search로 탐색하는 편이 빠르다.
Question

- 핵심은 O(log n)으로 풀어볼 것! -> Linear Search를 사용하지 말 것
Solution
Solution 1
PSEUDO
BS로 target_idx를 하나 찾은 다음 앞뒤로 같은 값이 나오는 부분까지 search하기
O(log n)으로 target을 찾은 후에 왼쪽 오른쪽으로 linear search가 이뤄지기 때문에 만약 target값이 양끝까지 모두 분포한다면 O(log n) + O(n)이 되어 O(n)이 될 수 있다. (최악의 경우엔 조건에 어긋날 수 있다)
def sol_1(nums, target):
if not nums: return [-1, -1]
def bs(list1, start, end, target):
if start > end: return -1
if start == end and list1[start] == target:
return start
mid = (start + end+1)//2
if list1[mid] == target: return mid
elif list1[mid] > target:
return bs(list1, start, mid-1, target)
else:
return bs(list1, mid+1, end, target)
target_idx = bs(nums, 0, len(nums)-1, target)
if target_idx == -1: return [-1, -1]
left, right = target_idx, target_idx
while right < len(nums):
if nums[right] != target:
break
right += 1
while left >= 0:
if nums[left] != target:
break
left -= 1
return [left+1, right-1]Solution 2
BS로 left, right idx를 각각 찾음
left: 가장 앞 target_idx
right: 가장 뒤 target_idx
각각 O(log n)으로 이뤄지기 때문에 전체 time도 O(log n). (조건에 부합)
PSEUDO
- right 찾기
- l, r을 0, len(list)-1로 초기화하고
- mid로 target을 찾는다면 -> 오른쪽으로 계속 target을 찾아가서 right 값 찾기
- 똑같이 l, r을 초기화 후 left 값 찾기
def sol_2(nums, target):
l, r = 0, len(nums)-1
first = last = -1
while l <= r:
m = (l+r)//2
if nums[m] == target:
first = m
r = m-1
elif nums[m] > target:
r = m-1
elif nums[m] < target:
l = m+1
l, r = 0, len(nums)-1
while l <= r:
m = (l+r)//2
if nums[m] == target:
last = m
l = m+1
elif nums[m] > target:
r = m-1
elif nums[m] < target:
l = m+1
return [first, last]Solution 1과 2의 속도 비교. 2가 빠르며 큰 속도차이는 나지 않는 듯하다. 하지만 Leetcode의 test case에서는 Sol 1도 빠른 속도로 통과 가능. (마지막 이미지)