[boj2579][leet55] 다이나믹 프로그래밍 기본 문제

Dynamic Programing

DP에 대해서는 앞서도 몇 차례 다룬 바 있다. 첫번째 글(Link)에서 아래와 같은 느낌으로 모호하게 이해하고 있었는데 문제를 풀어가면서 조금씩 뚜렷하게 이해가 되는 느낌이다.

내가 이해하기로는 중간 중간 과정을 기록하고(dict나 dp list 등을 만들어서), 새로운 문제가 주어졌을 때 기존에 진행했던 코드와 기록해두었던 결과를 바탕으로 그 상황을 시작점으로 삼아 문제를 풀어가는 것이다.

점화식으로 풀어가는 느낌. i번째 값을 구할 때, i-1, i-2 등의 값들을 저장해두었다가 사용하는 것이다. 각각의 관계를 명확하게 정의해준다면 쉽게 답을 얻을 수 있다. 아래 두 가지 베이직 문제들을 보면서 이해해보길.

Question

Dynamic Programing으로 접근 가능한 두 가지 기본 문제이다.

Question 1. BOJ2579 계단오르기

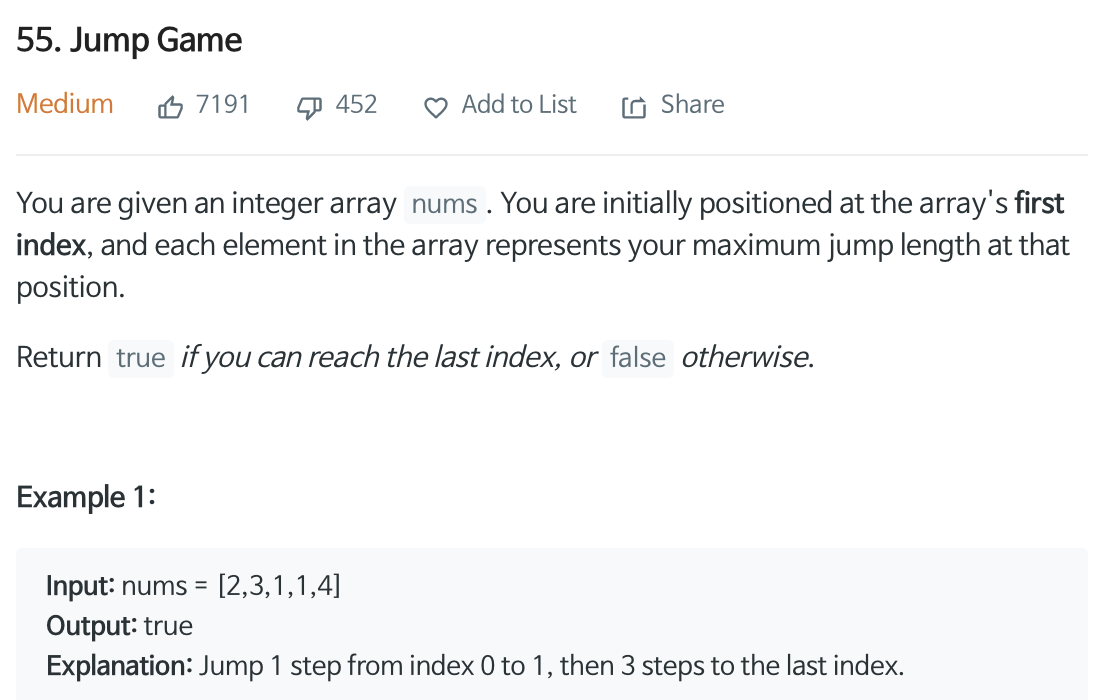
Question 2. leetcode55 Jump Game

Solution

Question 1.

DP list에 그 계단에서 가능한 max값을 담는다. 아래 두 가지 케이스의 값들을 구하고 둘 중 큰 값을 담으면 된다.

• 한 칸을 뛰어올라온 경우: 그 이전에도 한 칸을 뛰어올랐을 경우를 배제해야 하기 때문에(연속 3칸 밟기 불가능) 세 계단 이전까지의 max 값(dp[i-3]) + 두 계단 이전의 값(nums[i-2]) + 현재 계단의 값(nums[i])이 된다.

• 두 칸을 뛰어올라온 경우: 두 계단 전에 도달할 때는 앞서 두 계단이든 한 계단이든 상관이 없기 때문에 두 계단 이전까지의 최대값(dp[i-2]) + 현재 계단의 값(nums[i])이 된다.

def sol(nums):
    if len(nums) == 1: return nums[0]
    if len(nums) == 2: return sum(nums)
    dp = [0 for _ in range(len(nums))]
    dp[0] = nums[0]
    dp[1] = dp[0] + nums[1]
    dp[2] = max(dp[0]+nums[2], nums[1]+nums[2]) # [10, 30, 35]

    for idx in range(3, len(nums)):
        dp[idx] = max((dp[idx-3]+nums[idx-1]+nums[idx]), (dp[idx-2]+nums[idx]))
    return dp[-1]

Question 2.

Sol 2.가 DP로 접근한 방식이다. DP list에는 그 이전까지의 값들로 갈 수 있는 가장 큰 index가 담긴다. 따라서 만약 dp[i-1]보다 i가 커지게 된다면 그 자리는 갈 수 없는 자리가 되기 때문에 바로 False를 return 할 수 있다.
dp[i]에는 i-1번째까지 기준으로 갈 수 있는 가장 큰 index와 i번째(i번째도 도달 가능하므로) 값 기준으로 도달할 수 있는 가장 큰 index를 비교해 큰 값이 배정되게 된다. (점화식)

def sol_1(nums: List[int]) -> bool:
    max_idx = 0
    i = 0
    while i < len(nums):
        max_idx = max(max_idx, i+nums[i])
        if max_idx >= len(nums)-1: return True
        i += 1
        if i > max_idx: return False

def sol_2(nums) -> bool:
    length = len(nums)
    dp = [0 for _ in range(length)]
    dp[0] = nums[0]

    for i in range(1, length):
        if i > dp[i-1]: return False
        dp[i] = max(dp[i-1], i+nums[i])
        if dp[i] >= length-1: return True

Q1 github
Q2 github