
leetcode 67 add binary
zip과 zip_longest
여러 data들을 iterator로 만들어서 동시에 iteration을 진행할 때 사용한다. zip은 길이가 같은 데이터들을 묶어줄 때 사용하며, zip_longest는 데이터들의 길이가 각각 다를 때 가장 긴 데이터를 기준으로 나머지 데이터들의 길이를 맞춰준다. 학습을 위한 Dataset을 만들 때나 모델 안에서 iteration을 돌 때도 zip을 자주 사용하니 알아두면 좋겠다.
a = '1111010'
b = '1234567'
c = '98765'
for i, j in zip(a, b):
print(i, j)
for i, j in zip(a, c):
print(i, j)
for i, j in zip_longest(a, c, fillvalue='0'):
print(i, j)첫 번째는 길이가 같기 때문에 7자리가 하나씩 출력된다.
두 번째는 길이가 다른데 짧은 데이터에 맞춰서 iteration이 돈다. 즉 a는 '11110'까지만 출력된다.
세 번째는 길이가 긴 a에 맞춰서 출력되는데 부족한 자리는 '0'을 채워준다. 즉 c는 '9876500'이 된다.

Question
문제는 간단하다. 이진법으로 표기된 두 수(str)의 합을 이진법(str)으로 나타내라.

Solution
두 가지 방법이 있다. 하나는 이진법 상태에서 덧셈을 하는 것이고 나머지는 십진수로 바꾸어서 덧셈 후 다시 이진수로 표기하는 것이다. 아래 Solution 1,2는 첫 번째 방식이고 3이 두 번째 방식이다.
Solution 1
두 숫자를 뒤집는다.
끝자리부터 덧셈을 한다. 우리가 덧셈을 할 때 쓰는 '올림' 이라는 걸 적용한다. 2가 넘어갈 때는 1을 올려주고 현재 자리수에는 2를 뺀 숫자를 넣는다. (더해서 14가 된다면 4만 그 자리에 넣고 10은 위로 1 올려주는 것처럼)
이 과정을 a, b에 모두 존재하는 자리수들에서 해주다가 한쪽이 끝나면 다른 한쪽만을 대상으로 끝까지 진행한다. 11000, 101 이라면 3자리까지는 같이 덧셈을 진행하다가 101이 끝났기 때문에 남은 11000에서 11 부분을 대상으로 진행하는 것이다. 아래와 같이 진행 후 while a_i < len(a) 와 while b_i < len(b)를 각각 진행해주면 된다.
while a_i < len(a) and b_i < len(b):
temp = int(a[a_i]) + int(b[b_i]) + up
up = 0
if temp >= 2:
up += 1
temp -= 2
ans += str(temp)
a_i += 1
b_i += 1
Solution 2
같은 방식이지만 itertools.zip_longest를 사용해서 같은 자리수를 가진 숫자로 만들어놓고 진행한다. 별도의 while문이 없어도 되기 때문에 코드가 매우 간단해진다.
def sol_2(a:str, b:str) -> str:
a, b = a[::-1], b[::-1]
ans = str()
up = 0
for val1, val2 in zip_longest(a,b, fillvalue='0'):
up, present = divmod((int(val1) + int(val2) + up), 2)
ans += str(present)
if up: ans += '1'
return ans[::-1]Solution 3
두 수를 십진법으로 바꾼 후 덧셈, 그리고 다시 이진법으로 변환하여 return 한다. 이진법 표기 -> 십진법 표기, 십진법 표기 -> 이진법 표기 방식을 간단하게 할 수 있도록 이해해두면 좋다.
이진법을 십진법으로 바꿔줄 때는 끝자리부터 2**n을 곱해서 더해가면 된다. 아래 to_ten을 보면 이해가 쉽다.
십진법을 이진법으로 바꿔줄 때는 어렸을 때 배웠던 이진법 표기 방법을 떠올려 보면 된다. 2로 나눠가면서 나머지를 끝자리(작은 자리수)부터 채워간다.

def to_ten(s: str):
ans = 0
n = 0
for char in s[::-1]:
ans += int(char) * (2**n)
n += 1
return ans
def to_binary(val: int) -> str:
if val == 0: return '0'
ans = str()
while val != 0:
val, v2 = divmod(val, 2)
ans += str(v2)
return ans[::-1]
업데이트! 2진법과 10진법 편하게 변경 가능한 방법
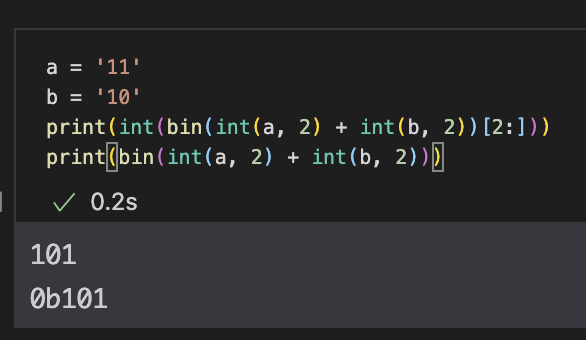
str type의 이진수를 int()로 인식하면서 2를 같이 주면 10진수로 변환하여 int type으로 반환된다. 덧뺄셈 후 다시 bin()에 넣어주면 str type의 이진수로 변환되는데 앞에 0b가 붙는다. 그 부분만 잘라서 return하면 끝.
