[leet152] DP로 Subarray 구하기(Kadane's Algorithm)

leetcode 53 Maximum Subarray
leetcode 152 Maximum Product Subarray

Kadane's Algorithm

다이나믹 프로그래밍의 일종이다. 특정 조건에 맞는 Subarray를 구하고자 할 때 사용하기 좋다.
아래 nums list가 있다고 하자. dp[2]는 2번 원소를 마지막 index에 포함하고 있는 subarray 중 가장 큰 합을 갖는 subarray의 합이다. 예를 들어, [1,2]가 maximum subarray가 된다고 표기했다.
dp[3]을 구할 때를 생각해보면, 2번 원소를 포함하는 세 개의 subarray 뒤에 3을 append 해주는 경우가 있을 것이고, 새롭게 3만을 원소로 갖는 subarray가 있을 것이다. 당연하게도 전자의 경우엔 dp[2]의 값에 3을 더해준 값이 최대값이 된다. 그래서 dp[2]+nums[3]과 nums[3] 중 큰 값이 dp[3], 즉 3번 원소를 마지막 자리에 포함하는 subarray가 가질 수 있는 sum 값 중 가장 큰 값이 된다.

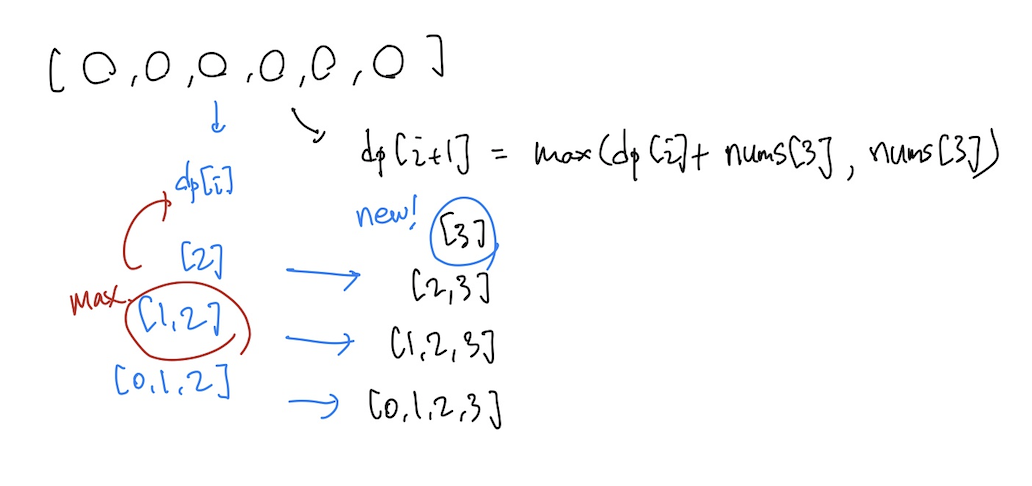
설명이 정말정말 잘 돼 있는 게시물을 참고해보자 -> Link

Question

Subarray 중 최대의 합을 갖는 것을 구하는 문제와 최대의 곱을 구하는 문제이다.

Question 1: leet53. Maximum Sum

Question 2: leet152. Maximum Product

Solution

Solution (Q1)

합을 구하기 때문에 dp[i-1]을 기준으로 dp[i]의 max 값을 계속 구해가면 된다.

def sol_1(nums):
    global_max = nums[0]
    local_max = nums[0]

    for idx in range(1, len(nums)):
        local_max = max(local_max+nums[idx], nums[idx])
        global_max = max(global_max, local_max)
    return global_max

Solution (Q2)

곱을 구할 때는 정수 부호를 따져야 한다. nums[i]가 양수일 때는 dp[i-1]의 maximum에 nums[i]를 곱해줘야 하고, 음수일 때는 dp[i-1]의 minimum에 곱해줘야 한다.

def sol_2(nums):
    cur_max, cur_min, g_max = nums[0], nums[0], nums[0]
    for i in range(1, len(nums)):
        if nums[i] >= 0:
            cur_max, cur_min = max(cur_max*nums[i], nums[i]), min(cur_min*nums[i], nums[i])
        else:
            cur_max, cur_min = max(cur_min*nums[i], nums[i]), min(cur_max*nums[i], nums[i])
        g_max = max(g_max, cur_max)
    return g_max

github