[pgs큰 수 만들기] Greedy 알고리즘과 Stack

프로그래머스 큰 수 만들기
중복되는 연산을 줄이자..

Greedy algorithm

각 시점에서 최고의 선택을 한다. 이런 부분 선택들이 모이다 보면 전체로도 최적의 선택이 된다. (=문제를 쪼개서 하나씩 풀어가는 느낌이다)
수업을 많이 들을 수 있도록 시간표를 짜는 문제에서 앞에서부터 항상 가장 종료시간이 빠른 강의들로 채워나가거나, 아래처럼 큰 수를 만들어갈 때 앞에서부터 가장 큰 digit들을 남기고 그 앞의 숫자들은 제거간다거나. 이런 method들이 계속 반복해서 적용될 수 있는 알고리즘을 말한다.
사실 알고리즘은 이렇게 이해하는 것보다 문제들을 접하면서 이해하는 게 낫더라...

Question

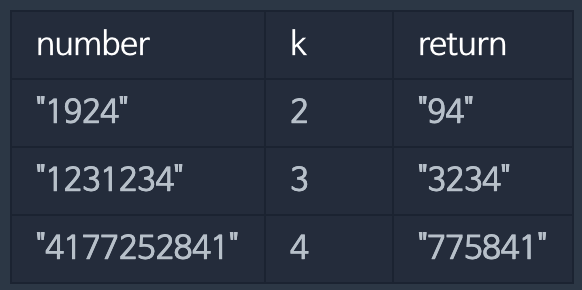
Solution

Solution 1

Greedy 방식의 일부로 아래와 같은 메소드를 만들고 k가 남아있을 때까지 반복 수행한다.
항상 앞에서 k+1 개의 숫자 중 가장 큰 숫자를 뽑아내고
1) 그 앞 숫자들은 날린다. k-=날린 숫자 개수
2) 가장 큰 숫자는 ans에 붙인다.
3) number[idx+1:]부터 다시 위의 작업을 반복한다.

def helper():
	nonlocal number, k, ans
        if len(number) == 1:
            number = str()
            k-=1
            return
        idx = 1
        max_val = int(number[0]) # 4, 7
        max_idx = 0 # 0, 2

        while idx <= k: # 1 <= 4
            if int(number[idx]) > max_val:
                max_val = int(number[idx])
                max_idx = idx
            idx += 1
        ans += number[max_idx]
        number = number[max_idx+1:]
        k -= max_idx

Solution 2

def sol2(number, k):
    
    stack = list(number[0])
    idx = 1
    
    while idx < len(number):
        if number[idx] > stack[-1]: # 증가한다면
            while stack and (stack[-1] < number[idx]) and k:
                stack.pop()
                k -= 1
        stack.append(number[idx])
        idx += 1
        if not k: break

    if k: return number[:-k] # 계속 감소하는 숫자일 경우 k가 남아있게 됨
    return ''.join(stack) + number[idx:]

결과 비교

Solution 1은 좋은 방법이 아니다. 항상 k+1개의 숫자들까지 max를 찾으러 loop을 돌고 비교하고 다음 helper()에서 또 다시 같은 작업을 반복한다면, 이전 helper()에서 loop을 돌았던 부분들을 다시 탐색하게 된다.
99988776, 7과 같이 max가 가장 앞에 있는 경우 k값이 줄지 못해서 최악의 경우엔 O(n^2)의 시간 복잡도를 가질 수 있다.

Solution 2는 O(n)으로 처리가 된다. 범위 내에서 가장 큰 숫자를 뽑고, 그 앞쪽 숫자들은 날려버린다는 개념은 비슷하지만 stack을 사용해서 중복되는 탐색을 없앨 수 있었다.

Solution 1로는 답을 구하는 데에는 지장이 없었는데, 아래와 같이 시간제한을 뚫을 수가 없었다. 중복되는 연산을 줄여갈 수 있도록 고민을 많이 해봐야겠다