프로그래머스 단어 변환
BFS, DFS를 세세한 부분까지 신경써가면서 구현해야 하는 문제였는데 재미있게 풀었던 것 같다. BFS가 최적의 경로로 답을 찾기 좋은 문제이지만, 개인적으로 구현은 DFS가 편하더라..
Question
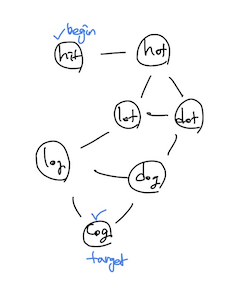
알파벳 한 글자만 바뀔 수 있고, words list의 단어들만으로 바꿀 수 있다는 조건 하에 begin 단어에서 target 단어로 바꿀 때 최소한의 작업의 수를 구하는 문제

Solution
나는 우선 그래프를 그렸다. words list 단어들 간에 변화 가능한 edge들을 표기했다. BFS, DFS 돌리기 편하려고.
def check(w1, w2):
ans = 0
for i in range(len(w1)):
if w1[i] != w2[i]: ans += 1
return ans == 1이런 식으로 한글자만 다른 관계의 단어들을 graph dict에 넣었다. (자세한 코드는 하단에 있는 github에서 볼 수 있음)
최단 거리는 BFS! 라고 편하게 생각하고 있었다. SNS에서 친구 간의 거리를 표현하듯.
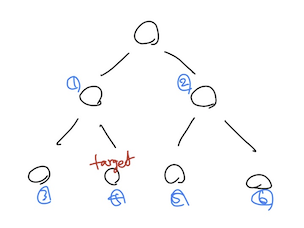
그런데 문제가 좀 있었다. 원래 하던 BFS 방식으로는 아래 그림처럼 정확한 거리를 뽑아내기가 어려웠다. 단순하게 탐색하는 순서대로 번호를 매길 경우 거리가 2인 target과의 거리가 4로 return 된다. 즉, level 단위로 거리를 체크할 수 있는 장치를 마련해야 하는 것이다. (평소 구현하던 BFS 방식과 좀 다른 부분이 있어서 시간이 꽤나 걸렸다)
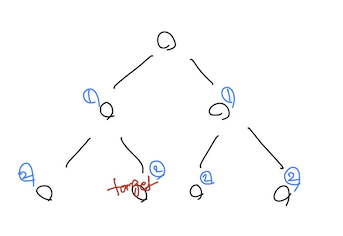
Easy DFS 반면 DFS는 자연스럽게 최단 거리가 나오게 된다. 곧장 leaf로 직진하기 때문이다. 다만 여기서도 한번 leaf에 도달하면 그 이전 단계에서는 path가 달라져야 한다. 그건 여기(link)에서 설명했듯이 재귀 함수를 호출하면서 list는 list[:]로, set은 set.copy() 등으로 고정된 값을 주면 해결된다.
속도 차원에서는 BFS가 빨라야 한다. DFS는 모든 도달 경로를 다 찾은 후에 최소 경로를 뽑는 것이고 BFS는 최소 경로에서 target이 발견되면 바로 return을 해버리기 때문이다. 코드의 중요한 부분은 아래에서 짧게 다루고 풀 코드는 하단 github에서 확인하면 된다.
Solution 1: level BFS
queue에 넣을 때, path level을 계산할 때 모두 level 단위로 list에 담은 후 넣었다. 그래야 나중에 length를 구할 수 있다.
queue = deque([[begin]])
level = list()
while queue:
cur = queue.popleft()
togo = list()
for w in cur:
togo += graph[w] # 다음 레벨의 todo들을 list에 모으고
togo = list(set(togo))
temp_level = [w for w in togo if w not in visited] # 실제 valid하게 갈 곳들만 남김
for loc in temp_level:
visited.add(loc) # 다음 level 갈 곳들을 visit 처리
queue.append(temp_level) # 마찬가지로 level 단위(list)로 처리
level.append(temp_level)
if target in temp_level: return len(level) # 다음 level 갈 곳에 target이 있으면 length 뱉어내면서 끝
Solution 2: DFS
DFS에서는 leaf에 갔다가 다시 돌아와서 또 다른 재귀함수를 호출할 때, path와 visited가 고정되어 있어야 한다는 점에 유의하자. path: List는 [:]로, visited: set는 .copy()로 복사하여 재귀 함수 호출 때 같은 레벨에서는 같은 값들이 들어갈 수 있도록 했다.
def dfs_helper(root, path, visited):
nonlocal graph, path_list, target
path.append(root)
if root == target:
return path_list.append(path)
visited.add(root)
togo = graph[root]
for loc in togo:
if loc not in visited:
dfs_helper(loc, path[:], visited.copy())