Data Driven Approach중 가장 단순하면서도 기초가 되는 분류법이 최근접이웃, Nearest Neighbor이다.
Nearest Neightbor
최근접이웃 (이하 NN) 기법을 설명하기전에 우선 컴퓨터가 이미지를 어떻게 인식하는지를 알아야한다.
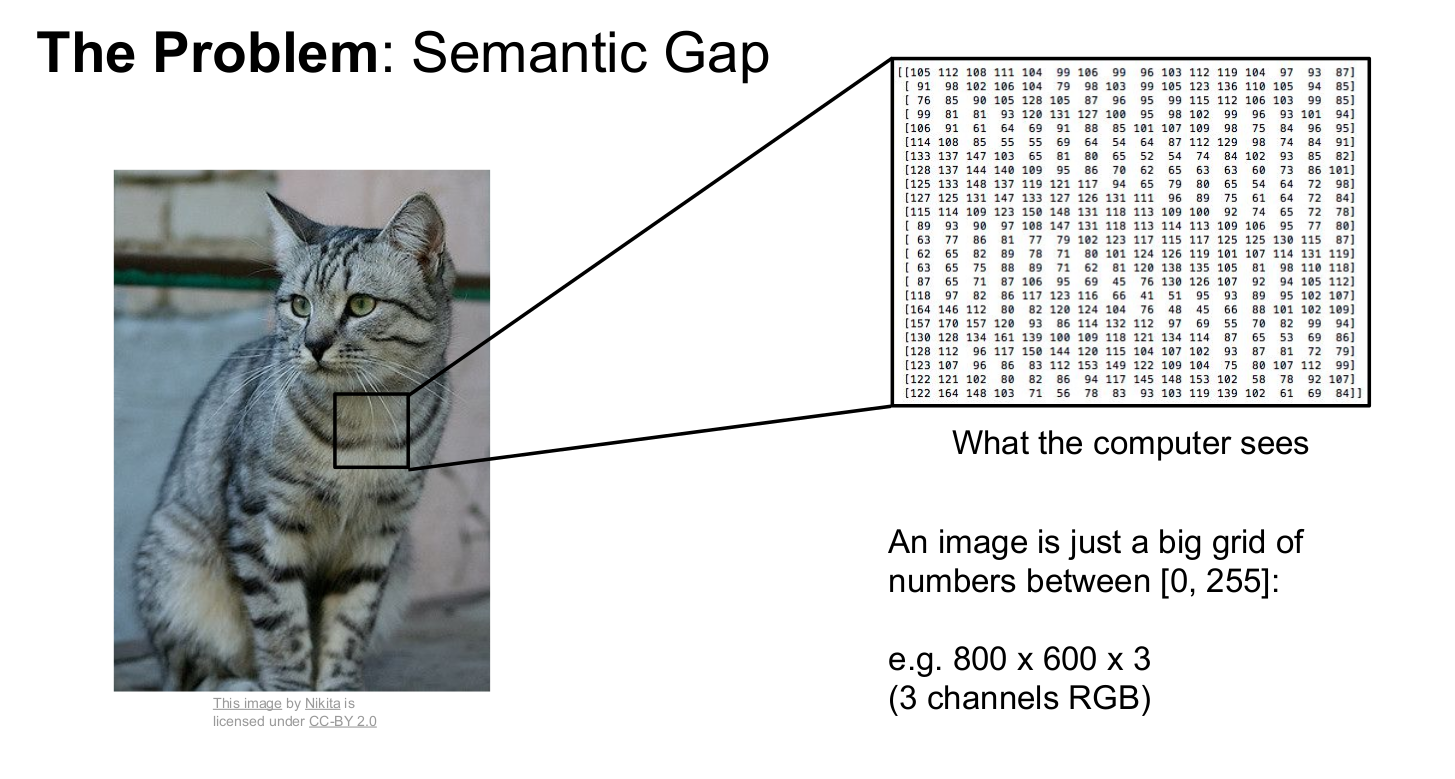
인간을 이미지를 보고 단순히 "고양이"라고 인식하지만, 컴퓨터는 픽셀에 심어져있는 숫자 정보를 인식한다. 이러한 인식방식의 차이를 semantic gap이라 한다.
컴퓨터는 이런식으로 이미지에대한 "숫자정보"를 인식하기때문에 수학적인 접근법을 이용한다.
L1 Distance (Manhattan Distance)

모델에게 제시한 테스트 이미지의 숫자 정보에서 학습한 이미지의 숫자 정보의 값을 뺀뒤 각 픽셀의 절대값을 모두 더한 수치로 분류하는 방법이다.
굉장히 단순하지만 성능이 떨어진다 (강사는 미련한 방법이라 칭했다;). 하지만 위 기법은 두 이미지를 비교할수 있는 기준을 제시해준다 라는 점에서 큰 의미를 갖는다.
L2 Distance (Euclidean Distance)
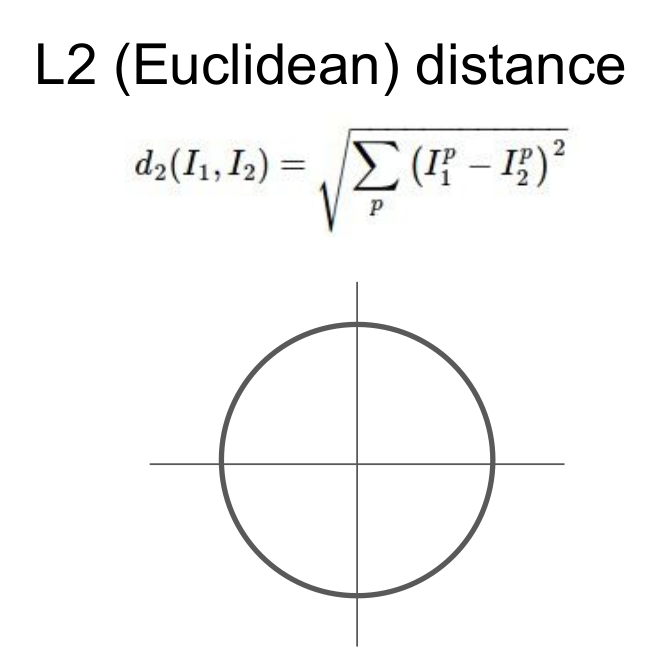
L2 Distance는 벡터사이의 차를 제곱한뒤 루트를 씌움으로써 두 벡터간의 직선 거리를 산출한다.
L1 vs L2
L1은 두 벡터 사이의 여러가지 경로값을 제공해주는 반면, L2는 가장 짧은 한가지의 직선 경로를 제공한다.
이해를 돕기위해 아래처럼 풀이를 그려봤다.
보는 바와 같이 L1 경로는 주황, 초록, 파랑 선분이고 L2는 빨간 선분이다.
L1은 두 벡터간 차의 절대값을 합함으로써 수직적인 선분이 나오지만,
L2는 제곱근의 루트를 이용함으로써 최단 직선으로 도출되며 피타고라스의 정리를 이용하여 값을 구할 수 있다.
L2가 최단거리를 제공한다해서 L1보다 효율적이진 않다. 모델에 맞는 보다 적합한 기법을 적용해주는게 이상적이다.
