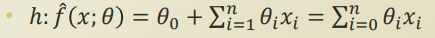
Linear Regression

머신러닝에서의 Function Approximation이란 확률적으로 가깝고 맞는 값을 가진 함수를 찾아나가는 과정이다.
여기서 선형 함수를 찾아나가는 과정을 Linear Regression이라 한다.

이를 위해 가설을 문자가 아닌 공식으로 표현한다.

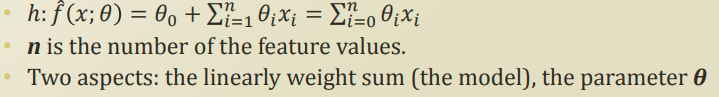
위의 함수를 풀어 설명하자면
x에대해 θ로 가중치를 둔 선형의 합을 통해 우리가 찾는 종속변수 (Dependent Variables)가 결정된다 라는 뜻이다.

이제 우리는 이 가설에 대해 두가지 관점을 가진다:
1) 이 가설은 선형(Linear)이다.
2) θ를 '잘' 정한다

위의 식에서 θ제로가 사라지는데 이는 절편값, 즉 상수값이기 때문에 의미가 없어 생략하는 것이다.
그럼 남는건 선형적 가중치 부분인데, x값은 이미 우리가 이 함수는 선형이다 라는 가설을 세웠기 때문에 건드리지 않고, θ의 값만 잘 찾아내면 적합한 함수를 구할수 있다는 뜻이다.

선형 회귀에서 θ를 찾아나가는 과정

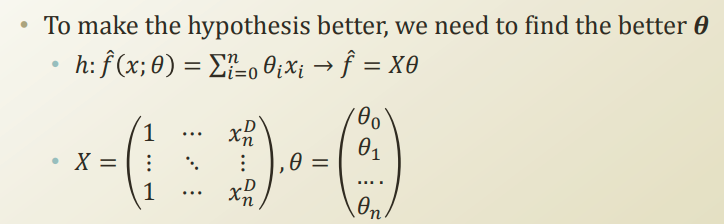
위에서 설명했듯이 세타제로를 드랍해버리면 가설은 f^(hat) = Xθ과 같은 간단한 형태를 띈다.
그리고 X와 θ는 우리가 찾고자 하는 값에 영향을 주는 독립변수만큼의 갯수를 지니기 때문에 행렬로 표시된다.
f에 hat을 씌우는 이유는 현실에서 나타날수있는 에러가 제외되었기때문에 씌어진 것이다.
우리가 궁극적으로 원하는것은 이 에러값이 최소가 되는 θ값을 찾음으로써, 최적의 선형 회귀 모델을 구현하는게 목표인 것이다.

최적의 θ값을 구하는 공식은 아래와 같다.

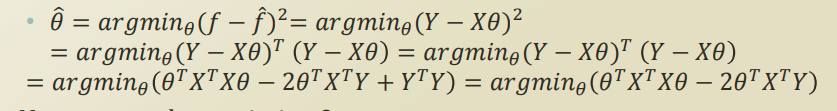
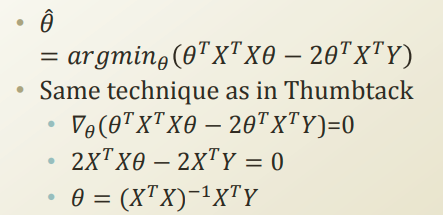
미분을 통한 극점을 찾는 방법으로 위의 공식이 유도되며 이로 찾은 세타, X, Y값을 그래프로 그려보면 아래와 같이 나온다.

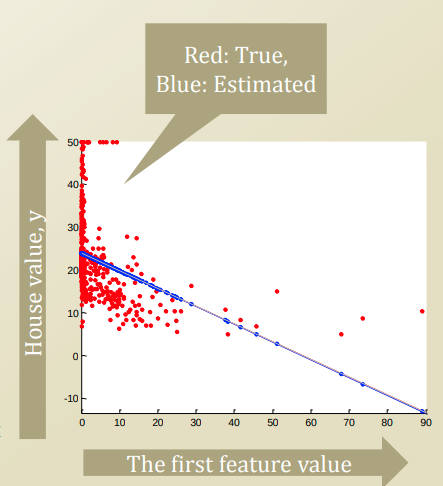
빨간 점은 실제 데이터이고,
파란 선분은 추정치로, 실제 데이터를 가장 잘 나타내는 선분 (최적의 θ)를 뜻하며, 새로운 데이터가 생기게 되어도 이 선형 공식을 통해 Y값을 예측할 수 있다.