전처리
독립변수가 열이 나뉘어져 있다면 전처리 작업을 해야함
예제1
ind = c( rep("A반", 30),rep("B반", 30),rep("C반", 30))
dep = c( dt[,2],dt[,3],dt[,4])
dt_f = data.frame(ind, dep)
### boxplot
boxplot(dep~ind, dt_F)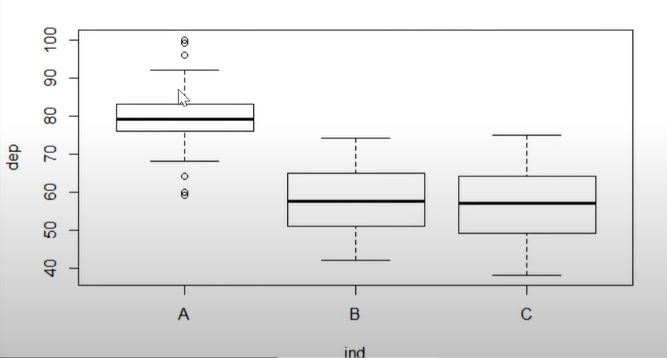
예제2
이미 독립변수 열이 합쳐져 있음
dt = as.data.frame(Telco)
dt$PaymentMethod <- ordered(dt$PaymentMethod) ## 범주화 하기
dt <- na.omit(dt) ## 결측치 제거독립성 확인
예제 1
각 반이 독립되어 있으므로 독립
예제 2
각 결제 방식에 따라 나뉘어 있으므로 독립
정규성 확인
예제1
각 반이 30명 이상이 되기 때문에
정규성이 된다고 봄
예제2
table(dt$PaymentMethod)
Bank transfer (automatic) Credit card (automatic) Electronic check
1542 1521 2365
Mailed check
1604 각 표본이 1000개가 넘으므로 정규성이 있다고 봄
등분산 확인
levene test
레벤 테스트(Levene's Test)는 통계학에서 분산의 동질성을 검정하는 방법입니다. 동질성이란 두 개 이상의 모집단에서 추출된 표본들이 공통적으로 가지는 분산(변동성)이 같음을 의미합니다.
레벤 테스트는 특히 분산 분석(ANOVA)과 같은 통계적 분석을 수행하기 전에, 해당 분석의 전제 조건 중 하나인 분산의 동질성을 만족하는지 검정하기 위해 사용됩니다.
레벤 테스트의 귀무 가설은 "모든 표본 그룹들의 분산이 동일하다"이며, 대립 가설은 "적어도 하나의 그룹의 분산이 다른 그룹과 다르다"입니다.
테스트 결과 p-value가 특정 유의 수준(예: 0.05)보다 낮으면, 귀무 가설을 기각하고 분산이 동질하지 않음을 결론지을 수 있습니다.
예제 1
library(lawstat) ##levene.test
levene.test(dt_f$dep, dt_f$ind, location ='mean')
> p-value = 0.8149 -> 등분산성이 보장된다.예제 2
levene.test(dt$TotalCharges, dt$PaymentMethod, location ='mean')
> data: dt$TotalCharges
Test Statistic = 295.05, p-value < 2.2e-16
등분산성이 보장되지 않는다CHAT GPT said
Levene 검정에서 p-value가 매우 작은 값을 갖는다면, 그것은 귀무가설(모든 그룹의 분산이 동일하다)을 기각한다는 것을 의미합니다. 즉, 그룹 간의 분산이 동일하지 않다는 것을 나타냅니다. 이는 등분산성 가정이 충족되지 않았음을 나타냅니다.
그러나 이것이 반드시 ANOVA 분석을 할 수 없다는 것을 의미하지는 않습니다. 분산이 동일하지 않은 경우에도 ANOVA를 사용할 수 있지만, 이 경우에는 조금더 견고한 버전의 ANOVA를 사용해야 합니다. 이를 위해 Welch's ANOVA 또는 Brown-Forsythe test 등을 사용할 수 있습니다.
또는, 데이터를 변환하여 분산을 동일하게 만드는 방법도 있습니다. 로그 변환, 제곱근 변환 등이 이에 해당합니다.
따라서, Levene 검정에서 등분산성이 충족되지 않더라도 다른 방법을 통해 분석을 계속 진행할 수 있습니다.
분산분석
예제 1
aov 패키지 이용
aov(formula , data = , projuections = , qr ...)
result = aov(dep~ind,dt_F)
summary(result) ## 위의 aov 분석에는 p-value 가 안나와서 하는 것
p-value = 4.62e-15 p-value 가 0.05 보다 작아서 귀무가설이 기각된다.(유의미하다=사후검정 필요)
예제 2
기본적인 aov 와
등분산성이 없을 때 사용하는 Welch's ANOVA - oneway.test()를 이용
result = aov(dt$TotalCharges~dt$PaymentMethod, dt)
summary(result)
Df Sum Sq Mean Sq F value Pr(>F)
dt$PaymentMethod 3 4.431e+09 1.477e+09 327.5 <2e-16 ***
Residuals 7028 3.170e+10 4.510e+06
result <- oneway.test(TotalCharges ~ PaymentMethod, data = dt)
print(result)
data: TotalCharges and PaymentMethod
F = 437.07, num df = 3.0, denom df = 3637.2, p-value < 2.2e-16결과는 둘다 p-value 가 0.05 보다 작아서 귀무가설이 기각된다.(유의미하다=사후검정 필요)
정규분포를 따르는 경우 사후검정의 분류
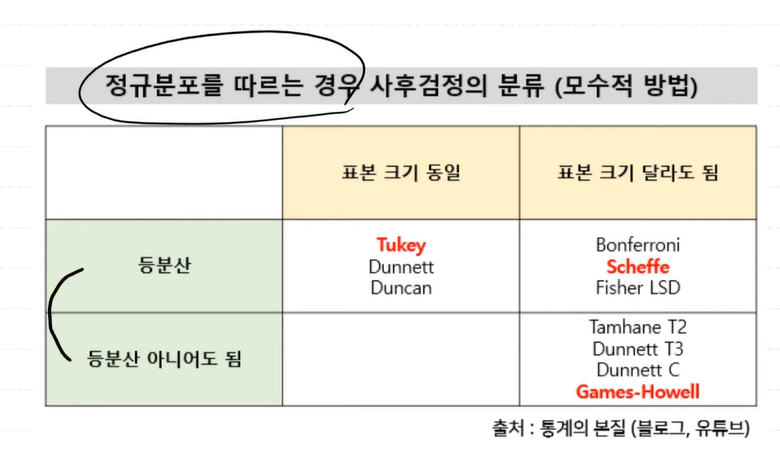
예제 1(tukey 투키 검정)
등분산 + 표본크기 동일
TukeyHSD(x)
x=aov result
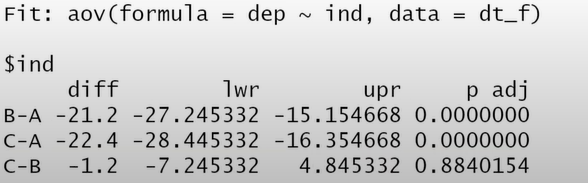
A반과 B반, A반과 C반의 유의미한 차이가 존재 -> 이것이 귀무가설이 기각된 이유
B반과 C반은 차이가 없다.
예제 2(games-howell 검정)
# 패키지 로드
library(PMCMRplus)
# Games-Howell 검정 실행
result <- gamesHowellTest(TotalCharges ~ PaymentMethod, data = dt)
print(result)
Bank transfer (automatic) Credit card (automatic) Electronic check
Credit card (automatic) 1 - -
Electronic check < 2e-16 < 2e-16 -
Mailed check < 2e-16 < 2e-16 2.3e-08
P value adjustment method: none
alternative hypothesis: two.sidedEstimated marginal means 를 보기 위해 패키지를 찾아봤다
# 패키지 로드
library(emmeans)
library(ggplot2)
# emmeans 계산
emmeans_results <- emmeans(result1, "PaymentMethod")
# emmeans 결과를 데이터프레임으로 변환
emmeans_df <- as.data.frame(emmeans_results)
# ggplot2를 사용하여 그래프 출력
ggplot(emmeans_df, aes(x=PaymentMethod, y=emmean)) +
geom_point() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL), width = 0.2) +
theme_minimal() +
labs(x = "Payment Method", y = "Estimated Marginal Mean", title = "EMM Plot")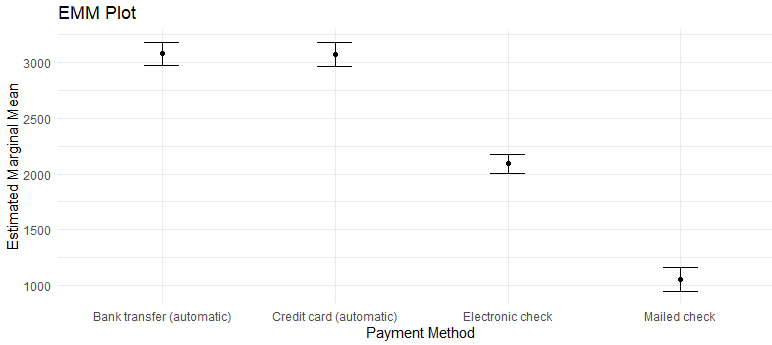
결과
credit car - bank transfer는 차이가 없다.
Electronic check - Bank transfer , -Credit card 는 차이가 있다.
Mailed check - Bank transfer, - Credit card, - Electronic check 는 차이가 있다.
