[통계] t-test (3) 실전

양측검정과 단측검정의 선택은 연구자/조사자의 선택
단순히 두 집단이 다를 것이다라고 까지만 생각되면 양측검정,
두 집단이 다른 것 뿐만아니라 한쪽이 더 크거나 작을 것이다라고 (기존 연구나 학습을 통해)확신하면 단측검정을 사용

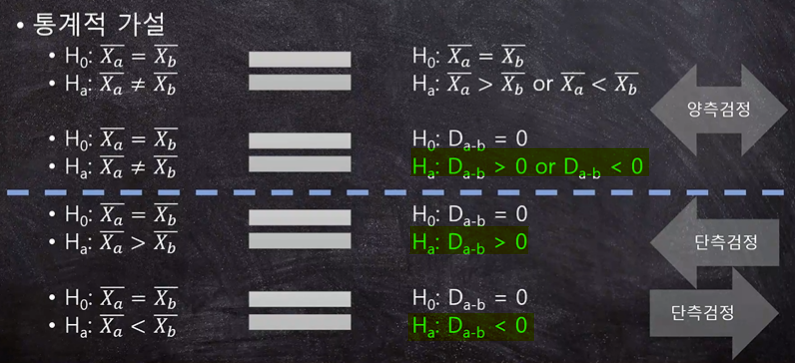
양측검정

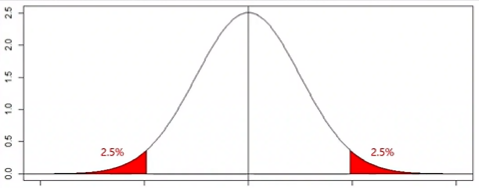
단측검정

진짜 t-test를 해보자

1. A대학과 B대학의 키 차이는,
   어디가 더 큰지 알 수는 없으므로 양측검정을 사용한다.

2. Q : t-test의 목적이 뭐였지?
   A : 두 집단의 평균값 같은지 다른지 알고 싶다

3. 두 집단간 비교를 위해
   z-test에서는 z-값과 표준정규분포를 이용했다.
   t-test에서는 t-값과 t-분포가 필요하다.

**제일 이해 안되는 부분 : sqrt(n)의 역할은 무엇인가?
두 집단의 평균값의 difference(차이)가 표준편차만도 못하다면, 두 집단의 차이는 우연히 발생했다고 본다.

우리가 데이터를 더 모을수록(=df 자유도가 높아질수록) 표준정규분포와 근사해짐
표본의 크기(n)이 커지면 커질수록 t-값은 커지고(분모의 분모가 커지면 분모가 작아져서 값이 커짐)
표본의 크기(n)이 커지면 커질수록 t-분포는 표준정규분포에 근사

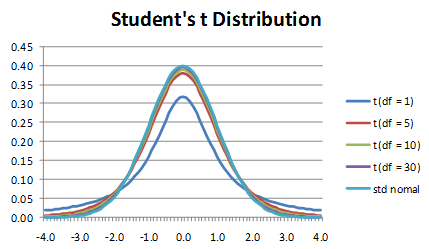
t-test에서 자유도(df)는 n-1로 계산되므로, 표본의 크기가 커지면 자유도가 커지고, 자유도가 커졌다는 의미는 우리가 t-분포에 묶여있다가 자유롭게 표준정규분포를 사용할 수 있음을 의미

4. 만약 표준편차(s)가 7.05cm 였고, 표본의 크기가(n) 101명이라면
   -> t-value = 1.4/(7.05/sqrt(101)) = 1.996
   t-table critical value = 1.984 (표 참조)
   

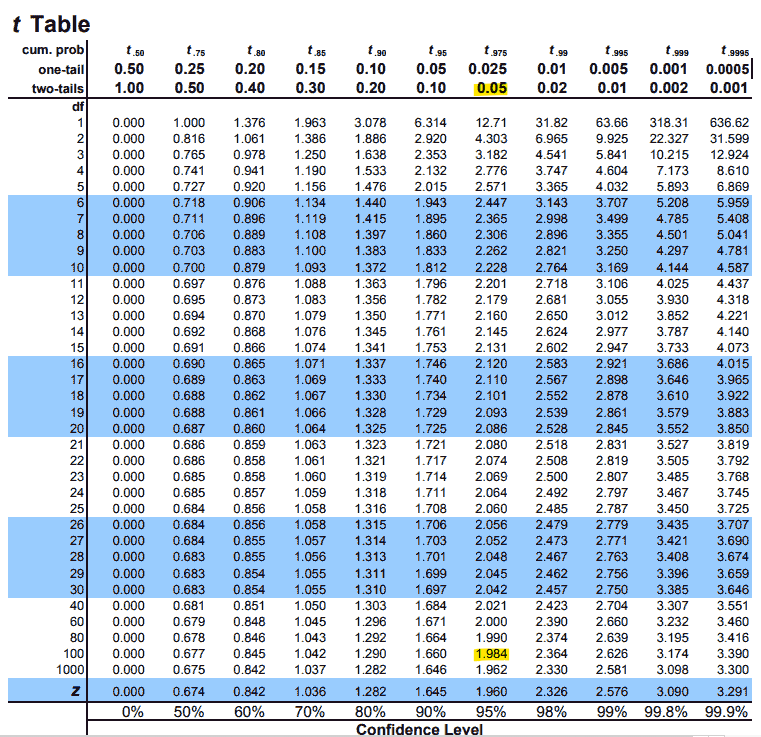
t-value > critical value보다 크므로 5% 이내에 들 것으로 보임
이 차이는 통계적으로 유의하다.

그러므로, 두대학의 학생의 키는 통계적으로 유의하게 다르다.

이 뜻은 두 대학 학생의 평균키 차이인 1.4cm가 우연히 발생했을 확률은 5%보다 작으며,
이는 우연히 발생했다고 보기 어려워(현재로서는 정확한 이유는 모름) 두 대학의 학생의 키가 다른
뭔가 다른 원인이 있다고 볼 수 있다.
-> 이후 다른 테스트를 통해 원인을 찾아봄

• 학습 링크
  https://www.youtube.com/watch?v=EzH5n31Com0&list=PLalb9l0_6WArHh18Plrn8uIGBUKalqsf-&index=5