t-test를 이해하기 위해선 정규분포를 이해해야 한다.
대부분의 경우 정규분포의 z-test 와 t-test를 단순/별도로 설명하지만 연결해서 볼 필요가 있다.
본질적으로는 같기 때문!
모집단 <- z-test
표본(샘플) <- t-test
우리는 모집단을 가지고 테스트를 할 수가 없다.(거의 없다본다. 인구 전체를 어떻게함..?)
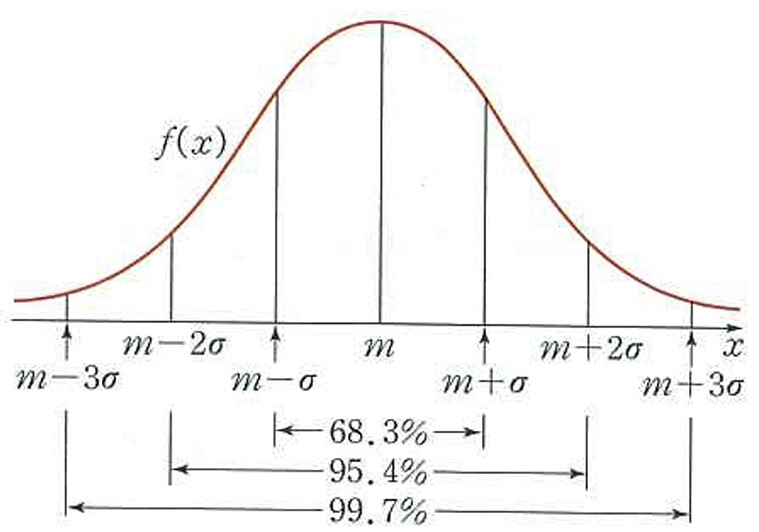
정규분포의 특징
- 종모양, 평균을 중심으로 좌우 대칭
- 양 끝은 영원히 0에 닿지 않음
- 평균과 표준편차만으로 규정됨
- 면적은 확률을 의미함. (모든 면적의 합은 1)
- 따라서 정규분포를 이용한 확률을 구하려면 적분을 해야함.
표준정규분포는 왜 존재 하는가?
무한 개수의 정규분포 곡선을 적분하는 번거로움을 덜기 위해.
표준정규분포 = 평균(μ)이 "0"이고, 표준편차(σ)가 "1"인 정규분포
어떻게 이용할까?
예시
- 신입생 1000명을 대상으로 영어시험을 시행
- 영어점수의 분포가 정규분포에 근사
- 평균점수는 82이고 표준편차는 5
Q. 이때 82점부터 90점까지의 점수를 받은 학생 수는?
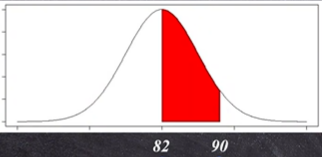
위 면적을 적분한다 ? ??
불가!
-> 1. 정규분포를 표준정규분포로 바꾼다. Z(82) z-score = 0 / Z(90) z-score = 1.6
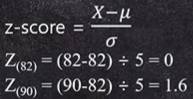
-
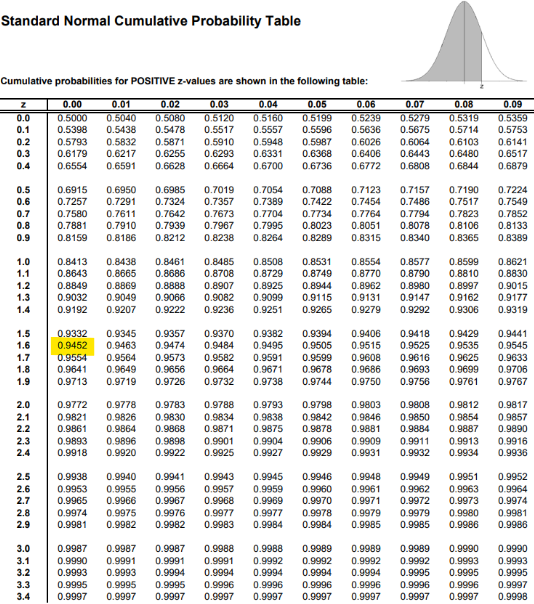
'표준정규분포표'라는 확률표를 만들어뒀음 z-score = 1.6 > 0.9452
-
0 <= z-score <= 1.6 사이의 값이므로 0.9452 - 0.5 = 0.4452
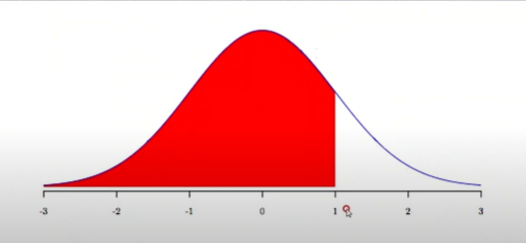
-
0.4452 * 1000 = 약 445명
z-score를 가지고 하는 테스트를 z-test라고 함
z-test는 z값과 표준정규분포표를 이용해서 진행
z-score(z값)으로 변환하는 것을 z-transformation or standardization(표준화)라고 함.
z값은 단위로부터 자유롭다.
z-score = (X - μ) / σ
1 표준편차당 관찰값(X)가 평균으로부터 얼마나 떨어져있는가를 의미
이걸 가지고 어쩌라고?
정규분포곡선의 아래 면적이 확률
-> 어떤 사건이 우연히 발생할 확률이 얼마일까?
-> 여기서 말하는 확률이 정규분포곡선 아래 면적인 그 확률과 같다.
다만 t-test를 할 때는 정규분포를 쓰지 않고 다른 분포 곡선을 사용.
