회귀분석의 표준화계수

표준화계수란?

종속변수에 대한 독립변수들의 단위(scaling)을 통일시긴 계수
모든 독립변수를 같은 단위로 상정하고 비교 가능

특징

원점(0,0)을 지나가 절편이 "0"임
해석이 어렵다

장점

여러 독립변수의 상대적 중요도를 비교 가능

주의사항

표준화 계수의 크기는 별도의 테스트를 해서 크다/작다를 말할 수 있음

2. 더미변수

더미변수란 ?

값이 오직 0 과 1로만 이루어진 변수
수리적 의미 없음, 기본적으로 이산형/범주형 변수인데 이를 연속형 변수처럼 사용

왜 더미변수를 사용할까?

범주형 변수의 경우 그 범주의 개수가 3개 이상일 경우
코딩을 1, 2, 3 이런식으로 하면 연속형 변수가 되어 회귀분석에서 사용 못함

더미변수 만들기 예제

변수의 범주 : 4개의 범주
필요한 변수의 개수 : 범주의 개수 - 1 = 3

더미변수 해석

빠진 범주가 비교의 기준(reference group)이 됨

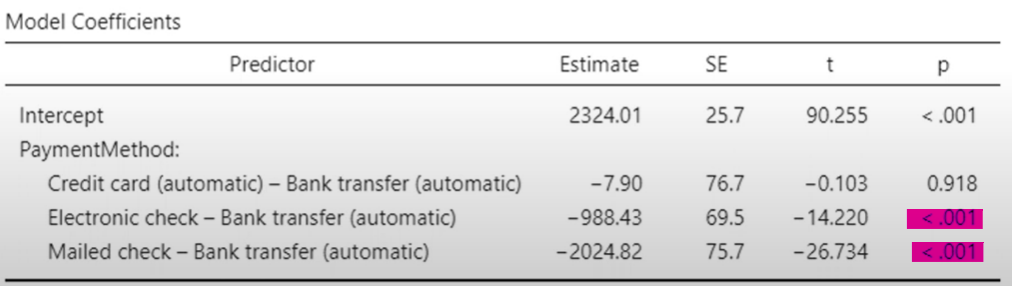
1. credit 과 bank 의 차이는 무의미하다.
2. electroci check 가 bank transfer 보다 988만큼 덜 지불 하더라
3. mailed check 가 bank transfer 보다 2024만큼 덜 지불 하더라

그런데, 만약 Electronic check과 mailed check을 비교하고 싶다면?
현재의 결과표로는 해석 불가.
비교하고 싶은 범주중 한개를 reference group로 하는 더미변수 3개를 다시 만들어야함

결론

더미변수는 값이 오직 0, 1
수리적의미 없음

해석할 때는 해당 범주와 기준 그룹 간에 유의한 차이가 있다/없다로 해석
기준 그룹이 아닌 범주와는 해석 불가

다중공선성

결론

유사한 독립변수들이 동시에 모델에 들어감으로써 발생하는 문제
완벽한 다중공선성이 있으면 최소제곱법 계산이 되지 않음
다중공선성이 높을 경우 회귀계수의 표준오차가 비정상적으로 커짐

• 유의해야할 변수가 유의하지 않아질 수 있음
  일반적으로 VIF 10을 기준으로 하나 더미변수는 3으로 보아야함
  

해결책

높은 다중공선성에도 불구하고 유의하다면 그대로 좋음
유의해야할 변수가 유의하지 않다면 변수 중 뭔가를 빼야 함
다른 여러 방법이 있으나 일반적으로 완벽하지 않음
강제로 분산을 제거하는 방법이 더 큰 문제를 만들 수 있음

이분산성(Heteroskedasticity)

결론

회귀계수의 표준오차가 동일하지 않고 변화하는 경우
회귀계수의 표준오차가 독립변수의 함수로 나타남

확인 방법

• 산포도
• 잔차도
• White test

해결 방법

• robust standard error
• WLS regression(이론적으로는 쉬우나 현실적으로 어려움)