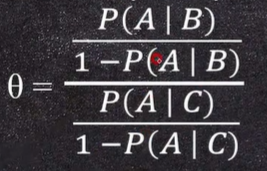
1. 회귀분석이란?
- 회귀(Regression)이란 말은 어딘가로 돌아간다는 의미
- 어디로 돌아가는걸까?
회귀분석의 목적
- 주어진 독립변수로 종속변수를 예측하기 위해
- 단순 회귀(Simple regression)
- 독립변수 1개 / 종속변수 1개
- 다중 회귀(Multiple regression)
- 독립변수 2개 이상 / 종속변수 1개
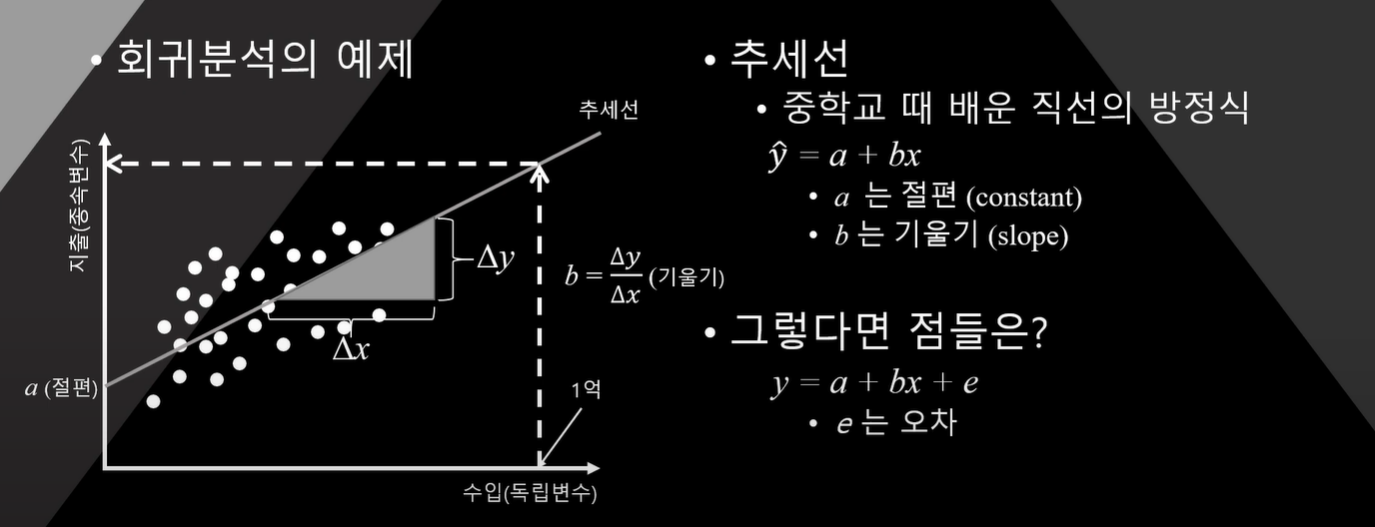
- 만약 수입이 1억이라면? 지출은 얼마일까?
이를 예측하기 위해 필요한 건 추세선
이 추세선을 구하는 방법이 회귀분석
회귀분석의 오차가 발생(error)
오차 = 측정값 - 예측값
그렇다면 가장 합리적인 추세선이란?
오차가 가장 작은 추세선?
그런데 오차에 + - 가 혼재.. 어떻게할까?
오차의 제곱이 최소화된 추세선
-> 오차의 제곱합이 최소화된 추세선
어디서 본거 같은데...........?
방법 중 하나 [최소제곱법]
앞의 a와 b를 추정하는 방법
궁극적으로는 평균을 지나는 추세선이 가장 합리적인 최소제곱법에 의해 구해짐
결론
주어진 데이터의 독립변수로 종속변수를 예측
이를 위해 직선형태의 추세선을 구함
이 추세선의 식은 y = a + bx (a 는 절편, b는 기울기)
사용되는 방법은 최소제곱법(오차의 제곱의 합을 최소로 만듬)
최소제곱법으로 구해진 직선이 우리가 원하는 회귀분석식
- 이 직선은 평균을 지난다(평균으로의 회귀)
- 이 방법을 영어로 Ordinary Least Square(OLS)라고 함
2. 회귀분석의 결과표 해석

intercept = 상수
SE(비표준화계수/ Standard error 표준오차)
Estimate(비표준화계수/ B, 회귀계수)
연구가설
거실의 크기가 클수록 매매가격이 비쌀 것이다.
결과해석
거실크기가 1 feet^2 증가할 때, 매매가격은 281$ 증가
3. 회귀분석과 표준오차
통계적인 사고 방식 Remind!
- 이 사건이 우연히 발생하지 않았을까?
- x가 1증가할 때, y가 2.4증가하는게 우연이 아니었을까?
최소제곱법은 오차의 제곱합이 최소가 되는 회귀방정식을 구해줄 뿐 이 회귀식의 회귀계수가 우연인지 아닌지 알려주지 않는다.
그렇다면 우리는 회귀계수 2.4가 우연인지 아닌지 어떻게 판단해야할까
비교 대상이 필요하다
표준오차(SE)
우리는 뭘 하든지 대부분 모집단이 아닌 표본으로 통계분석 함.
우리가 가진 표본이 얼마나 모집단에 가까운지 아닌지 판단해야 함.
모집단의 평균을 평균의 참값이라고 할 때,
- 표본집단의 평균이 얼마나 모집단의 평균과 가까운지 먼지를 계산
- 이론적으로 같은 모집단에서 적합한 방법으로 표본을 구해도 표본집단의 평균은 매번 다를 수 밖에 없음
표준오차 = 표본 평균들의 표준편차
결론적으로 표준오차가 작으면 참값에 더 가깝다는 것이고, 표준오차가 크면 참값에서 더 멀다는 것임
결론
회귀계수는 최소제곱법으로 구해진다.
그러나! 그렇게 계산된 회귀계수가 우연인지 아닌지는 모른다.
그래서 이 회귀계수가 우연일 확률을 알기 위해 표준오차를 사용한다.
표준오차가 작으면 회귀계수가 우연일 확률이 낮다
- 표준오차가 작다 = 데이터가 회귀직선 가까이에 퍼져있다.
표준오차가 크면 회귀계수가 우연일 확률이 크다 - 표준오차가 크다 = 데이터가 회귀직선에서 멀리 퍼져있다
그렇다면 이 확률을 어떻게 계산할까?
-> t-test
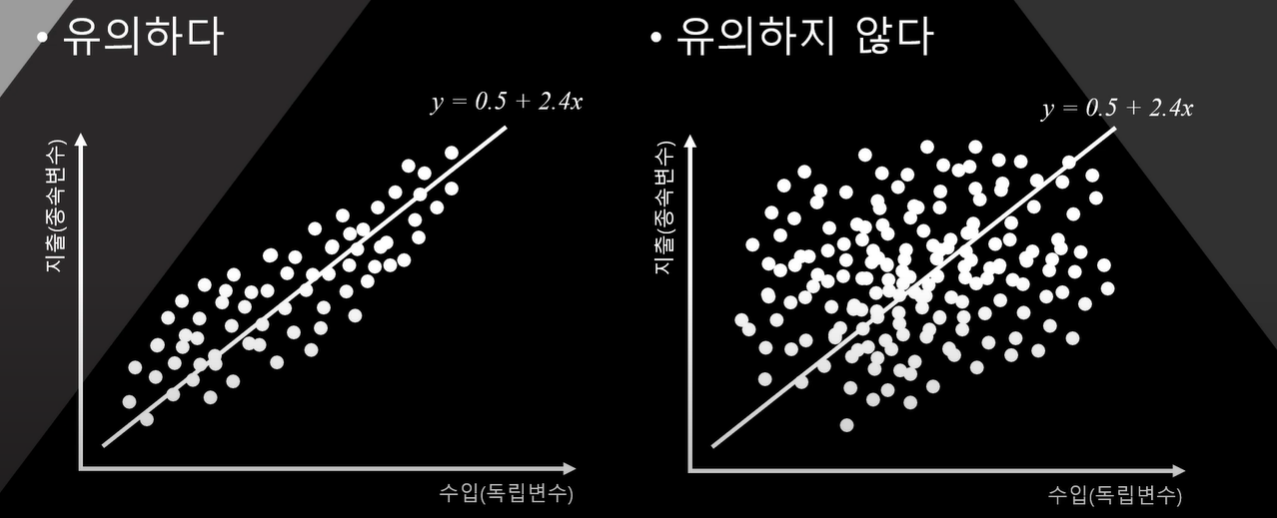
4. 회귀분석과 t-test
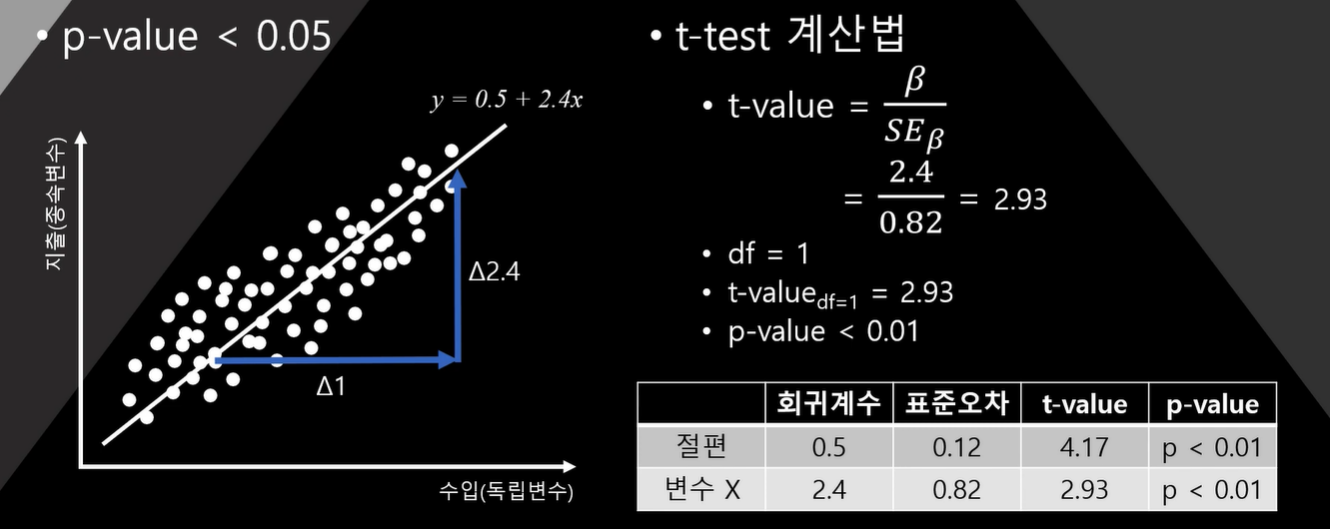
- 유의미한 회귀계수 2.4가 됨
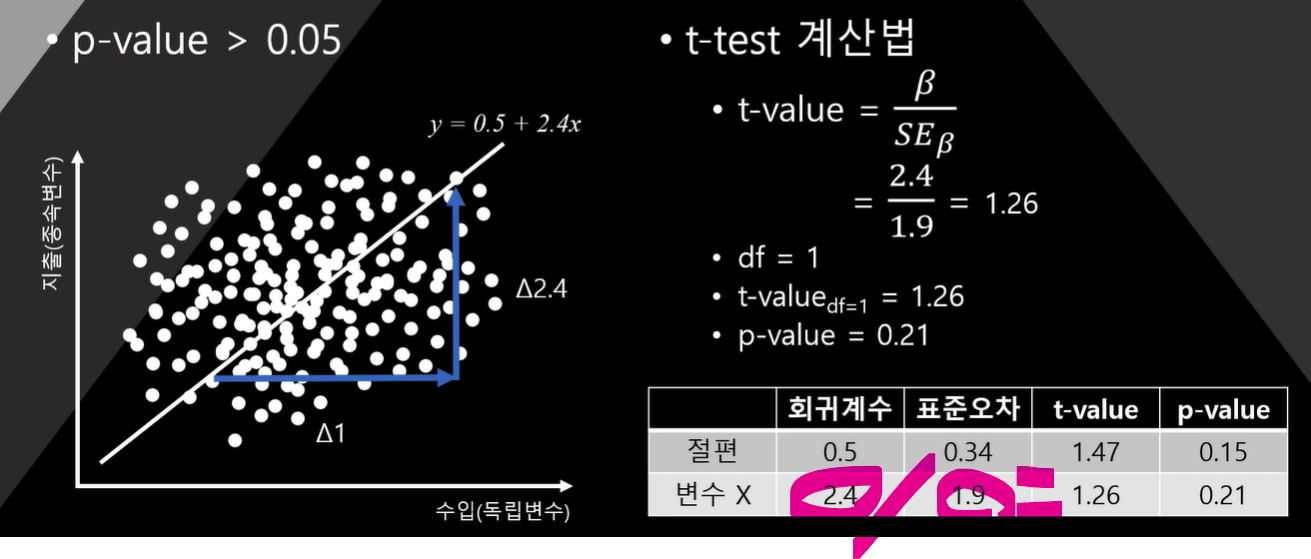
- 우연히 나온 회귀계수 2.4가 됨
회귀분석의 특징
데이터가 곡선 형태로 되어 있다면 기울기는 0
원 형태로 되어 있다면 기울기는 0
직선의 형태로 되어 있지 않다면 분석할 수 없음
- 회귀분석 전에 산포도를 찍어 보아야 함.
- 직선 형태의 데이터분포가 나타나지 않으면 다른 방법 찾아야함
- 회귀분석은 y = a + bx니까!
- 회귀계수(기울기)는 결국 t-test의 평균값 차이와 동일한 개념
- 따라서 회귀계수는 t-test로 그 유의성을 테스트 함.
회귀계수 t-test의 통계적 가설
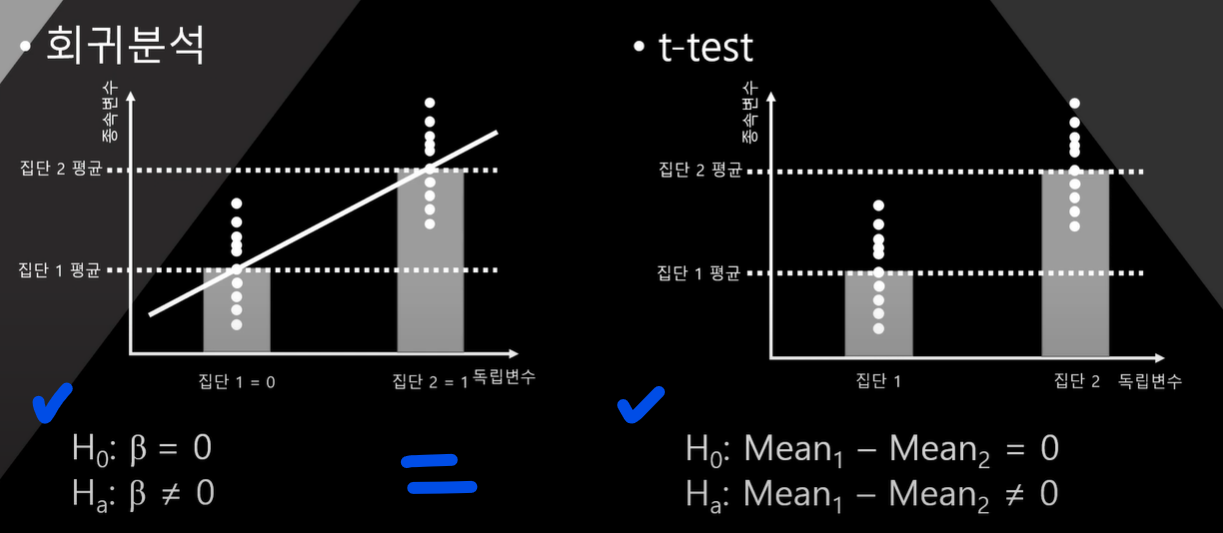
결론
- 회귀분석은 독립변수와 종속변수의 직선관계만 분석가능
이를 위해 분석 전에 산포도 확인 - 직선관계가 아닌 경우 잘못된 회귀계수를 얻게 됨.
- 회귀분석 기울기의 테스트는 t-test와 동일한 개념
회귀계수를 표준오차로 나누면 회귀계수
이때 자유도는 1
독립변수가 증가할 수록 자유도가 증가
-
무한대의 독립변수를 사용 못함
-
독립변수 1개의 추가는 곧 비용임(자유도 늘어나니까!)
R² 를 어떻게 해석해야할까
-
보통 회귀분석에서는
종속변수와 독립변수의 인과관계를 논리적/이론적으로 전제하고
독립변수로 종속변수를 설명하려 한다. -
그런데 회귀분석 뿐만 아니라 우리가 하는 통계는 결국
분산을 얼마나 잘 설명하는가 가 목적이다.
즉, 회귀분석이란 종속변수의 분산을 독립변수로 얼마나 설명할 수 있는가의 과정
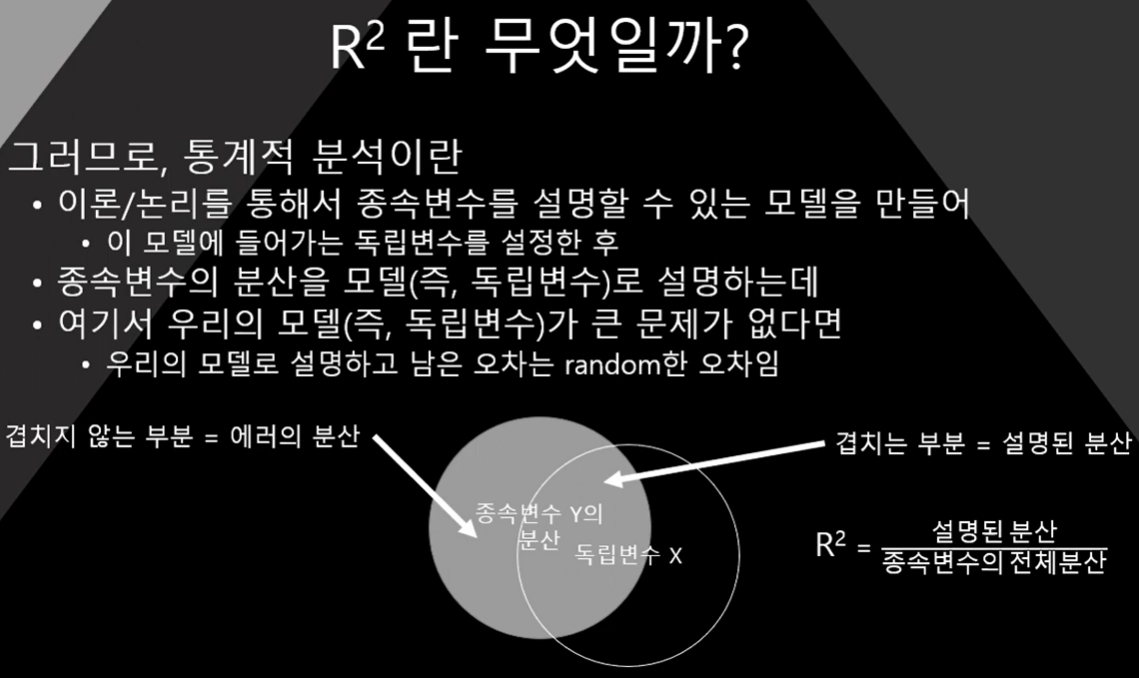
R² = 모델의 분산 설명력
모델(독립변수)가 얼마나 데이터를 잘 설명했는지를 의미
R²가 높으면 무조건 좋은 것인가?
절대 그렇지 않음
나름 의미는 있으나 높은 R2가 모든 것을 완벽하게 하지는 못함
- 잔차도가 랜덤하게 분포함을 확인해야함
- 의미 없는 독립변수의 추가 조차도 R²를 약간이라도 증가시킴
- 그러나 독립변수의 추가는 자유도를 1 증가시켜 비용이 발생
- 높은 R² 는 과적합 문제로부터 자유롭지 않음
잔차도(residual plot)
종속변수의 분산을 모델(독립변수)로 설명하는데
여기서 모델이 큰 문제가 없다면, 모델로 설명하고 남은 오차는 random한 오차임
랜덤하지 않은 분포는 R²가 아무리 높더라도 모델 설명이 안됨.
뭔가 다른 이유가 있기 때문이라고 판단할 수 있음
R² 대신 사용할 수 있는 것은?
R²의 단점은
독립변수가 무한대로 증가하면 (변수가 무관하더라도) R²가 증가함
따라서 독립변수의 증가 = 자유도 1 손실
이에 대한 보정이 필요
- 보정 ?
- 추가된 독립변수가 자유도 1을 잃고도 충분히 분산을 설명했는지 여부
- 자유도가 감안된 R²가 필요
- 이것이 adj. R²(수정 R²)
- 둘의 크기가 심하게 다르다면 의미 없는 독립변수를 너무 많이 넣었다는 의미
과적합(overfitting , overestimation)
- 여전히 주의할 것은 우리는 거의 표본만을 대상으로 분석한다는 사실
- 만약 모델이 이번에 수집한 표본에서만 높은 R²을 보인다면?
- 이것은 단한번 우연히 이 표본에만 적합할 뿐
- 다른 표본에서는 절대 높은 R²을 확인할 수 없다는 것을 의미
- 이 표본에서만 우수함
- 따라서 이 모델은 큰의미 없음
과적합 판단 및 해결책
- Cross-validation 을 적용
표본을 랜덤하게 둘로 나누어 한 표본에서 모델을 구축하고 난 뒤
다른 표본에서 모델의 적합성을 다시 테스트함
결론
R²는 애증의 대상..
- R²는 모델이 데이터를 얼마나 잘 설명했는지 의미
- R²가 높다는 건 모델의 설명력이 높으므로 나름 좋은 의미
- 그러나, 높은 R²가 모델의 정당성을 모두 해결해주지 않음
R²의 단점
- R²를 높이는 것이 단일 목적인 경우 무한히 많은 독립변수를 추가
- 그러나 독립변수의 추가는 결국 비용이고 손해임(장ㅍ도 1손실)
- 그러므로 adj. R²를 사용 하는 것이 좋음
R²보다 중요한 것
- 모델에 사용된 독립변수의 논리성/이론적 근거
