2차원 누적합

2차원 누적합

2차원 누적합은 2차원 배열의 누적합을 구할 때 사용한다.

N * M 배열에서 N이 최대 1만, M이 최대 1만, 질문의 수가 10만이라고 할 때

2차원 구간의 합을 직접 for문으로 구하는 경우

일반적으로 구간합을 구하려면 시간 복잡도는 O(NM + QNM) = O(QNM) 이므로 10^13이 된다.

1차원 누적합을 행마다 계산하는 경우
누적합 알고리즘을 사용하여 한 줄씩 구현할 수 있지만 시간 복잡도는 O(QN)이 돼 10^9로 1초 이내 통과할 수 없다.

그러므로 2차원 배열의 누적합을 구해야 하는 경우 2차원 누적합 알고리즘을 사용해야한다.

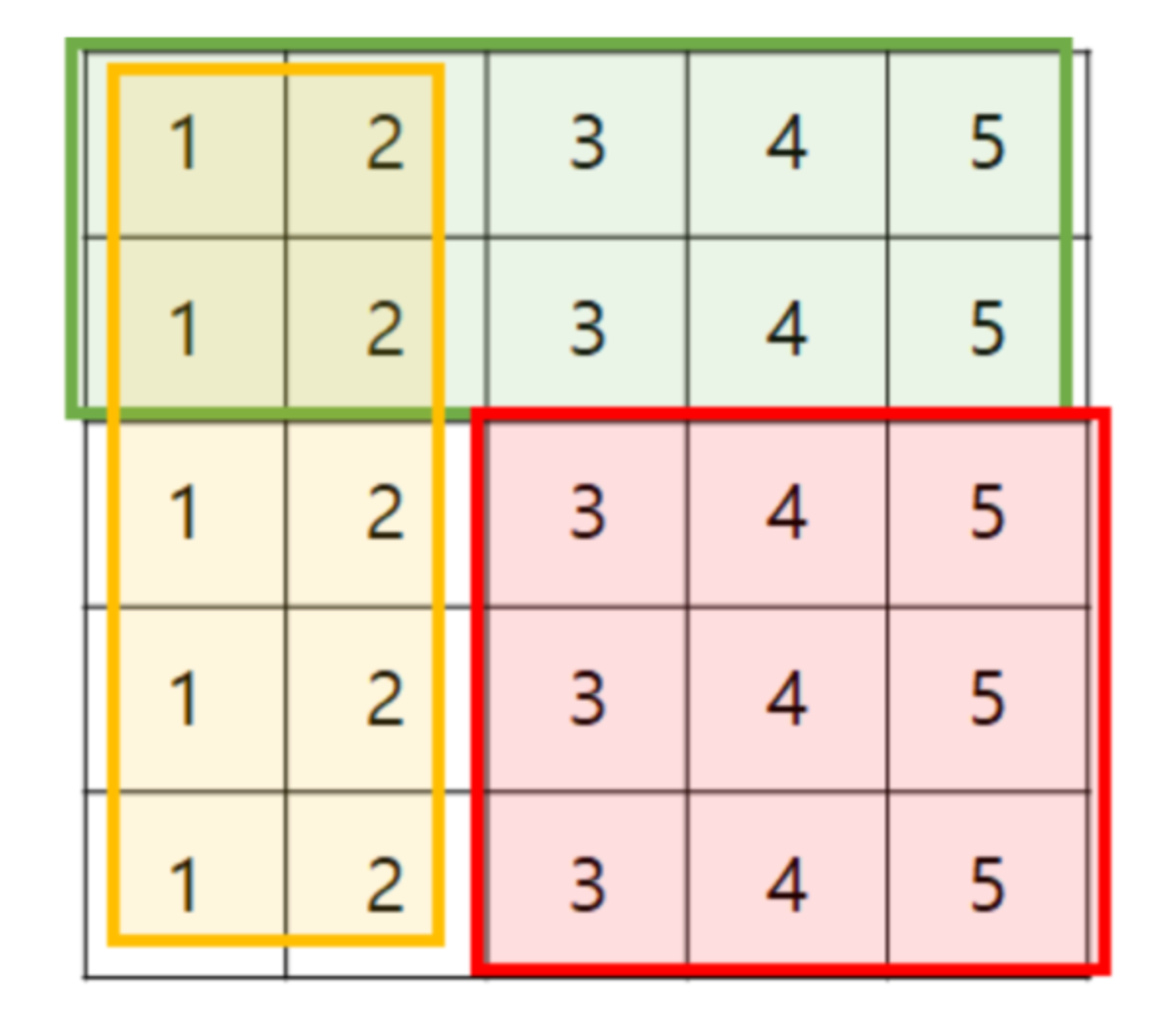
만약 위 그림 처럼 배열을 만들었고 (3,3) 부터 (5,5)의 합을 구하고자 한다.
prefixSum[x][y] 누적합의 상태라면 (5,5)는 전체 합이 될 것이고, 전체 합에서 초록색 부분과, 노란색 부분을 빼주고, 겹치는 부분은 한번 더해주면 (3,3)부터 (5,5)의 누적합을 구할 수 있다.

(3,3) 부터 (5,5)의 구간합 = prefixSum[5][5] - prefixSum[5][3-1] - prefixSum[3-1][5] + prefixSum[3-1][3-1]

구간합 계산식
prefixSum[x2][y2] - prefixSum[x2][y1-1] - prefixSum[x1-1][y2] + prefixSum[x1-1][y1-1]

(N, M)까지 합을 구하는 방법

(N, M) 까지 합을 구하는 방법은 위 계산식과 비슷하게 구할 수 있다.

prefixSum[3][3] = prefixSum[3-1][3] + prefixSum[3][3-1] - prefixSum[3-1][3-1] + array[3][3] 으로 구할 수 있다.

for (int i = 1; i <= n; i++) {  
   for (int j = 1; j <= m; j++) {  
      prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + arr[i][j];  
   }  
}

1. 2차원 구간의 합을 직접 for문을 돌려 구하는 경우 = O(NM+QNM)
2. 1차원 누적합을 각 행마다 계산하는 경우 = O(NM+QN)
3. 2차원 누적합 사용 = O(NM+Q)