Algorithm

에라토스테네스의 체는 소수 구하고자 할 때 사용되는 알고리즘이다. 에라토스테네스의 체 원리 구하고자 하는 소수의 범위만큼 1차원 배열을 생성한다. 2부터 시작하고 현재 숫자의 배수의 해당하는 수를 끝까지 탐색하면서 지운다. (현재 숫자는 지우지 않는다.) 이미 지워

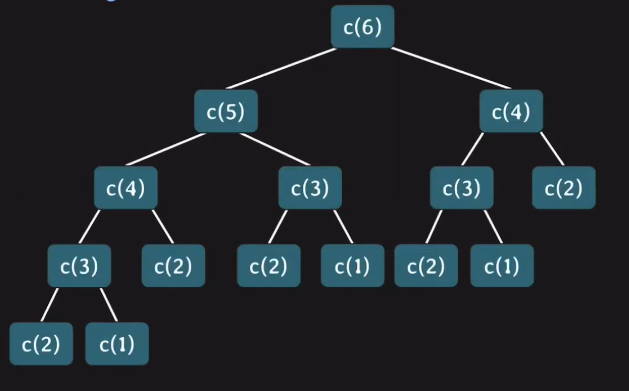
다이나믹 프로그래밍 다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법이다. 이미 계산된 결과는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다. 다이나믹 프로그래밍의 구현은 일반적으로 TopDown (하향식), Bo

누적합(구간합) 은 말 그대로 구간의 누적합을 구하는 문제이다.배열에 값을 저장하고 지정된 인덱스부터 하나씩 더해가는 방식은 최악의 경우 O(n^2)의 시간 복잡도를 갖기 때문에 입력의 범위가 클 때 사용할 수 없다. 하지만 누적합을 사용하면 O(n)으로 해결할 수 있

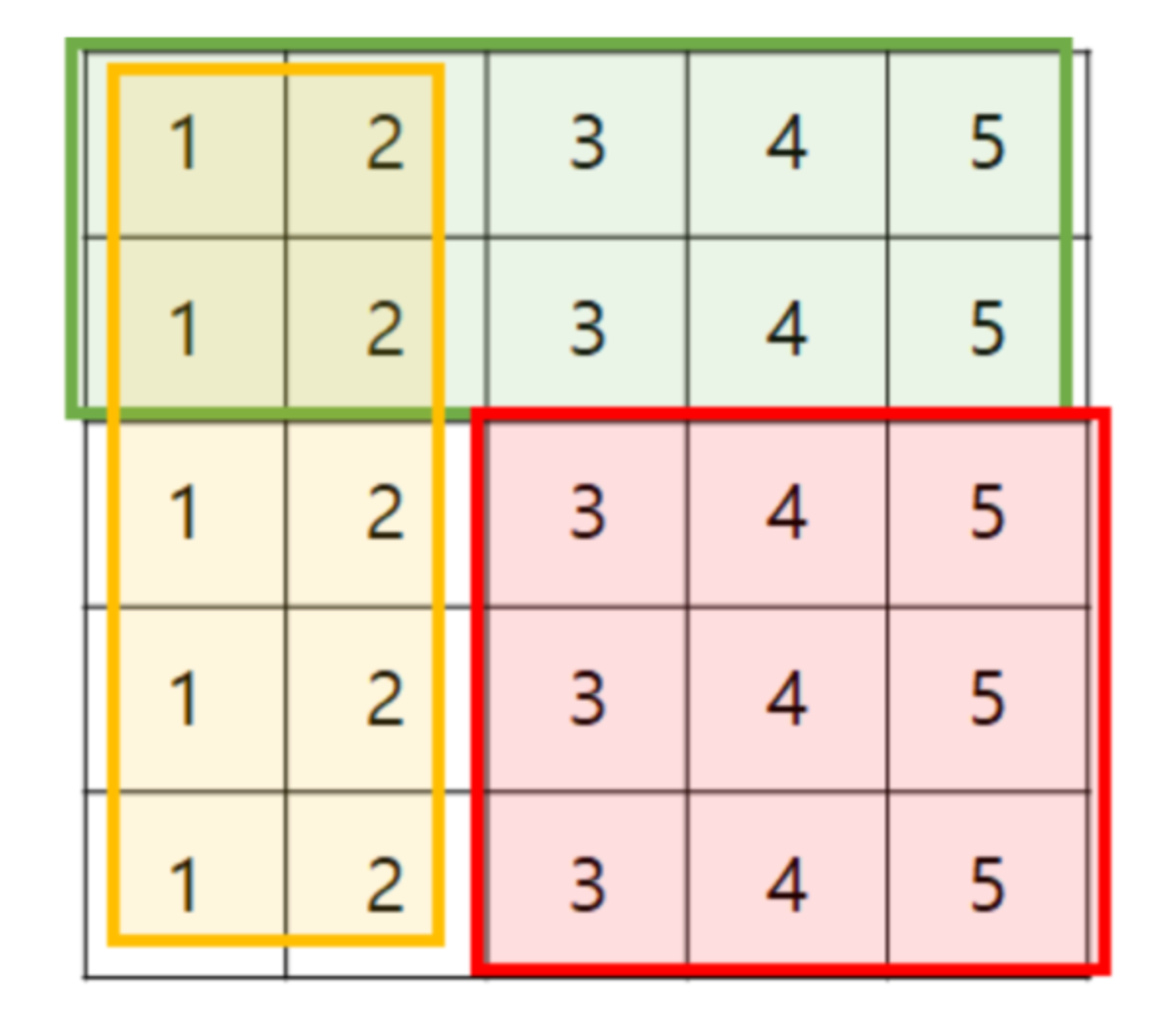
2차원 누적합은 2차원 배열의 누적합을 구할 때 사용한다.N \* M 배열에서 N이 최대 1만, M이 최대 1만, 질문의 수가 10만이라고 할 때2차원 구간의 합을 직접 for문으로 구하는 경우일반적으로 구간합을 구하려면 시간 복잡도는 O(NM + QNM) = O(QN

비트 마스크는 알고리즘이 아닌 하나의 기법으로 정수를 이진수로 표현 하고, 비트 연산 으로 문제를 해결하는 방법이다.예를 들어 알파벳이 아래와 같이 있다고 가정해보자.이 중 a, b, c를 가지고 있다면 위와 같이 표현할 수 있다. 가지고 있는 경우를 1, 가지고 있지

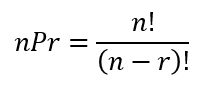
순열이란, 임의의 집합을 순서를 부여하여 차례로 나열하는 것을 말한다.예를 들어 집합 {1, 2, 3} 중 2개의 원소를 선택한 순열을 구하면 {12, 13, 23, 21, 31, 32} 6가지가 나온다.순열의 경우의 수를 일반화하면, n개의 수 중 r개를 선택 하는

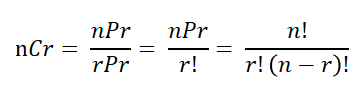
조합 알고리즘은 주어진 n개의 값 중 r개의 값을 순서를 고려하지 않고 나열한 경우의 수이다.순열과 유사하지만 순열은 순서를 고려한다.조합은 주어진 집합에서 원하는 개수로 만들 수 있는 모든 부분 집합을 생성하는 알고리즘이다.순서는 중요하지 않고, 중복을 허용하지 않는

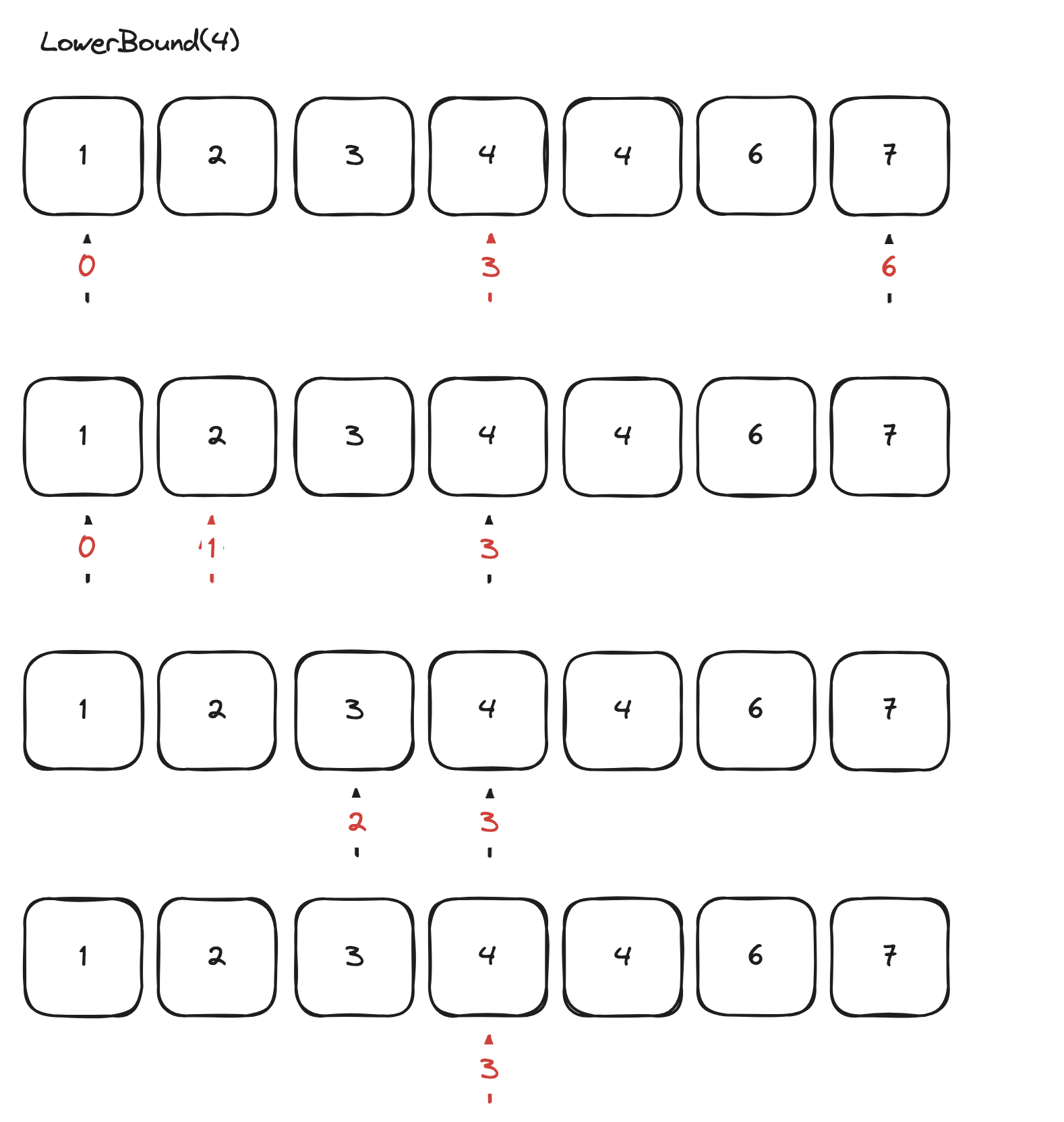
이분 탐색은 데이터 집합에서 원하는 값을 효율적으로 찾는 알고리즘이다.정렬된 배열이나 리스트에서 사용되며, 원하는 값과 현재 검사 중인 값의 중간값을 비교하여 데이터를 반으로 나누어 탐색한다.이분 탐색의 시간 복잡도는 O(log n) 으로 매우 효율적인 검색 알고리즘이

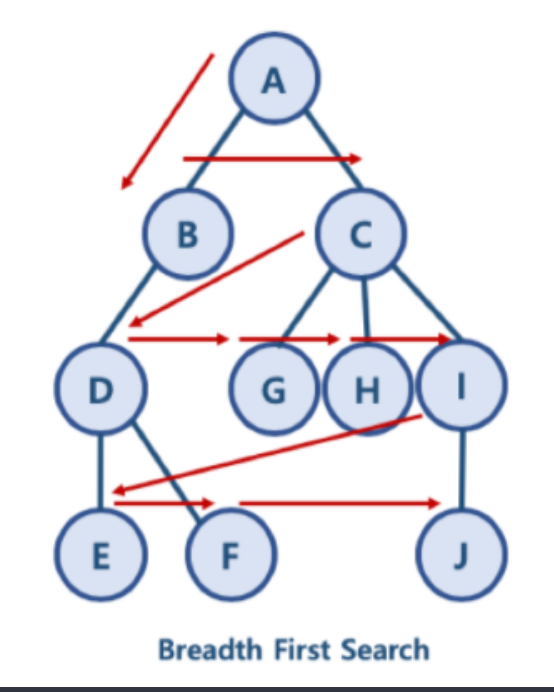
최대한 깊이 내려간 뒤, 더이상 깊이 갈 곳이 없을 경우 옆으로 이동루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기로(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식을 말한다.미로 찾기 할 때, 최대한 한 방향으로 갈 수 있을 때까지 쭉 가