DP
Dynamic Programming은 Optimization Problem을 해결하는 전략 중 하나
- DP는 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법이다.
- 작은 문제(sub problem)의 최적의 해(optimal solution) 을 활용하여 문제의 최적의 해 를 찾는 방식
- 이미 계산된 결과는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다. (동일한 작은 문제는 패스)
Optimization Problem
- Optimization Problem이란 문제를 해결 하는 최적의 답(Optimal Solution)을 찾아야 하는 문제
- 최적의 답은 하나 이상일 수 있다.
- maximum or minimum value 를 가지는 solution을 찾는 문제가 주이다.
- ex) 가장 빨리 도착하는 경로의 소요 시간? (경로 - solution, 소요 시간 - value)
접근 방식
다이나믹 프로그래밍의 구현은 일반적으로 Top-Down (하향식), Bottom-Up (상향식) 으로 구성된다.
| Top-Down | Bottom-Up | |
|---|---|---|
| 구조 | recursive(재귀) | iterative(반복문) |
| subproblem 결과 저장 | memoization | tabulation |
| 주로 사용되는 문제 | sub problem 일부만 계산해도 최종 최적의 해를 구할 수 있을 때 | 모든 sub problem 을 계산해야 최종 최적의 해를 구할 수 있을 때 |
설계 순서
- 주어진 문제의 Optimal Solution이 구조적으로 어떤 특징을 가지고 있는지 분석
- 재귀 형태로 Optimal Solution의 Value를 정의
- 주로 bottom-up 방식으로 optiomal solution의 value를 구한다.
- Optimal Solution을 구해야 한다면 지금까지 계산된 정보를 바탕으로 구한다.
Top-Down
DP의 Top-Down 방식은 재귀함수에 메모이제이션 기법이 적용된 방법
메모이제이션
- 한 번 계산한 결과를 메모리 공간에 메모하는 기법이다.
- 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져온다.
- 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 한다.
Bottom-Up
DP의 Bottom-Up 방식은 가장 작은 문제부터 답을 찾아 가면서 전체 문제의 답을 구하는 방식이다.
보통 반복문으로 구현한다. 재귀 호출을 하지 않으므로 시간과 메모리 사용량이 상대적으로 적다.
예시 - Climbing Stairs
정상을 오르는 데 n번의 스텝이 필요한 계단이 있다. 한 번에 한 스텝 혹은 두 스텝을 오를 수 있을 때, 정상까지 오르기 위해 몇 개의 유니크한 방법이 있는지 구하시오.
문제 분석
총 몇 개의 유니크한 방법 = 최대 몇 개의 유니크한 방법이 있는지
정상에 오르기 직전에는 어느 위치에 있을까?
n은 n-1 위치거나 n-2 위치 일 것이다.
그렇다면 n 은 n-1 에 도달하기 위한 방법의 수 + n - 2 에 도달하기 위한 방법의 수
f(n) = f(n-1) + f(n-2)
문제 해결 방법
재귀
public int climb(int n){
if (n <= 2) return n;
return climb(n-1) + climb(n-2);
}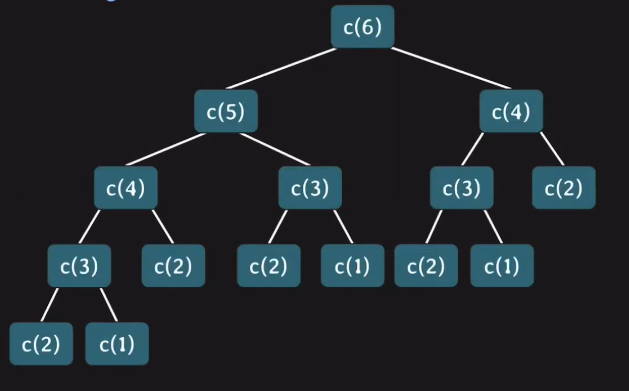
위 그림을 보면 겹치는 Sub Problem이 많기 때문에 결과를 메모해두고 재사용한다.
Top-Down
int memo = {}
public int climb(int n){
if (memo[n] != 0) return dp[n];
if (n <= 2) return n;
dp[n] = climb(n - 1) + climb(n - 2);
return dp[n];
}
Bottom-Up
int[] dp = new int[n];
dp[1] = 1;
dp[2] = 2;
public int climb(int n){
for(int i = 3; i < n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}