Hypothesis Test 2 (t-test)

Student t-test

모집단의 분산과 표준편차를 알지 못할 때 사용되는 통계적 검정 방법으로, 표본에서 추정된 분산이나 표준편차를 활용하여 검정

t검정을 위한 가정
1. 종속변수는 양적변수여야 한다.
2. 모집단의 분산과 표준편차를 알 수 없다.
(모집단의 분산과 표준편차를 알 때는 정규분포로 검정 - 가장 큰 차이점)
3. 모집단의 분포는 정규분포를 따른다.
4. 등분산성의 가정이 충족되어야 한다.

• One Sample t-test

  1개의 sample 값들의 평균이 특정값과 동일한지 비교

검정통계량

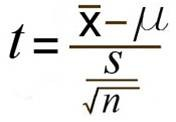
위 통계치는 평균을 빼고, 표준편차로 나눠줬는데 이러한 과정을 정규화라고 하며, 이 과정을 하게 되면 주어진 데이터가 평균은 0, 표준편차가 1인 데이터로 scaling이 됨

T-test 과정

1) 귀무 가설 (Null Hypothesis) 를 설정 (p = 0.5)

$H_0: \mu = \bar{x}$

$\mu =$ 모집단의 평균

$\bar{x} =$ 표본의 평균

2) 대안 가설 (Alternative Hypothesis) 를 설정 (p != 0.5)

$H_1: \mu \neq \bar{x}$

3) 신뢰도를 설정 (Confidence Level) : 모수가 신뢰구간 안에 포함될 확률 (보통 95, 99% 등을 사용)

신뢰도 95%의 의미

= 모수가 신뢰 구간 안에 포함될 확률이 95%

= 귀무가설이 틀렸지만 우연히 성립할 확률이 5% (alpha)

4) P-value를 확인

P-value
주어진 가설에 대해서 "얼마나 근거가 있는지"에 대한 값을 0과 1사이의 값으로 scale한 지표
p-value가 낮다는 것은, 귀무가설이 틀렸을 확률이 높음

5) 이후 p-value를 바탕으로 가설에 대해 결론을 내림

• Two Sample T-test

  2개의 sample 값들의 평균이 서로 동일한지 비교

1) 귀무가설 : 두 확률은 같다 (차이가 없다).

$H_0: \bar{x}_1 = \bar{x}_2$

2) 대안가설 : 같지 않다

$H_1: \bar{x}_1 \neq \bar{x}_2$

3) 신뢰도 : 95%

4) p-value가 (1-Confidence)보다 낮은 경우, 귀무가설을 기각하고 대안 가설을 채택함

결론

One-side test vs Two-side test

One side test : 샘플 데이터의 평균이 "X"보다 크다 혹은 작다 / 크지 않다 작지 않다. 를 검정하는 내용

Two side (tail / direction) test : 샘플 데이터의 평균이 "X"와 같다 / 같지 않다. 를 검정하는 내용