Hypothesis Test 2 (chi-square test)

t-test 는 그룹의 평균값에 대해서 비교하는 가설검정방법

t-test를 사용하기 위해서는 몇가지 조건이 가정되어야 한다.

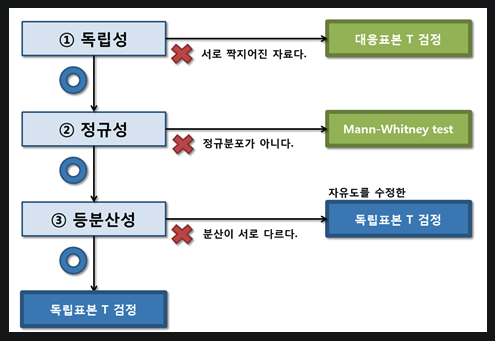
독립성 : 두 그룹이 연결되어 있는 (paired) 쌍인지
등분산성 : 두 그룹이 어느정도 유사한 수준의 분산 값을 가지는지
정규성: 데이터가 정규성을 나타는지

Non parametric methods

모집단이 특정 확률 분포 (normal과 같은)를 따른 다는 전제를 하지 않는 방식
parameter estimation이 필요하지 않기 때문에 non-parametric이라고 부름

Categorical 데이터를 위한 모델링
혹은 극단적 outlier가 있는 경우 매우매우 유효한 방식
distribution free method라고 부르기도 한다.

• Chisquare
• Spearman correlation
• Run test
• Kolmogorov Smirnov
• Mann-Whitney U
• Wilcoxon
• Kruskal-Wallis 등 방법이 존재한다.

$\chi^2$ Tests

one sample test

H0 : Distribution is similar (or specific input)
H1 : Distribution is not similar (or specific input)

주어진 데이터가 특정 예상되는 분포와 동일한 분포를 나타내는지 에 대한 가설검정

Goodness of Fit test라 부르기도 함

예상 되는 빈도의 값은 :

χ2 통계치 의 계산식

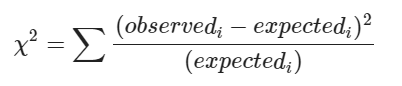
통계치 계산의 예시를 들어보겠습니다.

각 차이의 값을 제곱하는 것으로, 모든 값을 양수로 만들고 관측과 예측값의 차이를 더 강조하는 효과가 있습니다.

통계치를 p-value로 변환

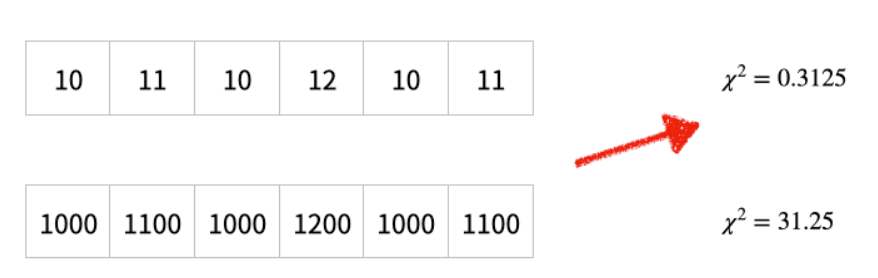
의미는 비슷하지만, 통계치는 여러 이유에 의해서 다릅니다.
따라서 표준화 된 값이 필요합니다!

통계치를 p-value로 변환하려면

stats.chi2.cdf(x2, df)

Two sample χ2 test

H0 : Variable is independent
H1 : Variable is not independent (or specific input)

예측값 계산

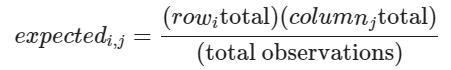
obs = np.array([[9, 4], [7, 2]])

total_obs = np.sum(obs)

exp = np.array([[(9+4)*(9+7), (9+4)*(4+2)], [(7+2)*(9+7), (7+2)*(4+2)]])

exp = exp / total_obs

χ2 통계치 계산

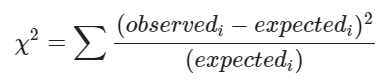
squared = np.power(obs - exp, 2)
squared

array([[0.20661157, 0.20661157],
       [0.20661157, 0.20661157]])

x2 = np.sum(squared / exp)
x2

0.19586894586894588

Scipy를 이용한 χ2 테스트

from scipy.stats import chi2_contingency

print(chi2_contingency(obs, correction = True))  # 파라미터가 True , Yates’ correction 시행함 : pvalue는 약간 다름

print(chi2_contingency(obs, correction = False)) # 위의 계산과 동일한 결과

#결과값
(0.001958689458689457, 0.9646994803686628, 1, array([[9.45454545, 3.54545455],
       [6.54545455, 2.45454545]]))
(0.19586894586894588, 0.6580761824835047, 1, array([[9.45454545, 3.54545455],
       [6.54545455, 2.45454545]]))

chi2_contingency 결과 해석

1 : χ2 statistic
2 : p-value
3 : degree of freedom
4 : expected value for Observed

자유도 (Degrees of Freedom)

해당 parameter를 결정짓기 위한 독립적으로 정해질 수 있는 값의 수

example. 일주일 내내 배라를 가서 콘을 하나씩 먹는 방법

전체 메뉴는 7개만 이라고 가정

월요일 - 7개의 선택 (민초)
화요일 - 6개의 선택 (바닐라)
수요일 - 5개의 선택 (녹차)
목요일 ...
일요일 - 선택지가 없음 🔥 (자유도 X)

따라서 이 문제에 대한 자유도는 n - 1 = 6

---

2-sample χ2 test의 자유도는 1-sample과는 조금 다름

• 1-sample (적합도 검정), DF = # categories-1

• 2-sample (독립성 검정), DF = (#행 - 1)*(#열 - 1)