Linear Algebra

Covariance

Covariance란, 1개의 변수 값이 변화할 때 다른 변수가 어떠한 연관성을 나타내며 변하는지를 측정하는 것

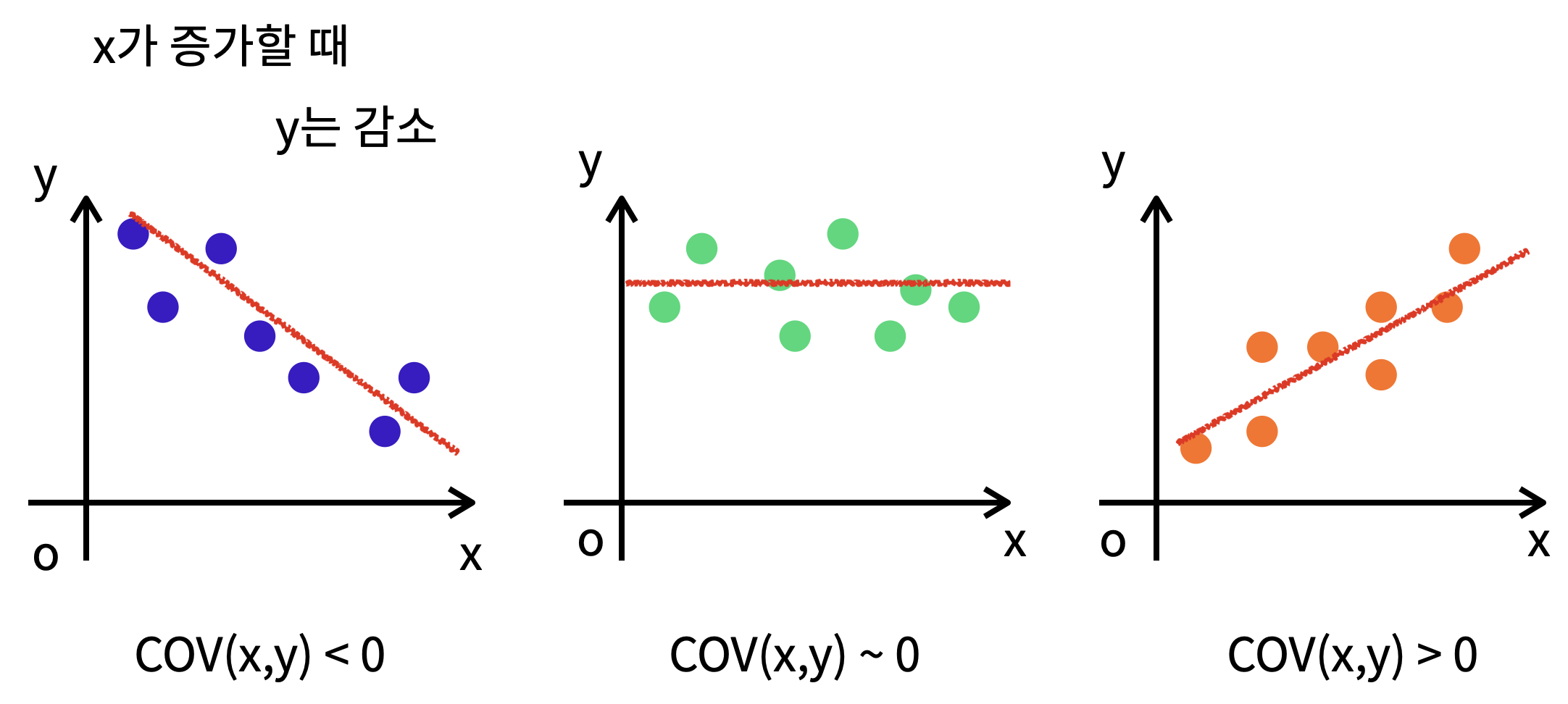
• 첫번째 그래프 : y의 값이 높을때 x 의 값은 낮음. 이는 음의 (negative) 공분산 값을 가짐
• 두번째 그래프 : 양 변수의 높고 낮음에 대하여 관련성을 알 수 없음. 그러므로 이러한 형태는 0에 가까운 공분산 값을 가짐
• 세번째 그래프 : y 값이 낮을때 x의 값도 낮으며, 높을때는 같이 높아짐. 이 경우 양 변수간의 공분산 값은 양의 (positive)값을 가짐

큰 값의 공분산은 두 변수간의 큰 연관성을 나타낸다.

그러나, 만약 변수들이 다른 스케일을 가지고 있다면 공분산은 실제 변수의 연관성에 관계 없이 영향을 받게 될 것이다.

다시 말하면 만약 두 변수가 연관성이 적더라도 큰 스케일을 가지고 있다면, 연관이 높지만 스케일이 작은 변수들에 비해서 높은 공분산 값을 가지게 될 것이다.

Correlation coefficient

공분산을 두 변수의 표준편차로 각각 나눠주면 스케일을 조정할 수 있으며 이를 상관계수라고 함

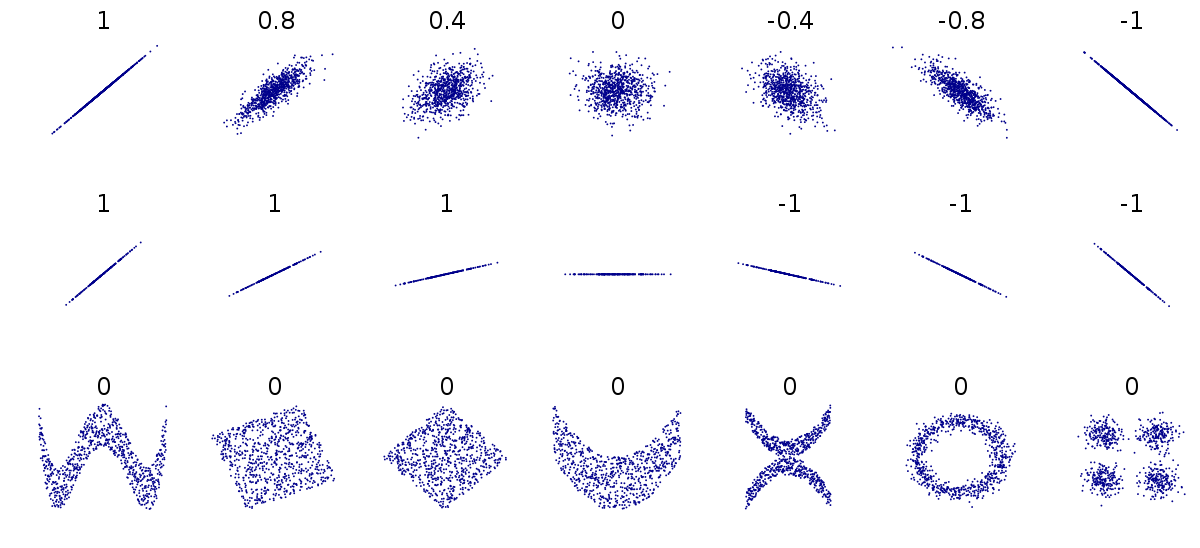
상관계수는 -1에서 1까지로 정해진 범위 안의 값만을 가지며 선형연관성이 없는 경우 0에 근접한다.

대부분의 경우, 상관계수는 공분산에 비해서 더 좋은 지표로써 사용되며 이유는 다음 같다

1. 공분산은 이론상 모든 값을 가질 수 있지만, 상관계수는 -1 ~ 1 사이로 정해져 비교하기가 쉽다
2. 공분산은 항상 스케일, 단위를 포함하고 있지만, 상관계수는 이에 영향을 받지 않는다
3. 상관계수는 데이터의 평균 혹은 분산의 크기에 영향을 받지 않는다

상관계수가 1이라는 것은 한 변수가 다른 변수에 대해서 완벽한 양의 선형 관계를 갖고 있다는 것을 의미

Orthogonality

Orthogonality란, 벡터 혹은 매트릭스가 서로 수직으로 있는 상태

좌표상에 있는 거의 모든 벡터는 다른 벡터와 상관이 아주 작게라도 있다.
하지만 딱 하나, 수직인 벡터만 상관 관계가 전혀 없다.

벡터의 orthogonality 확인
임의의 두 벡터의 내적값이 0이라면 서로 수직으로 배치되어 있다.

단위 벡터 ( Unit Vectors )

선형대수에서, 단위 벡터란 "단위 길이(1)"를 갖는 모든 벡터

Span

Span 이란, 주어진 두 벡터의 (합이나 차와 같은) 조합으로 만들 수 있는 모든 가능한 벡터의 집합

선형 관계의 벡터 (Linearly Dependent Vector)

만약 두 벡터가 같은 선상에 있는 경우, 이 벡터들은 선형 관계에 있다고 표현한다.
즉, 이 두 벡터들은 조합을 통해서 선 외부의 새로운 벡터를 생성 할 수 없다.

이러한 벡터의 span은, 평면 공간이 아닌, 벡터가 이미 올려져 있는 선으로 제한된다.

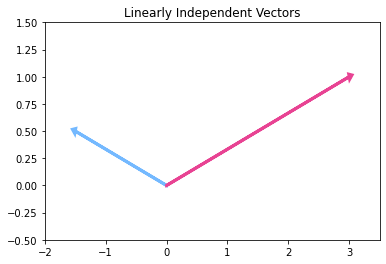
선형 관계가 없는 벡터 (Linearly Independent Vectors)

같은 선상에 있지 않은 벡터들은 선형적으로 독립되어 있다.

주어진 공간 (2개의 벡터의 경우 $\mathbb{R}^2$ 평면)의 모든 벡터를 조합을 통해 만들어 낼 수 있다.

Basis

벡터 공간 $V$의 basis 는, $V$ 라는 공간을 채울 수 있는 선형 관계에 있지 않은 벡터들의 모음 ( span 의 역개념 )

Orthogonal Basis

Orthogonal Basis란, Basis 에 추가로 Orthogonal 한 조건이 붙는, 즉 주어진 공간을 채울 수 있는 서로 수직인 벡터들

Orthonormal Basis

Orthonomal Basis란, Orthogonal Basis에 추가로 Normalized 조건이 붙은 것으로, 길이가 서로 1인 벡터들

Rank

매트릭스의 rank란, 매트릭스의 열을 이루고 있는 벡터들로 만들 수 있는 (span) 공간의 차원

매트릭스의 차원과는 다를 수도 있으며 그 이유는 행과 열을 이루고 있는 벡터들 가운데 서로 선형 관계가 있을 수도 있기 때문이다.

Gaussian Elimination

Gaussian Elimination 은 주어진 매트릭스를 "Row-Echelon form"으로 바꾸는 계산과정 (Rank를 확인하는 방법 중 하나)

"Row-Echelon form"이란, 각 행에 대해서 왼쪽에 1, 그 이후 부분은 0으로 이뤄진 형태

example )

맨 마지막 줄이 0, 0, 0이다 라는 것은 3개의 행이, 선형 관계가 있다.

따라서 Rank 는 2이며 이는 3x3 매트릭스 이지만 $\mathbb{R}^{3}$ 공간이 아닌 $\mathbb{R}^{2}$ 만을 벡터들로 만들어 낼 수 있음을 의미