Vectors and Matrices

Matrix Calculation

Matrix multiplication

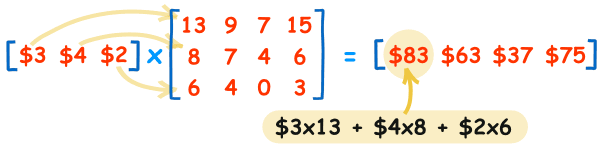
Determinant

2x2

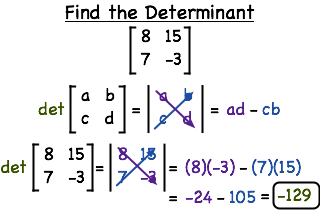
3x3

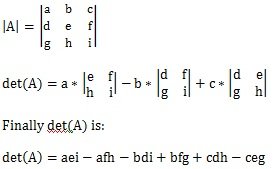
Regression

Linear regression with Scipy

from scipy import stats
stats.linregress([1, 3, 5, 7, 9], [2, 8, 14, 20, 26])

스칼라, 벡터

• 스칼라와 벡터는 선형 대수를 구성하는 기본 단위
• 스칼라는 단순히 변수로 저장되어 있는 숫자이며 벡터 혹은 매트릭스에 곱해지는 경우 해당 값에 곱한 값으로 결정
• 벡터는 파이썬에서는 주로 list로 사용 되며, 데이터프레임의 행/열로써 사용되기도 함
• 매트릭스는 벡터의 모음으로 간주 될 수도 있기 때문에 벡터를 이해하는 것은 매우 중요

스칼라

단일 숫자이며, 변수에 저장 할때는 일반적으로 소문자를 이용하여 표기
스칼라는 실수와 정수 모두 가능

벡터

n 차원의 벡터는 컴포넌트라 불리는 n개의 원소를 가지는 순서를 갖는 모음 (컴포넌트는 스칼라로 간주 되지 않음)
벡터는 일반적으로 위의 화살표 (→) 를 갖는 소문자의 형태로 표현 ($\vec{v}$)

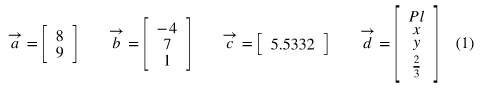
벡터의 크기 (Magnitude, Norm, Length)

벡터의 Norm 혹은 Magnitude는 단순히 길이(선)이므로 피타고라스로 길이를 구할 수 있다.

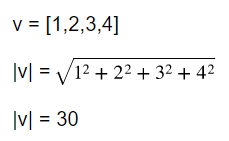
벡터 크기의 특징

벡터의 내적 ( Dot Product )
두 벡터 $\vec{a}$ 와 $\vec{b}$ 의 내적은, 각 구성요소를 곱한 뒤 합한 값과 같음

v = [1, 2, 3, 4]

x = [5, 6, 7, 8]

v $\cdot$ x = 1 5 + 2 6 + 3 7 + 4 8

= 70

• 내적은 교환법칙이 적용 : $a \cdot b = b \cdot a$
• 내적은 분배법칙이 적용: $a \cdot (b + c) = a \cdot b + a \cdot c$
• 벡터의 내적을 위해서는 두 벡터의 길이가 반드시 동일해야 함

매트릭스

매트릭스란, 행과 열을 통해 배치되어있는 숫자들이다. 매트릭스를 표현하는 변수는 일반적으로 대문자를 사용하여 표기한다.

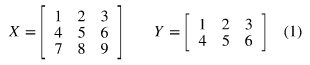
Dimensionality

• 매트릭스의 행과 열의 숫자를 차원 (dimension, 차원수등.)이라 표현
• 차원을 표기 할때는 행을 먼저, 열을 나중에 표기 (행-열)

매트릭스의 일치
2개의 매트릭스가 일치하기 위해서는 다음 조건을 만족해야 함 :

1) 동일한 차원을 보유
2) 각 해당하는 구성요소들이 동일

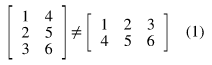
Transpose
행과 열을 바꾸는 것

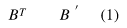
정사각 매트릭스(square matrix)

행과 열의 수가 동일한 매트릭스

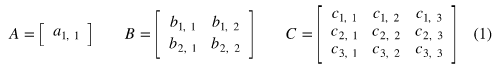
Diagonal (대각): 대각선 부분에만 값이 있고, 나머지는 전부 0

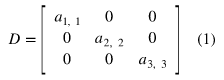
Upper Triangular (상삼각): 대각선 위쪽 부분에만 값이 있고, 나머지는 전부 0

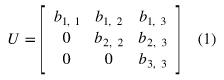
Lower Triangular (하삼각): upper triangular 와 반대로, 대각선 아래에만 값이 있음

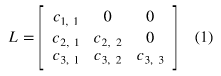
Identity (단위 매트릭스)

Diagonal 매트릭스 중에서, 모든 값이 1인 경우

• 임의의 정사각 매트릭스에 단위 행렬을 곱하면, 그 결과값은 원본 정사각 매트릭스로 나옴
• 반대로 임의의 매트릭스에 대해서 곱했을때 단위 매트릭스가 나오게 하는 매트릭스를 역행렬 (Inverse)이라고 부름

$AI == A$, $AA^{-1} = I$

Symmetric (대칭): 대각선을 기준으로 위 아래의 값이 대칭인 경우

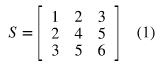
Determinant

행렬식은 모든 정사각 매트릭스가 갖는 속성으로, $det(A)$ 혹은 $|A|$로 표기

2x2 매트릭스를 기준으로, 행렬식은 (AD-BC) 로 계산

Inverse

• 역행렬을 계산하는 방법은 여러가지가 있으며, 행렬의 역수 와 같이 표현 가능
• 행렬과 그 역행렬의 값은 항상 1 (단위 매트릭스)이다.
  2x2 매트릭스를 기준으로, 역행렬을 계산하는 방식중 하나는 아래와 같다:
  
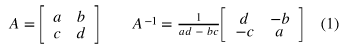
• 매트릭스에 역행렬을 곱하면 단위매트릭스가 된다