Multiple Linear Regression

학습/테스트 데이터로 나누기

모델 학습에 사용한 훈련(train) 데이터를 잘 맞추는 모델이 아니라, 학습에 사용하지 않은 테스트(test) 데이터를 얼마나 잘 맞추는지가 중요하다.

데이터를 훈련/테스트 데이터로 나누어야 우리가 만든 모델의 예측 성능을 제대로 평가할 수 있다.

데이터를 무작위로 선택해 나누는 방법이 일반적이지만,
시계열 데이터를 가지고 과거에서 미래를 예측하려고 하는 경우 무작위로 데이터를 섞으면 절대로 안된다.
이 때는 훈련 데이터 보다 테스트 데이터가 미래의 것이어야 한다.

scikit-learn을 이용해 데이터셋을 분리

from sklearn.model_selection import train_test_split

## X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

from sklearn.linear_model import LinearRegression


# 다중모델 학습을 위한 특성
features = ['a', 'b'] #특성 2개
X_train = train[features]
X_test = test[features]

# 모델 fit
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
mae = mean_absolute_error(y_train, y_pred)

# 테스트 데이터에 적용 
y_pred = model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)

# 훈련 에러(MAE) 계산
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(y_train, y_pred)

# 테스트 에러(MAE)
mae = mean_absolute_error(y_test, y_pred)

해석 및 모델 평가

특성이 2개인 다중선형회귀식 :

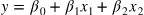
# 절편(intercept)과 계수들(coefficients)
model.intercept_, model.coef_ #coef 2개 나옴

# 회귀식을 만들기
b0 = model.intercept_
b1, b2 = model.coef_

print(f'y = {b0:.0f} + {b1:.0f}x\u2081 + {b2:.0f}x\u2082')

선형회귀는 다른 ML 모델에 비해 상대적으로 학습이 빠르고 설명력이 강하다.
하지만 선형 모델의 이므로 과소적합(underfitting)이 잘 일어난다는 단점이 있다.

회귀모델을 평가하는 평가지표들(evaluation metrics)

• MSE (Mean Squared Error) = $\frac{1}{n}\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$

• MAE (Mean absolute error) = $\frac{1}{n}\sum_{i=1}^{n}\left | y_{i} - \hat{y_{i}} \right |$

• RMSE (Root Mean Squared Error) = $\sqrt{MSE}$

• R-squared (Coefficient of determination) = $1 - \frac{\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}}{\sum_{i=1}^{n}(y_{i} - \bar{y_{i}})^{2}} = 1 - \frac{SSE}{SST} = \frac {SSR}{SST}$

from sklearn.metrics import  mean_squared_error, mean_absolute_error, r2_score

# 회귀방정식 평가지표
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
rmse = mse ** 0.5
r2 = r2_score(y, y_pred)

회귀의 오류지표 설명

• $R^2$ 값이 1에 가까울 수록 데이터를 잘 설명하는 모델이다.
• MAE는 단위 유닛이 같으므로 보다 해석에 용이한 장점이 있다.
• MSE는 제곱을 하기 때문에 특이값에 보다 민감하다.
• RMSE는 MSE를 실제값과 유사한 단위로 변화시켜준다.