
퍼셉트론 (Perceptron)
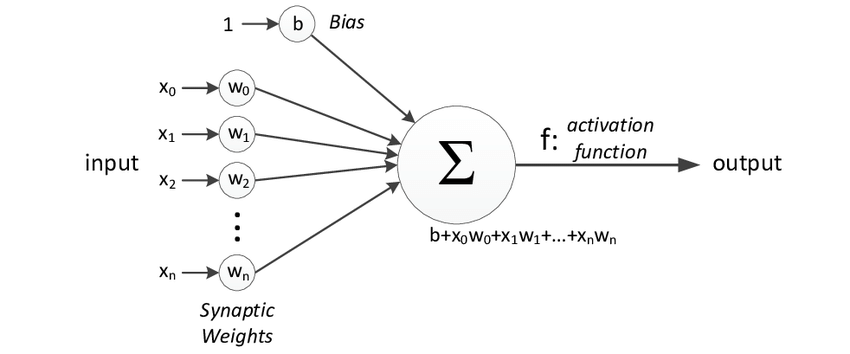
신경망을 이루는 가장 기본 단위인 퍼셉트론 (Perceptron)
다수의 신호를 입력으로 받아 하나의 신호를 출력한다.
- 여기서 신호란 전류나 강물처럼 흐름이 있는 것을 상상하면 된다.
- 전류가 전선을 타고 흐르는 전자를 내보내듯이, 퍼셉트론 신호도 흐름을 만들고 정보를 앞으로 전달한다.
- 다만, 실제 전류와 달리 퍼셉트론 신호는 '흐른다(1)' 또는 '안 흐른다(0)' 두 가지 값을 가진다.
단순한 논리게이트로 본 퍼셉트론
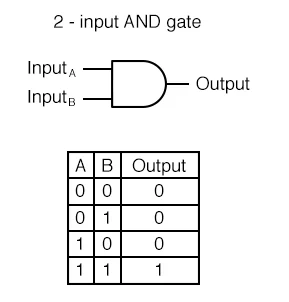
1. AND GATE
입력 신호가 모두 1이어야 1을 출력, 그 외에는 0을 출력한다.
- 파이썬으로 구현
# w1, w2는 가중치(weight)를 의미하는 변수입니다.
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
print(AND(0, 0)) #0을 출력
print(AND(1, 0)) #0을 출력
print(AND(0, 1)) #0을 출력
print(AND(1, 1)) #1을 출력2. NAND GATE
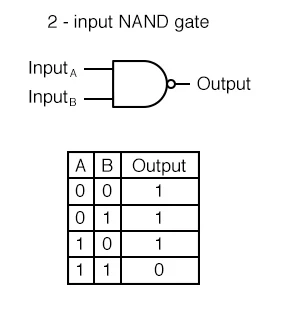
NAND는 Not And를 의미하며, AND GATE의 출력을 뒤집은 것이다.
- 파이썬으로 구현하기
def NAND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 1 ## only change here
elif tmp > theta:
return 0 ## only change hereprint(NAND(0, 0))
print(NAND(0, 1))
print(NAND(1, 0))
print(NAND(1, 1))3. OR GATE
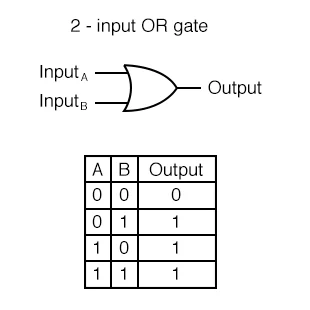
입력 신호가 하나만 1이어도 1을 출력한다.
- 파이썬으로 구현하기
def OR(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.3 ## only change here
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1print(OR(0, 0))
print(OR(0, 1))
print(OR(1, 0))
print(OR(1, 1))퍼셉트론의 한계 ?!
XOR GATE(배타적 논리합)을 표현할 수 없다.
| A | B | OUTPUT |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
퍼셉트론은 직선으로 나뉜 두 영역을 만드는데, 직선 하나로는 XOR을 표현할 수 있는 방법이 없다.
즉, 퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있는 한계가 있다.
AND, NAND, OR 게이트를 적절히 조합하면 XOR을 완성할 수 있다.
위의 단층 퍼셉트론을 조합하여, 즉 층을 쌓아서 XOR GATE를 구현할 수 있다.
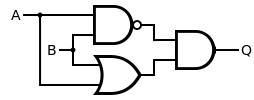
위 이미지를 코드로 구현해보면,
def XOR(x1, x2):
return AND(NAND(x1, x2), OR(x1, x2))이렇게 층이 여러 개인 퍼셉트론을 다층 퍼셉트론(multi-layer perceptron) 이라고 한다.
Reference : 모두의 딥러닝, 밑바닥부터 시작하는 딥러닝
