[시계열] 시계열 분석 basic

전주미·2024년 4월 15일
시계열분석
post-thumbnail

그 어렵다는 시계열분석.
통계지식이 빠삭해야 잘할텐데.
시계열 분석을 내가 진짜 제대로 해본다기보다는 튜토리얼? 한 부분 해봤다고 표현하면 될 것 같다.

시계열 분석을 하려면 일단, jupyter notebook에 들어가서
prophet을 설치해야하는데, 안깔리네.... 후.. 왜 맨날 나만 바로 안돼 !!!!!! 하고 있는데
맥에서는 prophet이 잘 안깔린다는 정보를 얻음..-_-...

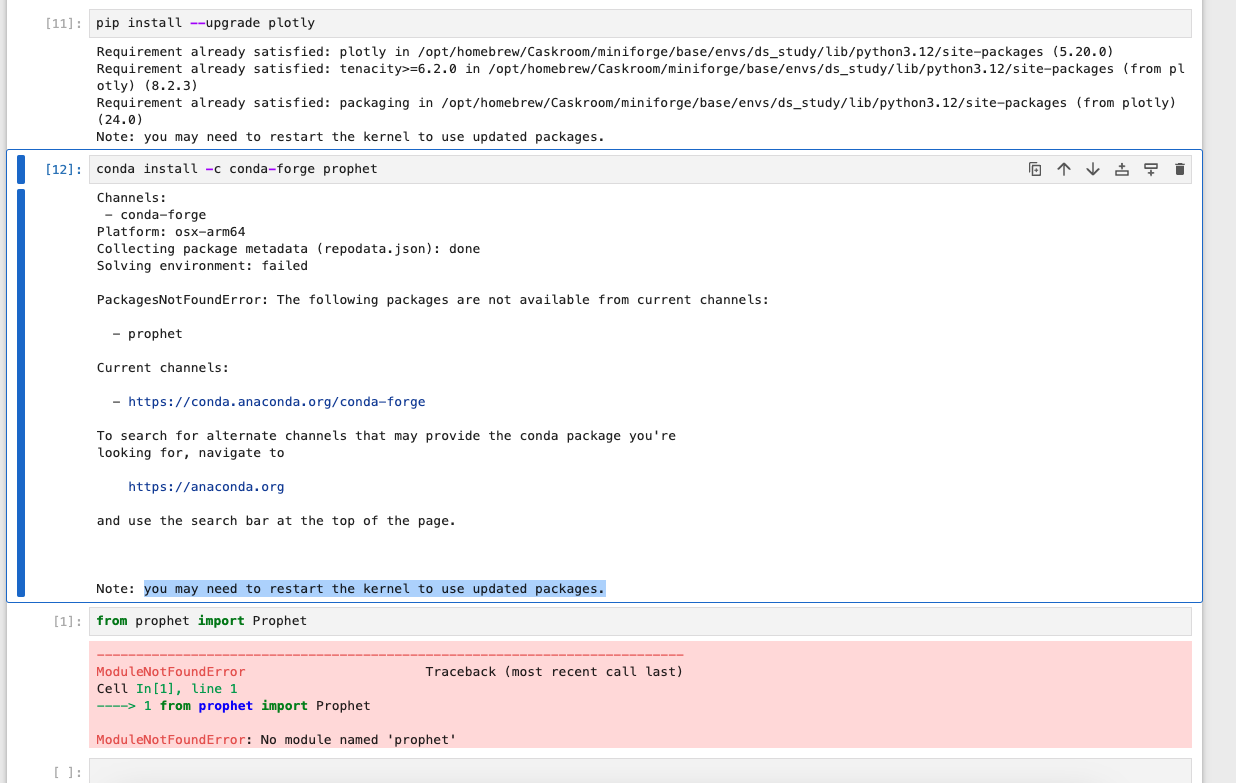
이런 메시지나 뜨고 Note: you may need to restart the kernel to use updated packages.
도저히 해결안됨. 걍 이건 코랩에서 실습해야한다.

!pip install --upgrade plotly
!pip install pandas-datareader
!pip install prophet

순 차적으로 위 모듈을 깔아준다. 코랩에서 하니 아주 잘도 이미 깔려있단다.(현타)

그 다음에 한번 불러와 보자.

from prophet import Prophet
from pandas_datareader import data

오호~ 아무 문제 없이 모듈이 잘 가져와진다.

시계열 분석을 해보기에 앞서서 함수의 기초 개념을 다시 한번 상기시켜보겠다.
왜냐면 이거 모름 그냥 시계열이고 나발이고 아무것도 못해여..

1. def

def test_def(a,b):
  return a + b
c = test_def(2, 3)
c

5

5 + c

10

  • def라고 하는 예약어를 사용합니다.
  • 가장 기초적인 모양의 def 정의이다.
  • 이름(test_df)과 입력 인자(a,b)를 선언해준다.
  • def 함수가 출력해야할 값이 있다면 return 해준다.

2. 전역변수(global), 지역변수(local)

a = 1
#전역변수
def edit_a(i):
  # 지역변수(local)
  global a
  a = i
edit_a(2)
a

2

  • 함수 밖에 값이 하나 있고, 함수 안에 있는 것은 함수밖에 있는 변수를 참조하지 못하는 경우가 많다.
  • global 변수를 def내에서 사용하고 싶다면 global로 선언한다.
  • global사용하면 입력된 i로 a를 바꿀 수 있다.
def edit_a(i):
  a = i
edit_a(5)
print(a)

2

  • def 내에서의 변수와 밖에서의 변수는 같은 이름이어도 같은 것이 아니다.

수학수식 기호로 바꾸는 법은 아래와 같다. 달러 기호를 이용해서 이탤릭체로 바꿀 수 있다.

$$ y = asin(2\pi ft + t_0) + b $$

이렇게 삼각함수가 예쁘게 출력된다.
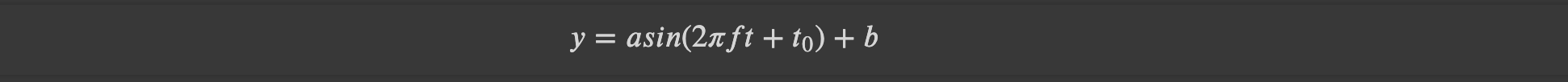삼각함수의 표준형이다.

본격적으로 sin함수의 그래프를 한번 그려보겠다.

1. Sin함수 시계열로 나타내기

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
  • endTime: x축을 어디까지로 정할 것이냐
  • sampleTime: x축을 얼마의 간격으로 나눌 것이냐
  • startTime: x축을 언제로 시작할 것이냐
  • """ """: 함수의 설명을 호출하는 기능
  • np.arange(startTime, endTime, sampleTime) 시작 시간부터 끝나는 시간까지 어떠한 간격으로,
  • result = time을 이용해서 삼각함수를 그대로 다 만들어낸다.
def plotSinWave(amp, freq, endTime, sampleTime, startTime, bias):

  """
  plot sine wave
  y = a sin(2 pi f t + t_0) + b
  """
# 기능을 하나 만들었을때 위와 같이 """ """ 사이에 설명해놓으면,
# plotsineWave() 괄호안에서 Doctrine을 확인하면 """ """ 사이에 써놓은 내용이 그대로 나온다.

  time = np.arange(startTime, endTime, sampleTime)
  result = amp * np.sin(2 * np.pi * freq * time + startTime) + bias

# 그다음 그래프 그리는 코드를 써준다.
  plt.figure(figsize = (12, 6))
  plt.plot(time, result)
  plt.grid(True)
  plt.xlabel("time")
  plt.ylabel("sin")
  plt.title(str(amp) + "*sin(2*pi" + str(freq) + "*t+" + str(startTime) + ")+" + str(bias))
  plt.show()
# 들어갈 인자를 넣어주면,
plotSinWave(2, 1, 10, 0.01, 0.5, 0)
  • 1Hz로 그려라
  • endTime = 10
  • 0.01간격
  • startTime = 0.5 (0.5부터 그려라)
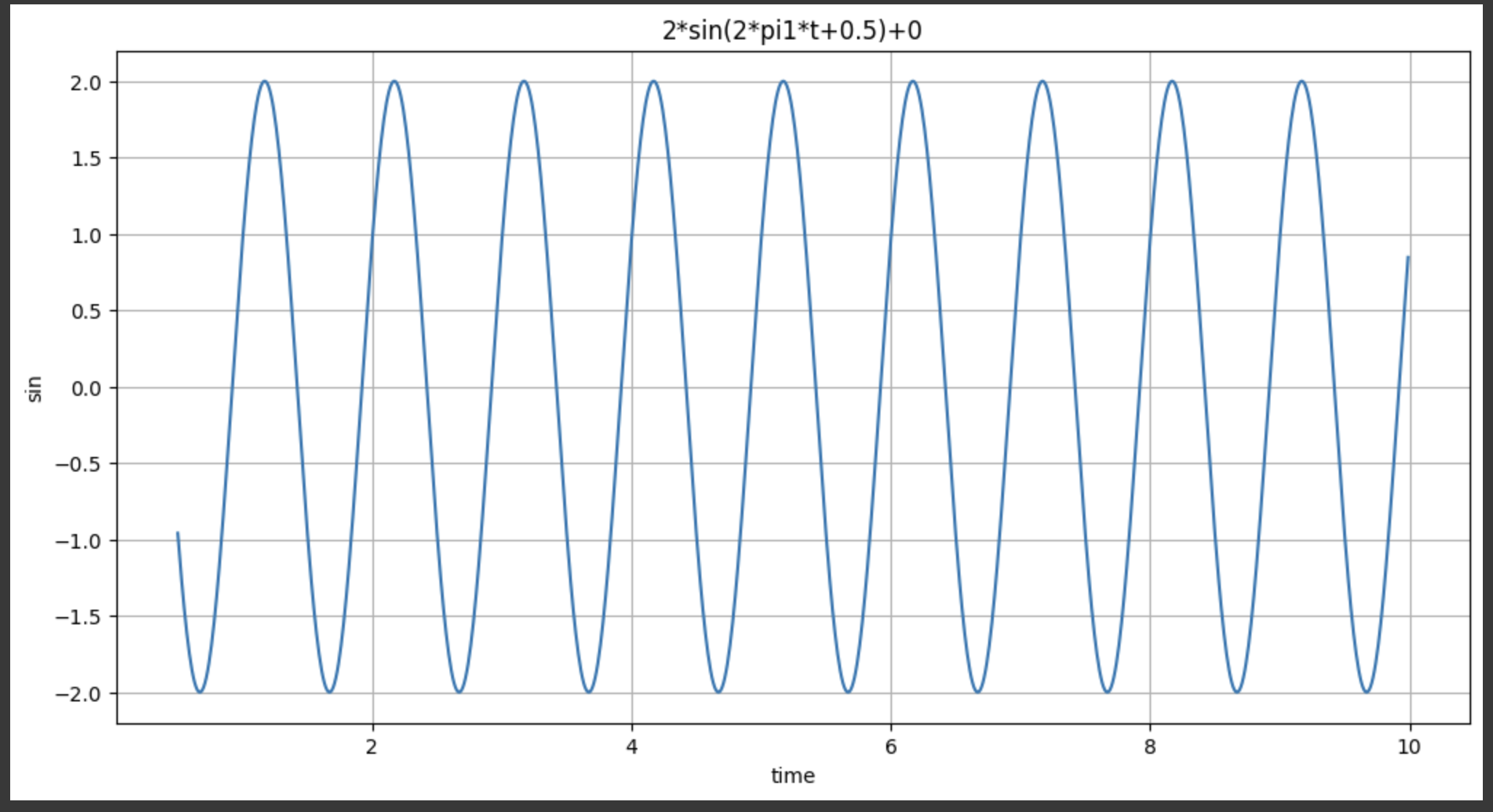    그런데 이렇게 하면, 함수가 너무 어려워지고 내가 어떤 인자를 넣어야하는 지 헷갈리게 된다. 이럴때는?
    위 코드에서 변수를 좀 변경해야겠다.

kwrgs : keyworded arguments 를 사용해주자!

어떠한 누군가, 사용자가 endTime, sampleTime 등을 지정했다면 지정된 값으로 그래프가 그려진다. 만약 지정하지 않았다면 default값이 입력되어 그래프가 그려진다.
즉, plotSinWave() 괄호안에 입력 값을 넣지 않으면, 기본값이 사용되는 것이다.
그리고 plotSinWave() 에서 shift+tab을 누르면 아까 적어두었던 """ """ 내용이 나온다.

def plotSinWave(**kwargs):
  """
  plot sine wave
  y = a sin(2 pi f t + t_0) + b
  """

# 기본값을 설정해서 자동으로 출력이 되게끔한다.
  endTime = kwargs.get("endTime", 1)
  sampleTime = kwargs.get("sampleTime", 0.01)
  amp = kwargs.get("amp", 1)
  freq = kwargs.get("freq", 1)
  startTime = kwargs.get("startTime", 0)
  bias = kwargs.get("bias", 0)
  figsize = kwargs.get("figsize", (12, 6))

  time = np.arange(startTime, endTime, sampleTime)
  result = amp * np.sin(2 * np.pi * freq * time + startTime) + bias

  plt.figure(figsize = (12, 6))
  plt.plot(time, result)
  plt.grid(True)
  plt.xlabel("time")
  plt.ylabel("sin")
  plt.title(str(amp) + "*sin(2*pi" + str(freq) + "*t+" + str(startTime) + ")+" + str(bias))
  plt.show()
plotSinWave()

이렇게 기본값을 설정해 보았을 때, 그래프가 이렇게 나왔다.

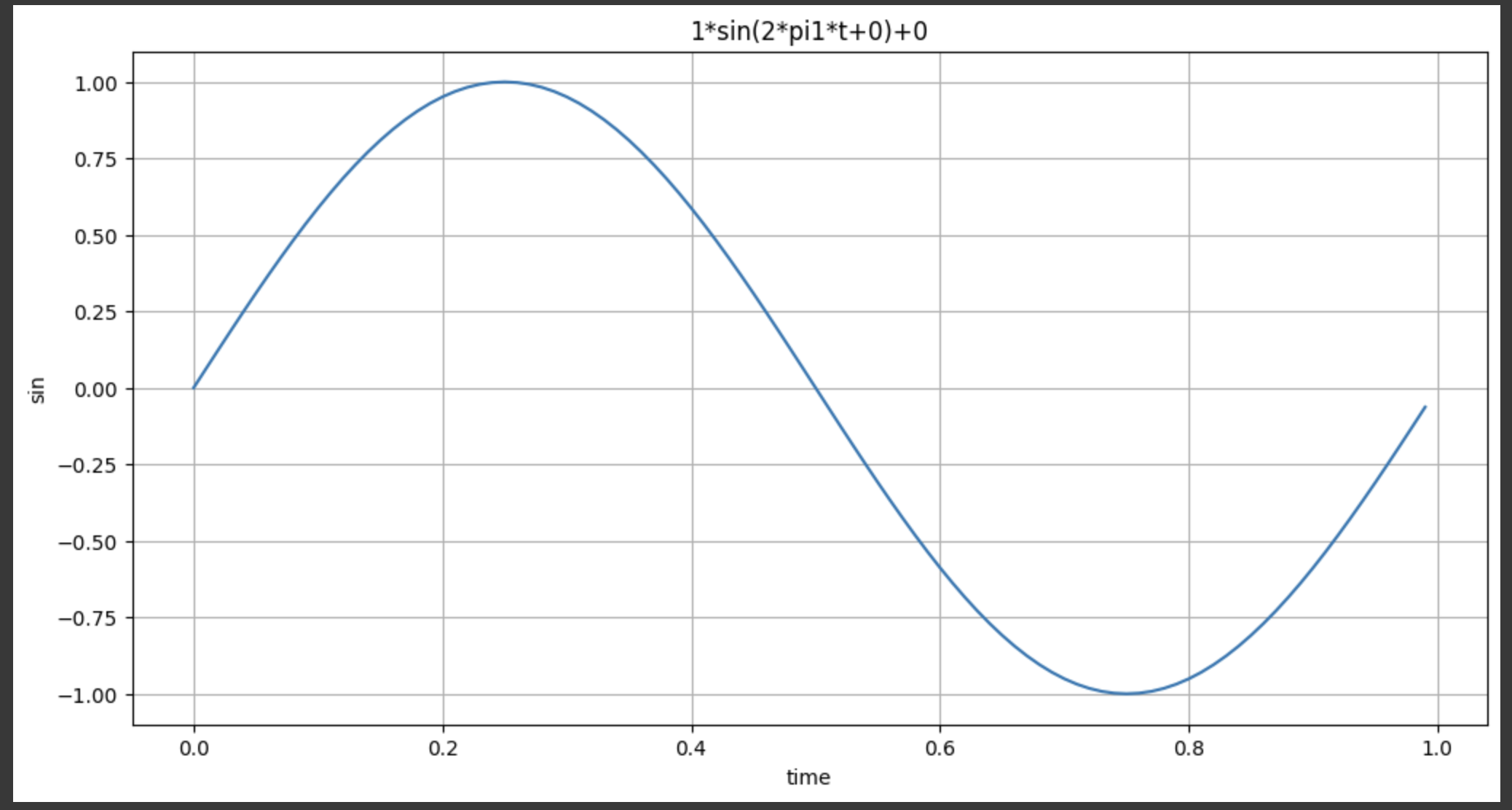
인자값을 조금 바꾸어주면?

plotSinWave(amp=2, freq=0.5, endTime=10)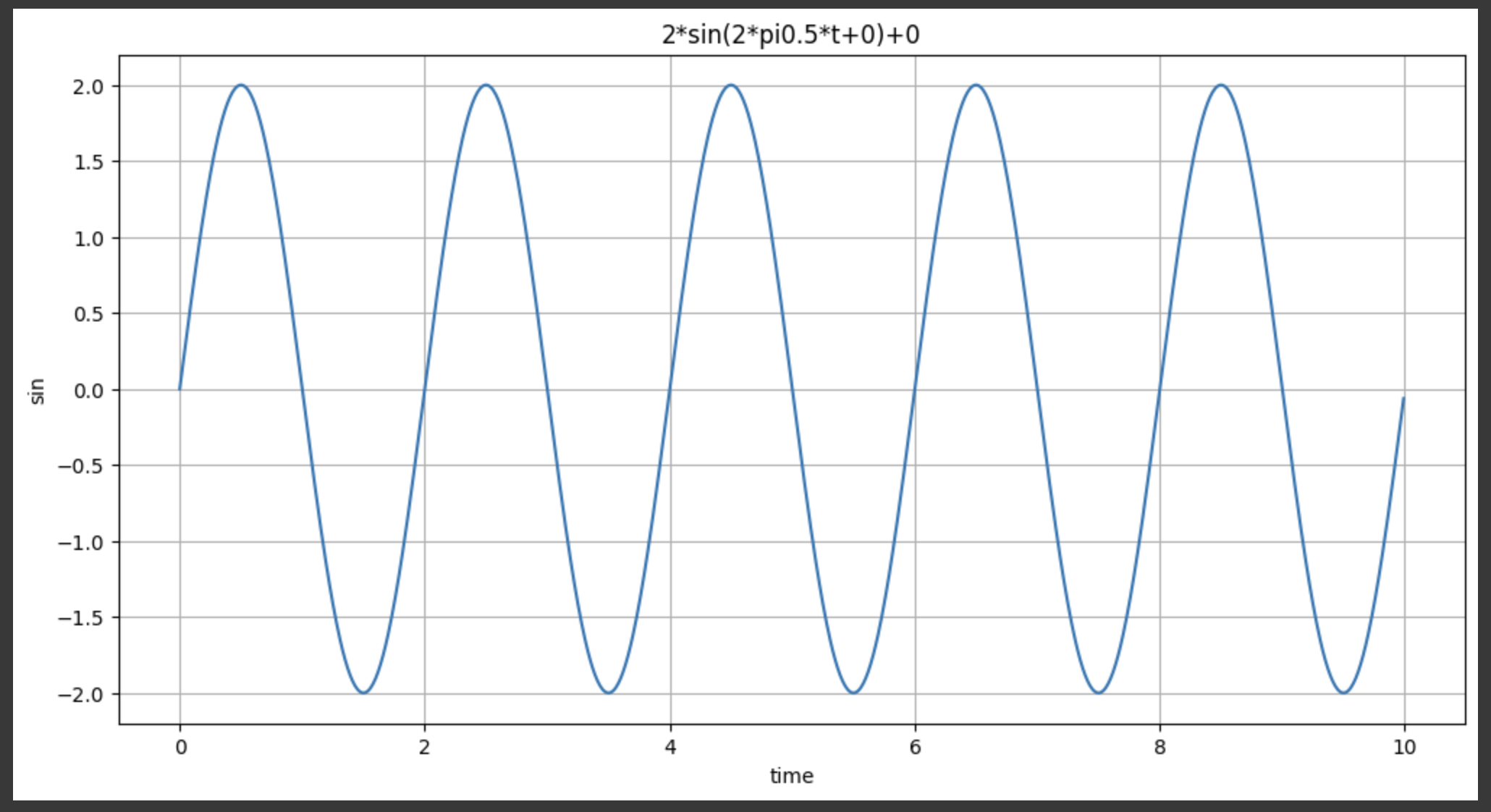

2. 내가 만든 함수 import

내가 만든 함수를 모듈로 만들어 import 해보자.
.py파일을 만들어야한다. vscode를 사용해도되고, 주피터 노트북에서도 가능하다.
if__name__=="__main__": 코드 추가

  • drawSinWave.py
%%writefile ./drawSinWave.py

import numpy as np
import matplotlib.pyplot as plt

def plotSinWave(**kwargs):
  """
  plot sine wave
  y = a sin(2 pi f t + t_0) + b
  """

  endTime = kwargs.get("endTime", 1)
  sampleTime = kwargs.get("sampleTime", 0.01)
  amp = kwargs.get("amp", 1)
  freq = kwargs.get("freq", 1)
  startTime = kwargs.get("startTime", 0)
  bias = kwargs.get("bias", 0)
  figsize = kwargs.get("figsize", (12, 6))

  time = np.arange(startTime, endTime, sampleTime)
  result = amp * np.sin(2 * np.pi * freq * time + startTime) + bias

  plt.figure(figsize = (12, 6))
  plt.plot(time, result)
  plt.grid(True)
  plt.xlabel("time")
  plt.ylabel("sin")
  plt.title(str(amp) + "*sin(2*pi" + str(freq) + "*t+" + str(startTime) + ")+" + str(bias))
  plt.show()

if __name__ == "__main__":
  print("hello world~!!")
  print("this is test graph")
  plotSinWave(amp=1, endTime=2)

실행시켜주면 위와 같이 현재경로의 파일이 생겨난것을 확인 할 수 있다.

따라서 terminal에서 drawSinWave.py를 실행시켜보면, 그래프가 나온다.


주피터 노트북에서 불러오는 것도 가능하다.

import drawSinWave as DS
dS.plotSinWave()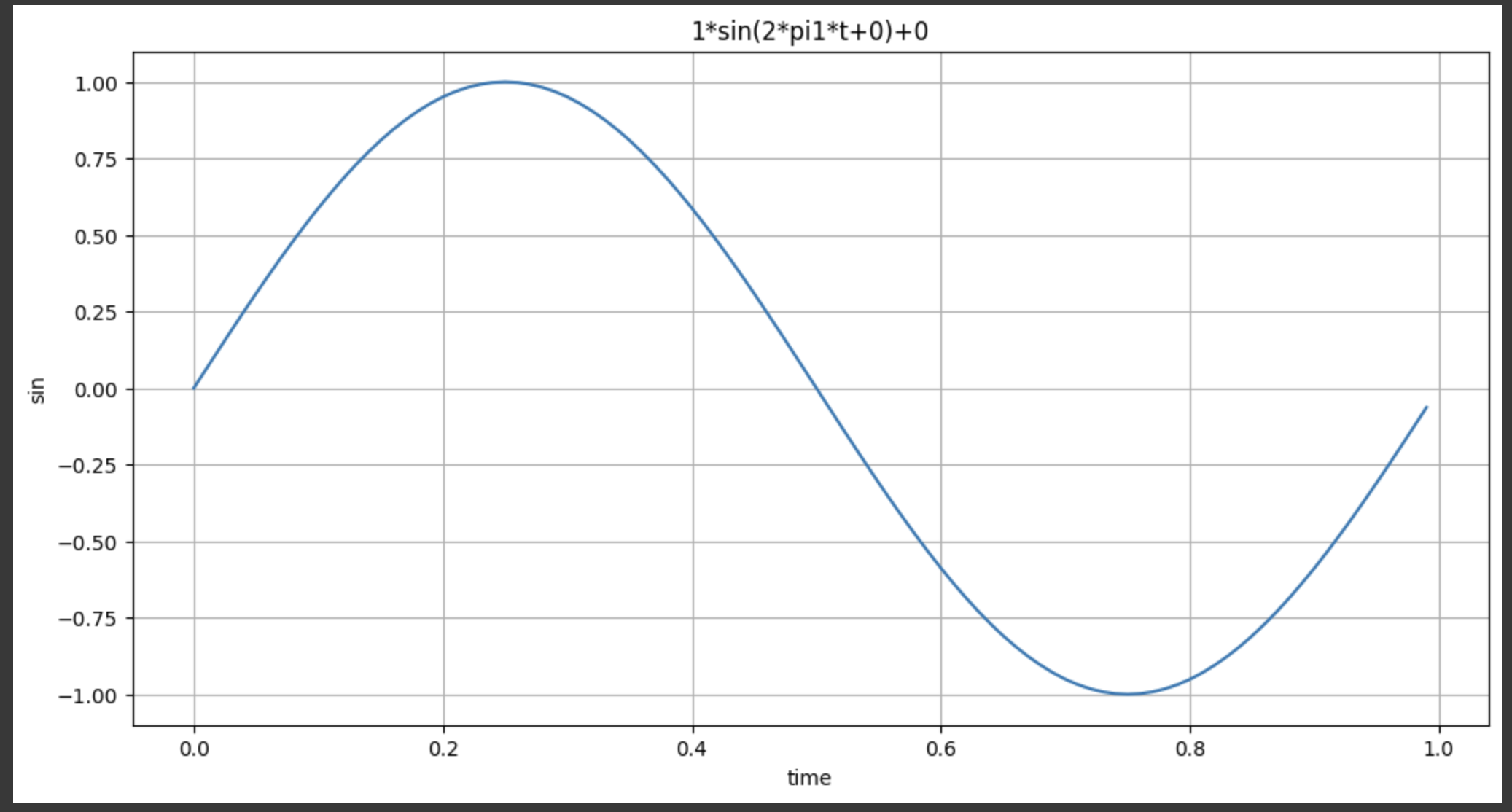

freq를 바꾸어보면,

import pandas as pd
dS.plotSinWave(freq=5)

아래와 같은 그래프가 생성된다.

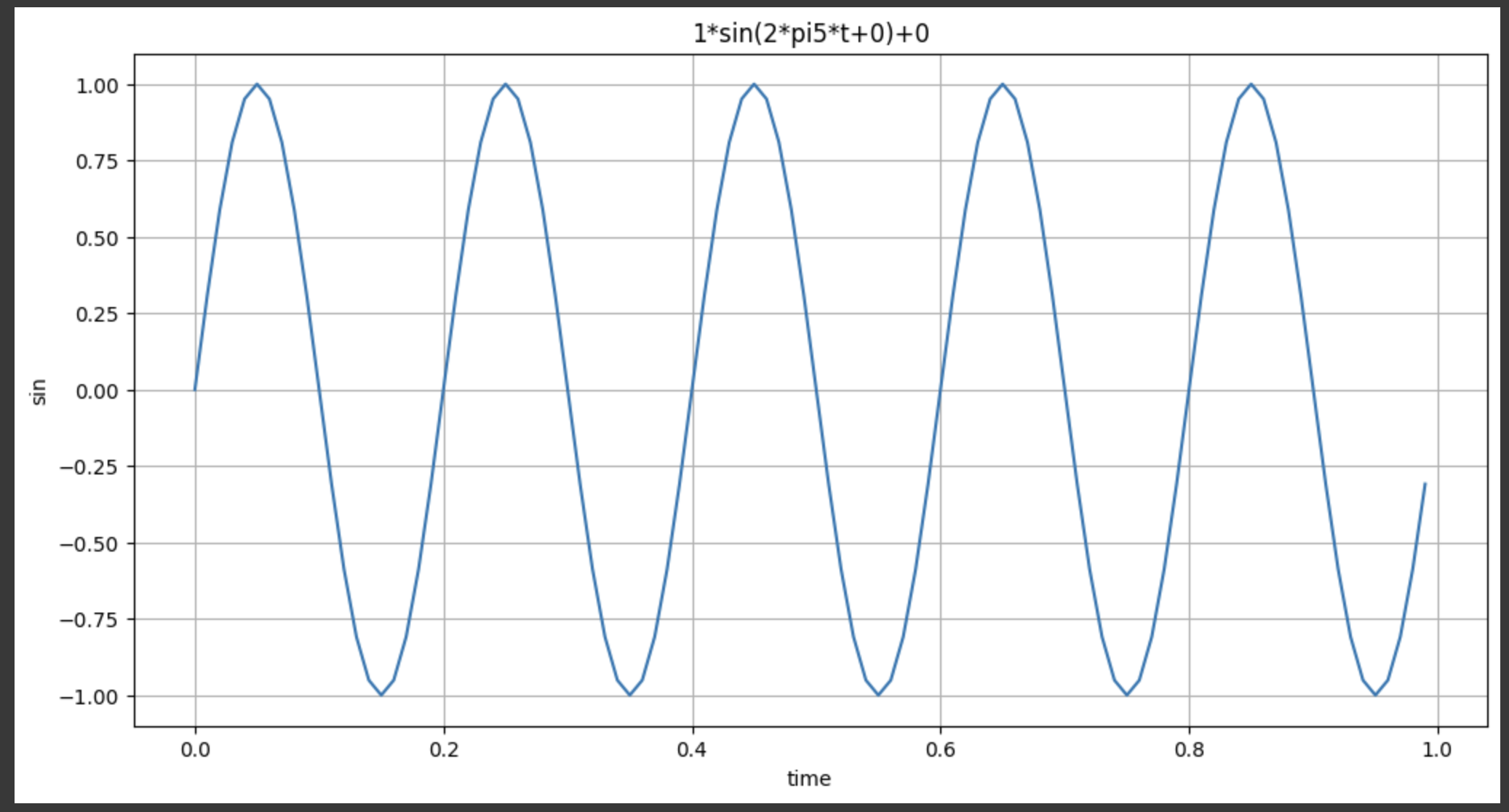
3. 그래프 한글 설정

이번에는 그래프 한글 설정을 모듈화해보겠다.

%%writefile ./set_matplotlib_hangul.py

import platform
import matplotlib.pyplot as plt
from matplotlib import font_manager, rc

path = "c:/Windows/Fonts/malgun.ttf"

if platform.system() == "Darwin": # mac인지 묻는것.
  print("hangul OK in your MAC!!!")
  rc("font", family="Arial Unicode MS")
elif platform.system() == "WINDOWS":
  font_name = font_manager.FontProperties(fname=path).get_name()
  print("hangul OK in your Windows!!!")
  rc("font", family="font_name")
else:
  print("Unknown system..sorry...")

plt.rcParams["axes.unicode_minus"] = False

import set_matplotlib_hangul

원래 이렇게 입력하면 나의 경우 hangul OK in your MAC!!! 이라고 떠야하는데
코랩에서 해서 그런건지.. 알 수 없는 시스템이라고하는 흑흑..

4. prophet 기초

필요한 모듈을 먼저 가져온다.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%maplotilb inline

2년간의 데이터가 어떤 sin특성을 가졌다.

예제 1

time = np.linspace(0, 1, 365*2)
result = np.sin(2*np.pi*12*time)
ds = pd.date_range("2018-01-01", periods=365*2, freq="D")
df = pd.DataFrame({"ds": ds, "y":result})
df.head()
  • D : day
  • ds : column 이름

아래와 같이 이런식의 데이터가 완성되었다. 

df["y"].plot(figsize=(10, 6))

730일 간의 sin그래프를 그려보았다고 쉽게 생각하자!

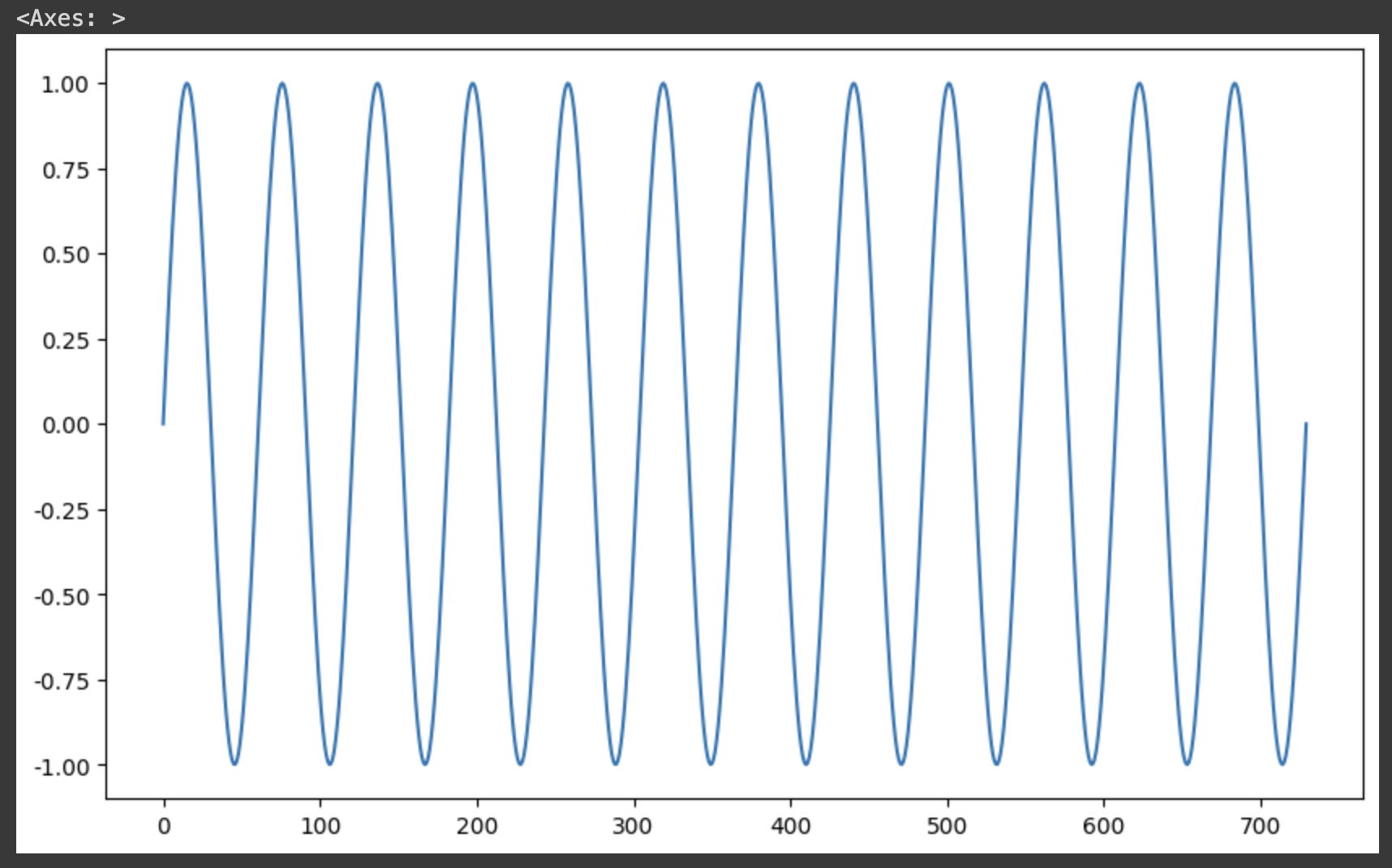
연 주기성, 일 단위로 추적
그 이후 30일간을 예측해봐라

from prophet import Prophet

m = Prophet(yearly_seasonality=True, daily_seasonality=True)
m.fit(df);

앞으로 30일 간의 예측 값

future = m.make_future_dataframe(periods=30)
forecast = m.predict(future)
m.plot(forecast);

점이 없는 파란색 선이 예측 데이터이다.

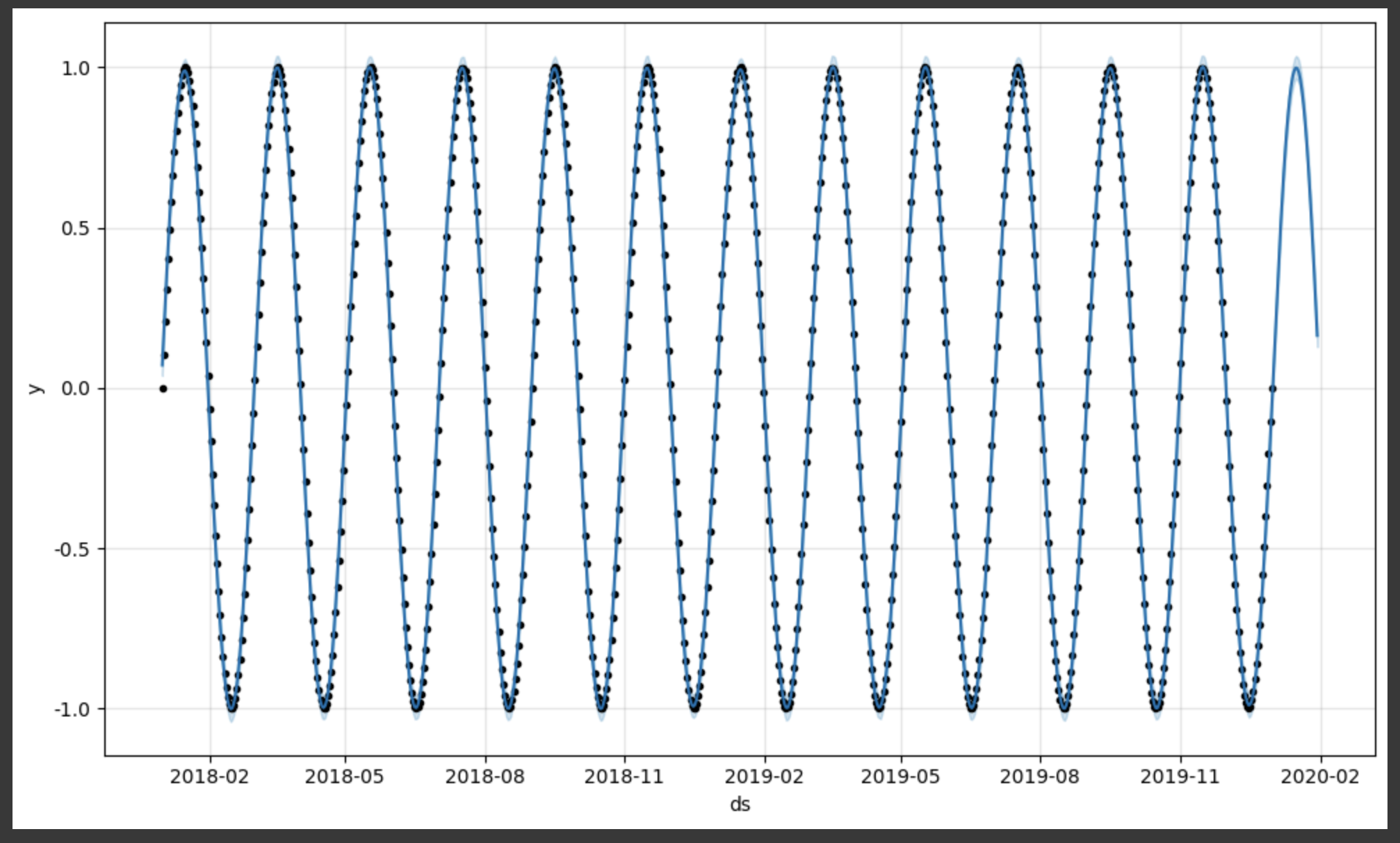
예제 2

데이터 프레임에서 y는 10, 6 사이즈로 만들고, time을 추가해주면 그래프가 위로 올라가는 형태로 나온다.

time = np.linspace(0, 1, 365*2)
result = np.sin(2*np.pi*12*time) + time

ds = pd.date_range("2018-01-01", periods=365*2, freq="D")
df = pd.DataFrame({"ds": ds, "y":result})

df["y"].plot(figsize=(10, 6))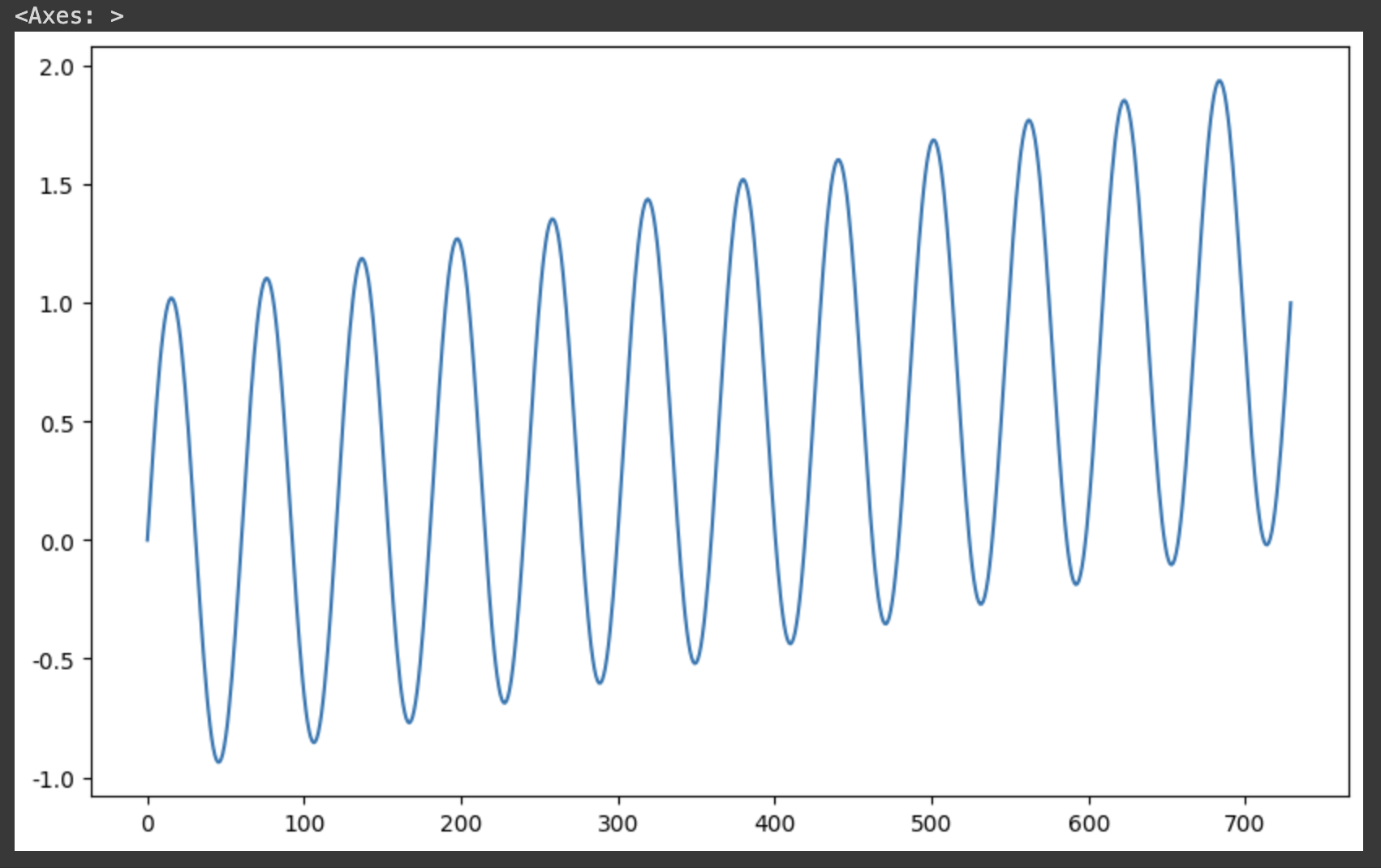

m = Prophet(yearly_seasonality=True, daily_seasonality=True)
m.fit(df)
future = m.make_future_dataframe(periods=30)
forecast = m.predict(future)
m.plot(forecast);

예측한 값을 시각화하면? 아래와 같다.

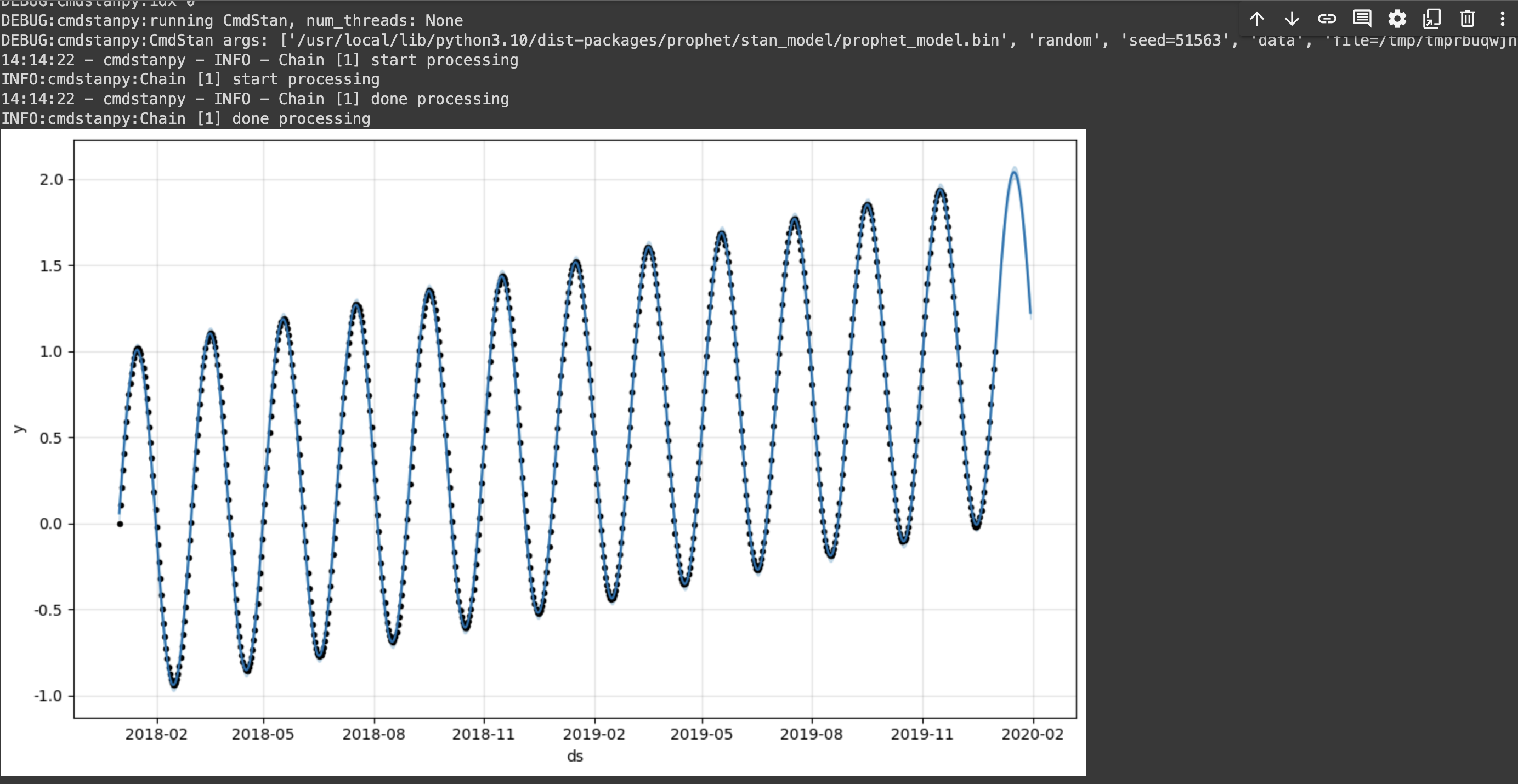
예제 3. 노이즈를 실어 보면?

시간에 랜덤한 수를 넣어 노이즈를 실어보면 불규칙한 에러? 오차가 생긴 데이터 형태로 변한다.

time = np.linspace(0, 1, 365*2)
result = np.sin(2*np.pi*12*time) + time + np.random.randn(365*2)/4

ds = pd.date_range("2018-01-01", periods=365*2, freq="D")
df = pd.DataFrame({"ds": ds, "y":result})

df["y"].plot(figsize=(10, 6))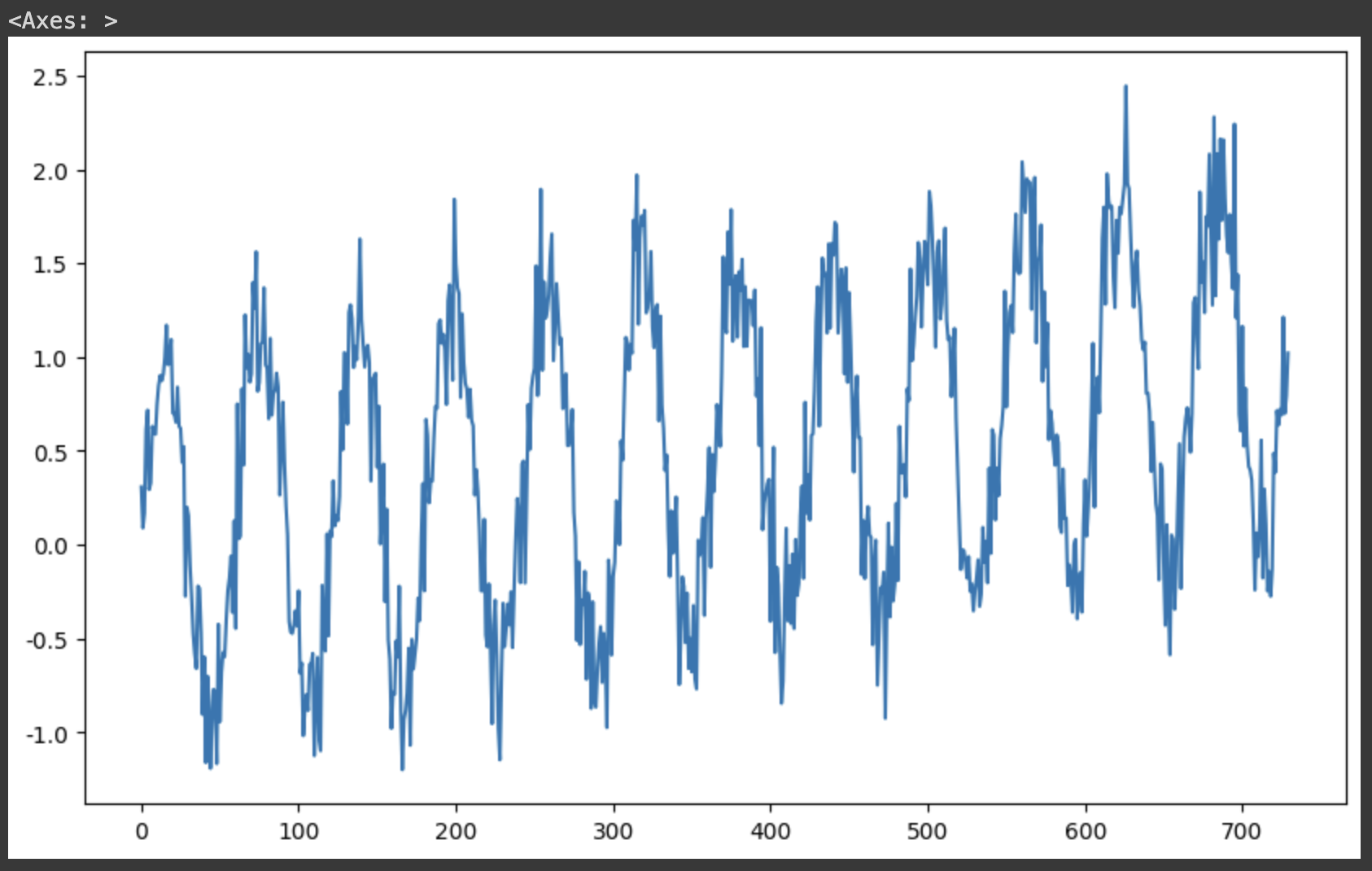

m = Prophet(yearly_seasonality=True, daily_seasonality=True)
m.fit(df)
future = m.make_future_dataframe(periods=30)
forecast = m.predict(future)
m.plot(forecast);

그다음 향후 30일을 예측하면 다음과 같이 나온다.

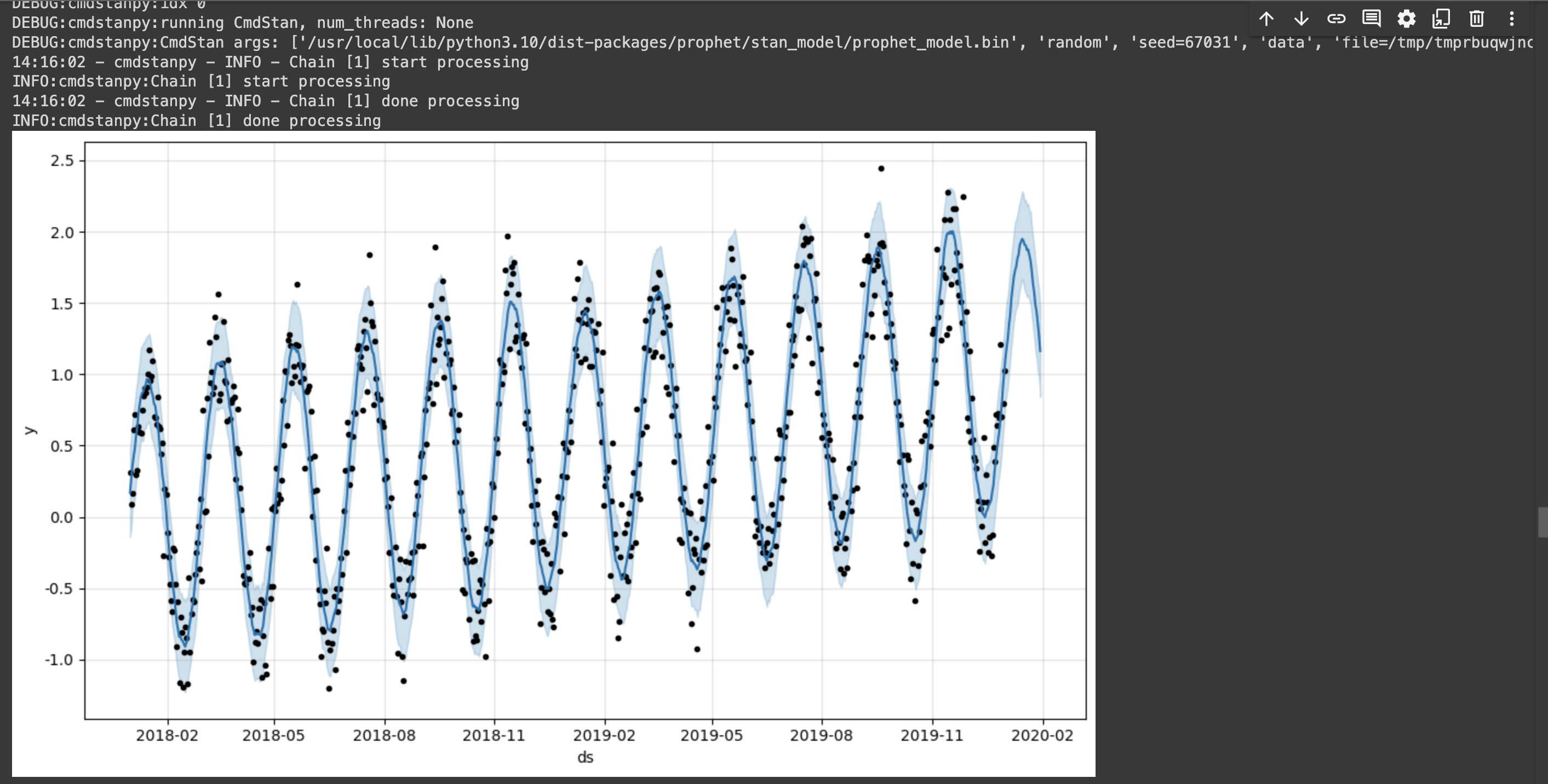
5. 시계열 데이터 실전 이용하기

먼저, numpy를 이용해서 trend파악은 해보자

import pandas as pd
import pandas_datareader as web
import numpy as np
import matplotlib.pyplot as plt

from prophet import Prophet
from datetime import datetime

%matplotlib inline

코랩으로 csv파일을 가져오려면 google drive에 마운트 해야하는데,
그 방법은 https://resultofeffort.tistory.com/60 여길 참고하길 바란다.

from google.colab import drive
drive.mount('/content/drive')
pinkwink_web = pd.read_csv(
    '/05_PinkWink_Web_Traffic.csv',
    encoding="utf-8",
    thousands=",",
    names=["date", "hit"],
    index_col=0
)

pinkwink_web = pinkwink_web[pinkwink_web["hit"].notnull()]
pinkwink_web.head()

hit에 null값이 있어서, null값이 없는 것만 나오도록, 위 코드를 작성해 준다.

pinkwink_web

1) 전체 데이터 그려보기

pinkwink_web["hit"].plot(figsize=(12, 4), grid=True);

전체 기간 중 방문자 수이다.

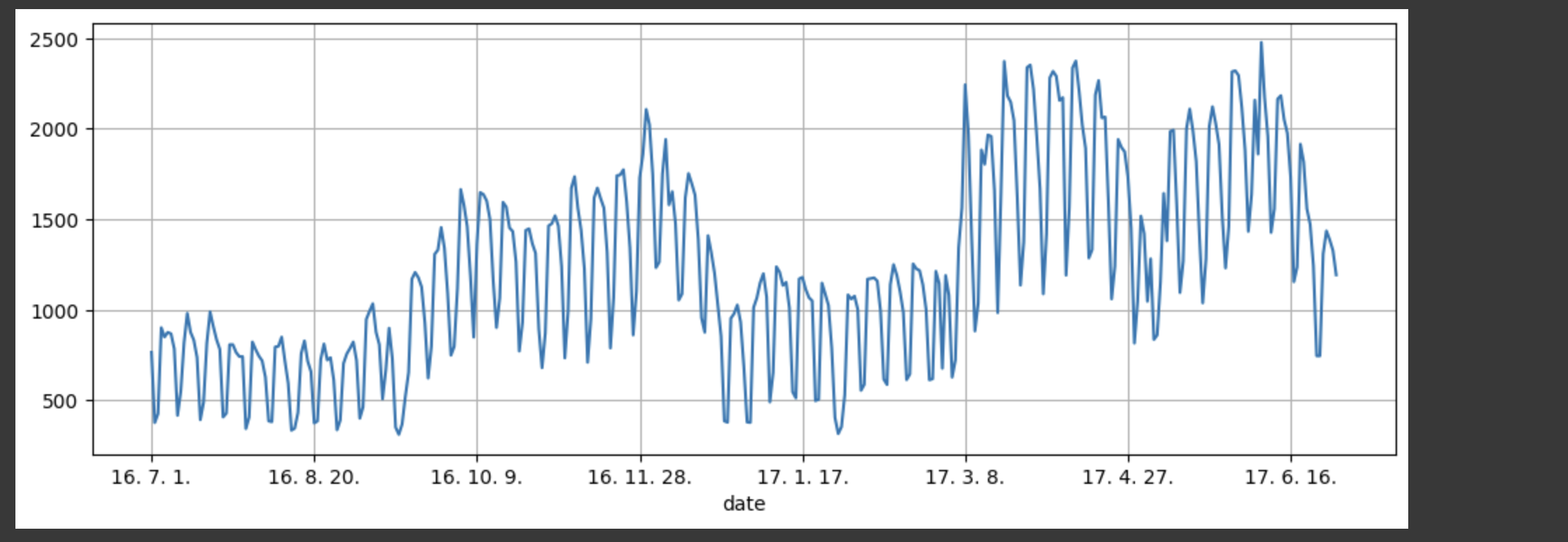
2) trend 분석을 시각화 하기 위한 x축 값 만들기

time = np.arange(0,len(pinkwink_web))
traffic = pinkwink_web["hit"].values
fx = np.linspace(0, time[-1], 1000)

데이터의 총길이를 가지고 0부터 그 길이만큼 time을 잡는다.
hit컬럼의 values값을 traffic이라는 변수에 지정한다.
fx 함수는 linspace(1차원 배열을 만드는 기능)로 time을 포함시키면 안되기 때문에 타임의 마지막 번까지를 1000등분을 해 fx에 저장한다는 의미이다.

3) 에러 계산할 함수

def error(f, x, y):
  return np.sqrt(np.mean((f(x) - y) ** 2))

트렌드를 만들어내고, 얼마나 원데이터를 잘 반영하는지 정량적 평가 지표를 '에러'라고 본다.
에러 함수는 x값을 받아들고 f함수를 받아들고 y는 참값
f(x)는 예측값 y는 참값. f(x) - y 이 차이가 에러이다.
에러의 제곱의 평균을 루트 씌우면 = RMSE라고 부른다.

* 평균 제곱근 오차(RMSE)는 회귀 예측 모델에 대한 두 개의 주요 성과 지표 중 하나이다.
평균 제곱근 오차는 예측 모델에서 예측한 값과 실제 값 사이의 평균 차이를 측정한다. 
예측 모델이 목표 값(정확도)을 얼마나 잘 예측할 수 있는지 추정한다.

시간과 트래픽을 가지고 1차함수, 2차함수, 3차함수, 15차 함수를 만들라 시킨다음에
ployfit을 통과시키면 계수가 나오고, 계수를 각각의 변수명을 가지고 poly1d를 통과시키면
f1, f2, f3, f15가 함수가 된다.

1차, 2차, 3차 함수까지는 에러의 큰 차이가 없다.
그런데 15차에서 크게 나타났다.
이런 경우, 3차식을 할 바에는 1차식으로 하거나, 아니면 15차식으로 하겠다고 선택할 수 있다.

fp1 = np.polyfit(time, traffic, 1)
f1 = np.poly1d(fp1)

f2p = np.polyfit(time, traffic, 2)
f2 = np.poly1d(f2p)

f3p = np.polyfit(time, traffic, 3)
f3 = np.poly1d(f3p)

f15p = np.polyfit(time, traffic, 15)
f15 = np.poly1d(f15p)
(error(f1, time, traffic))
print(error(f2, time, traffic))
print(error(f3, time, traffic))
print(error(f15, time, traffic))

plt.figure(figsize=(12, 4))
plt.scatter(time, traffic, s=10)
plt.plot(fx, f1(fx), lw=4, label='f1')
plt.plot(fx, f2(fx), lw=4, label='f2')
plt.plot(fx, f3(fx), lw=4, label='f3')
plt.plot(fx, f15(fx), lw=4, label='f15')

plt.grid(True, linestyle="-", color="0.75")
plt.legend(loc=2)
plt.show()

파란색 점이 원데이터이고, 빨간색이 15차식이다.
나라면 1차식으로 선택하겠다.

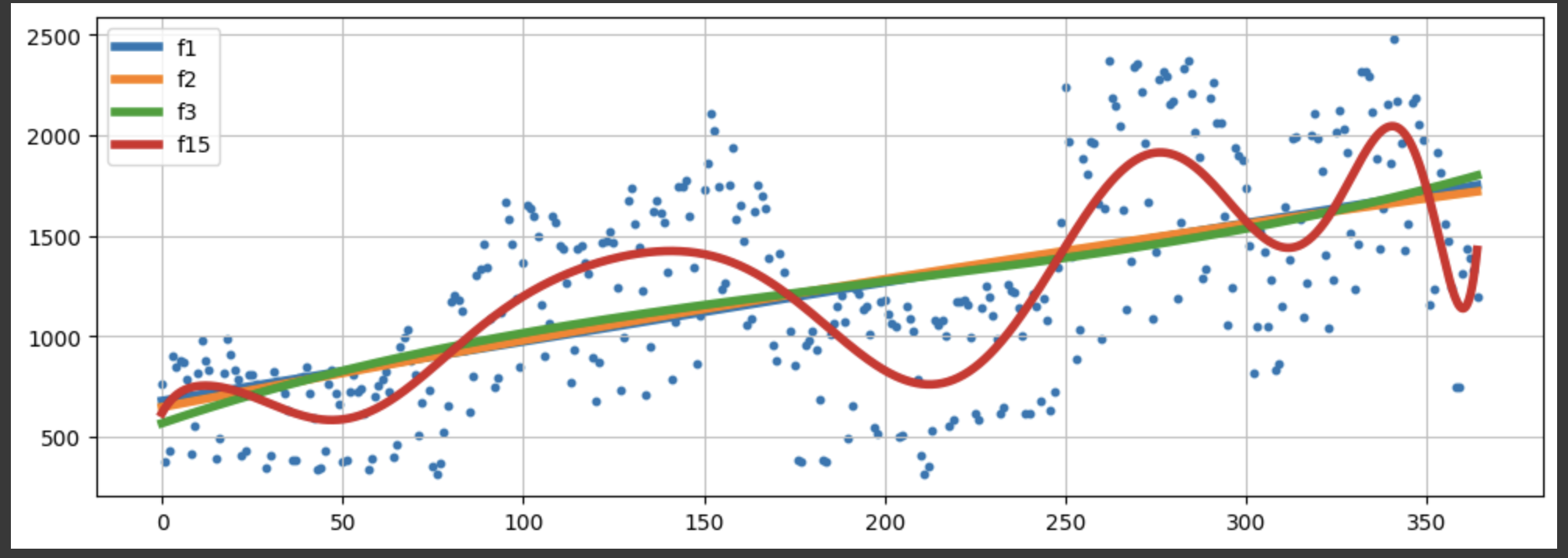
df = pd.DataFrame({"ds":pinkwink_web.index, "y":pinkwink_web["hit"]})
df.reset_index(inplace=True)
df["ds"] = pd.to_datetime(df["ds"], format="%y. %m. %d.")
del df["date"]
df.head()
  • ds: index
  • y: 방문자수
  • format(연도, 월, 일)

m = Prophet(yearly_seasonality=True, daily_seasonality=True)
m.fit(df);

4) 60일에 해당하는 데이터 예측

future = m.make_future_dataframe(periods=60)
future.tail()

5) 예측 결과는 상한/하한의 범위를 포함해서 얻어진다

ds: 날짜형 데이터

forecast = m.predict(future)
forecast[["ds", "yhat", "yhat_lower", "yhat_upper"]].tail()

m.plot(forecast);

60일 간의 데이터를 보니, 그럴싸하게 나오고 있다.
주기성이 좋을 수록 예측력이 좋아진다.

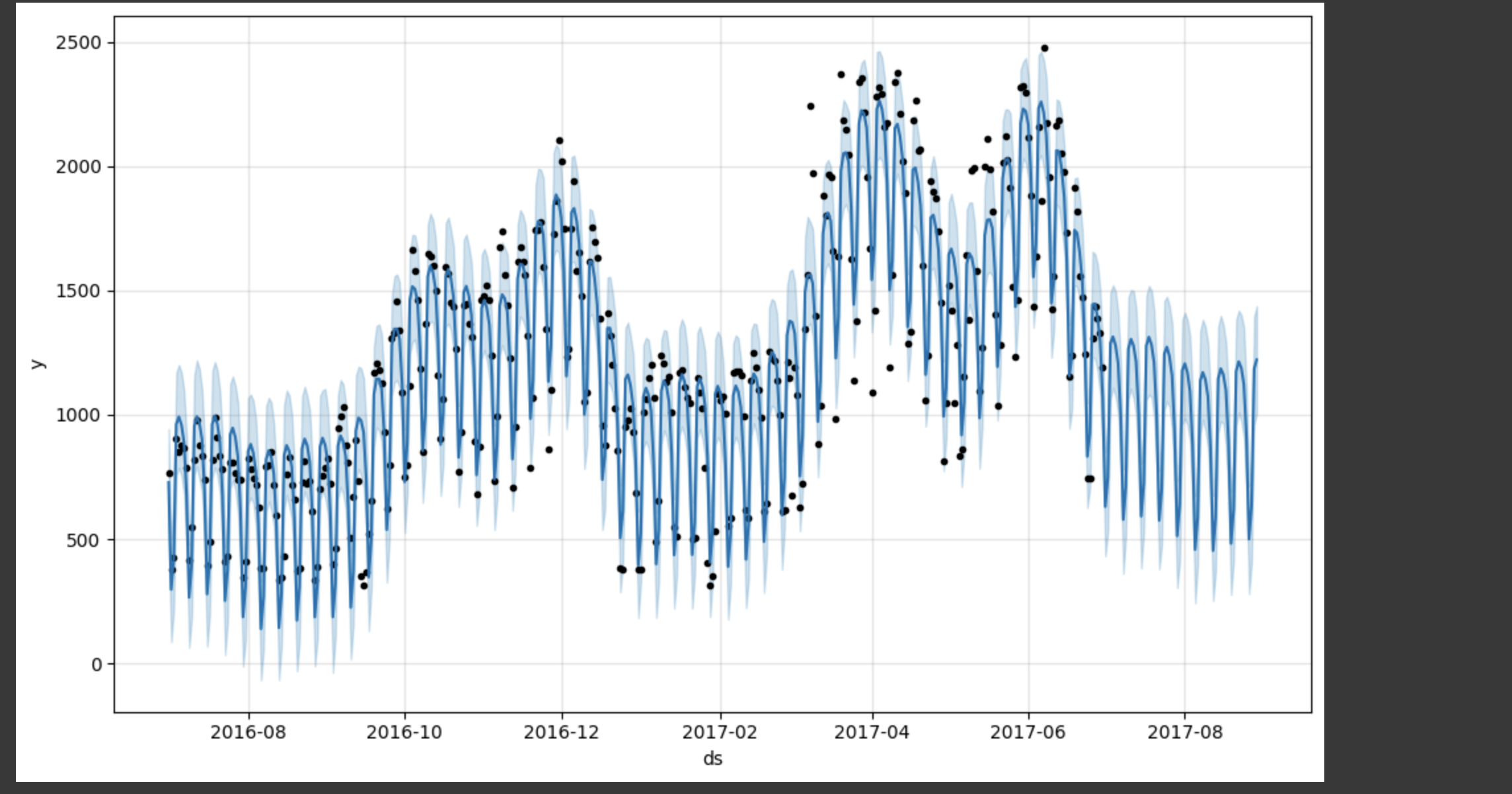
m.plot_components(forecast)

forecast 결과에 대해 component를 확인할 수 있다.

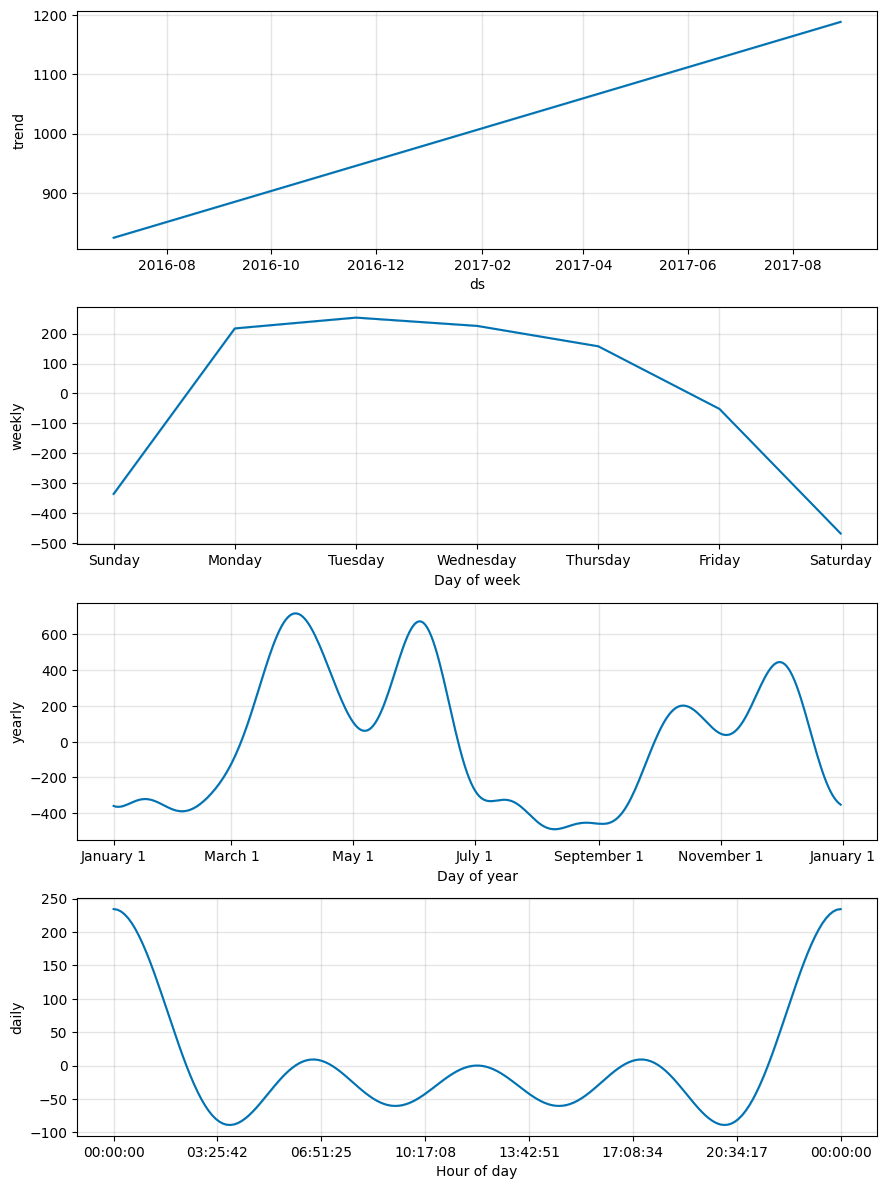
각 주제에 맞는 데이터 그래프도 그려볼 수 있다.

결과, 트렌드 대비 월요일, 화요일에 방문객 수가 많다.
연간 그래프를 보니, 3월~4월, 11월~12월에 방문수가 많다.

강의용으로 사용되었다는 것으로 보아 중간고사, 기말고사 기간에 방문수가 증가했구나 파악할 수 있다.

profile
전주미
data dreamer
이전 포스트

[시계열] 시계열 도표란?

다음 포스트

[Web Data] BeautifulSoup for web data

0개의 댓글