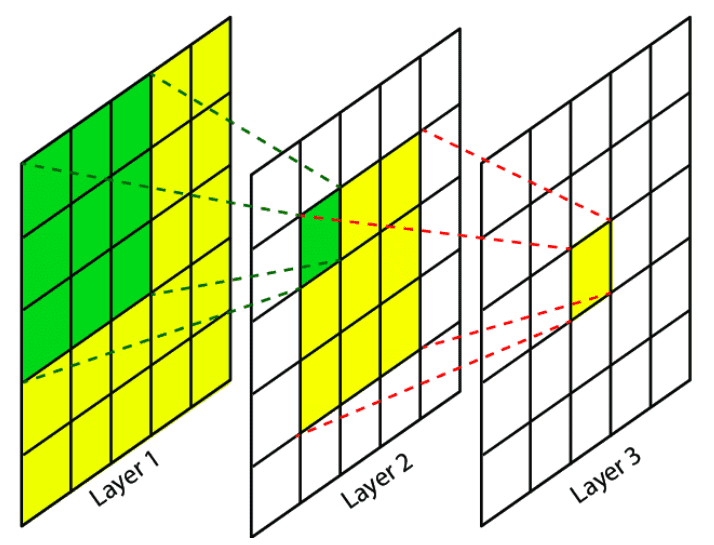
이제서야 Segmentation에 대한 논문 리뷰를 쓰는 것 같다. 특히, Segmentation에 대해 자세히 알기 위해선 아주 기본이 되는 Paper중에 하나이지 않을까? 인용이 20000회나 되는 대단한 Paper이다. Class를 분류하는 것에 그치지 않고 해당 Class가 어디에 있는지에 대한 정보도 제공한다. (FCL을 사용하지 않고 모든 layer을 Convolution으로 구성했다는 것이 흥미롭다.) 리뷰 순서는 Paper순으로 진행을 하며 FCN의 idea를 제대로 이해할 수 있도록 구성하였다.
FCN Paper : https://arxiv.org/pdf/1411.4038.pdf
Abstract
"We show that convolutional networks by themselves, trained end-to-end, pixels to-pixels, exceed the state-of-the-art in semantic segmentation. Our key insight is to build “fully convolutional” networks that take input of arbitrary size and produce correspondingly-sized output with efficient inference and learning. "
자신들이 만든 Convolution Network는 end to end 방식이며 기존의 Semantic segmentation 분야에 있어서 엄청난 성능을 보여준다고 한다. 모든 layer들이 Convolution layer로 구성되어 있어 어떤 임의의 input이 들어와도 그에 상응하는 output을 내보낼 수 있다고 한다. 이를 이해하기 위해선 다음을 알아야 한다.
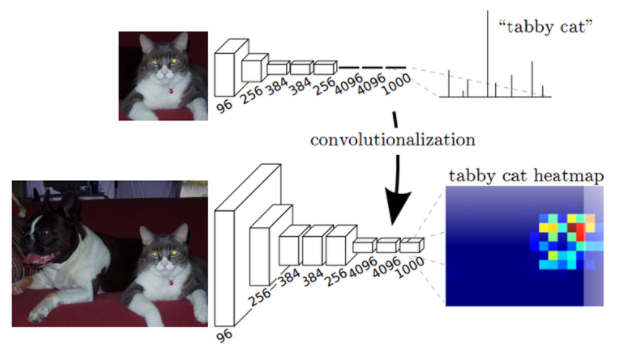위의 Network부터 살펴보자. 위의 Network는 Conv5까지 사용하고 그 뒤로는 FCL(Fully connected layer)을 사용한다. 이 FCL은 2가지의 한계점을 갖는다.
FCL의 한계점
1. 이미지의 위치 정보가 사라진다.
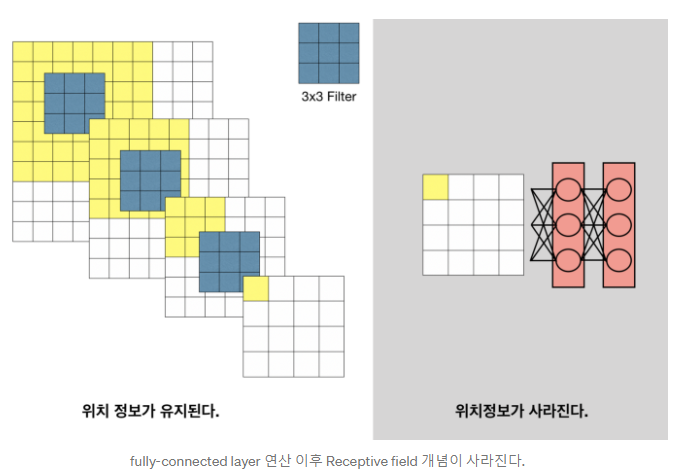Convolution과 Pooling을 사용하여 작은 feature map을 만들지라도 하나의 feature map은 어느 정도 spatial coordinates인 spatial에 대한 Location information을 갖는다. 그러나 이 Network의 last에 FCL을 사용하게 되면 Classification은 할 수 있으나 Location information은 모두 사라진다.
2. 입력 이미지가 고정된다.
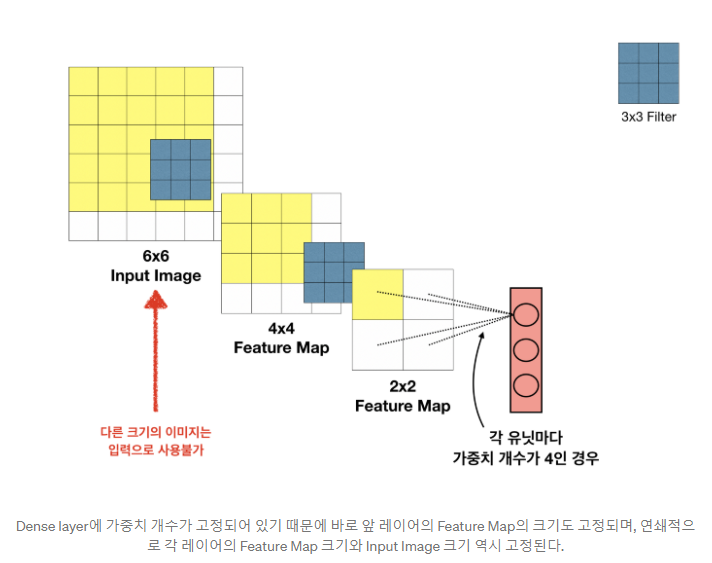FCL을 사용하기 위해선 feature map이 고정되어야 한다. weight의 갯수가 고정되어 있기 때문에, 그 이상의 weight가 들어오게 되면 사용할 수가 없다. 그림을 보면 연쇄작용으로 인해 그 전 layer의 feature map도 계속해서 고정된 것을 볼 수 있다. 이렇게 되면 input image는 무조건 6 x 6 이어야 한다.
Paper의 Abstract에서는 이런 FCL의 한계를 해결하기 위해서, 모든 layer에 Convolution을 적용하여 input of arbitrary size가 가능하다고 언급하고 있다.
또 paper에서 자주 사용하는 용어들이 있는데, 짚고 넘어가도록 하자. 바로 Coarse 와 Fine이다.
Coarse : 거친
fine : 미세한, 조밀한
이를 이해하기 위해서 어디서 이런 단어를 사용하는지 알아보자.
느낌이 오려나 모르겠다. 쉽게 말해서, Coarse는 큼직 큼직하게 분류하는 느낌이 강하다. 비행기의 종류가 달라도 비행기로 인식하는 것처럼 말이다. Fine 같은 경우에는 강아지 Class에서 어떤 강아지인지 분류하는 느낌이 강하다. 강아지의 종류에도 리트리버, 진돗개, 불독 등등 다양하지 않은가?
- Coarse는 대충 이게 무슨 class인지 확인하는 과정
- Fine은 어떤 Class인지 알고난 후 어떤 instance가 존재하는지에 대해 상세하게 확인하는 과정
1. Introduction
"To our knowledge, this is the first work to train FCNs end-to-end (1) for pixelwise prediction and (2) from supervised pre-training."
여기서 기존의 segmentation과의 차별점이 나온다. 기존의 segmentation같은 경우에는 patchwise 방법을 사용하였다.
Patch란?
: 하나의 이미지에서 object는 그대로 두고 background를 제거한 것을 patch라 한다.
텍스트
patchwise 방법이란?
: Patchwise training을 사용하는 이유는 이미지에 필요없는 정보들이 존재할 수 있고, 하나의 이미지에서 서로 다른 object가 존재하는 경우 redundancy(중복성)가 발생한다. 즉, Object와 관련된 feature을 추출해야 하는데 필요없는 배경까지 본다면 불필요한 computation(계산)이 발생한다.
하지만 Patchwise 방법도 엄청난 computation이 발생하기 때문에, 좋지 않다. FCN에서는 Patchwise 방법을 사용하지 않는다 라고 언급한다.
한번에 전체 이미지를 feedforward computation과 backpropagation을 사용하여 learning 과 inference를 한다고 한다. 또한 FCL을 사용하지 않고 Fully convolution을 사용하여 upsampling 과정을 거치는데, 이때 subsampling pooling을 사용하여 pixelwise(픽셀별) prediction과 learning이 가능하다고 한다. (이 부분에 대해 이해하지 못해도 상관없다. 뒤의 본론 내용에서 더 자세하게 설명하도록 하겠다.)
또한, 새로운 "skip architecture"을 구성하여 deep, coarse, semantic information and shallow, fine, appearance information을 결합할 수 있다고 한다. (이는 뒤의 semantic segmentation 부분을 설명하면서 상세하게 설명하도록 하겠다.)
2. Fully Convolutional networks
"Locations in higher layers correspond to the locations in the image they are path-connected to, which are called their receptive fields."
Fully convolutional network에 대해 알기 위해선 우선 receptive fields에 대해 알아야 한다.
receptive field (수용 필드)
: 상위 layer의 location은 경로가 연결된 이미지의 위치에 해당하며 이를 receptive field라 한다.
즉, 쉽게 말하면 receptive field = filter size 라고 볼 수도 있다.
receptive field에 대해 말한 이유는 patchwise 때문이다. 앞서 말했듯이 FCN 저자들은 patchwise 방법을 사용하지 않는다고 하였다. 그 이유는 computation 문제이기 때문이다.
"When these receptive fields overlap significantly, both feedforward computation and backpropagation are much more efficient when computed layer-by-layer over an entire image instead of independently patch-by-patch."
저자들은 patchwise보다 receptive fields가 크게 겹치면 feedforward computation과 backpropagation을 사용하는 것이 computation performance가 뛰어나다고 말하고 있다.
2.1 Shift and stitch is filter rarefaction
FCN은 이 방법을 사용하지 않는다. 이 방법에 대해 자세히 알고 싶다면 여기를 참고하라.
https://stackoverflow.com/questions/40690951/how-does-shift-and-stitch-in-a-fully-convolutional-network-work
사용하지 않는 이유는 계산 비용이 매우 크기 때문이다. 기존의 shift and stitch 알고리즘은 max_pooling을 사용한다. 하지만 기존의 방법보다 'skip architecture'의 performance가 훨씬 뛰어나기 때문에 사용하지 않는다.
2.2 Upsampling is backwards strided convolution
FCN 저자들은 interpolation(보간법)을 사용한다. 그중에서도 bilinear interpolation을 사용한다고 한다. (참고 :https://medium.com/@msmapark2/fcn-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0-fully-convolutional-networks-for-semantic-segmentation-81f016d76204)
interpolation(보간법)
우선 Linear interpolation에 대해 먼저 알아보자.
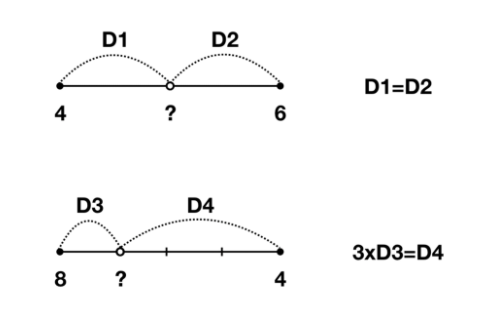위의 값은 5이고 아래의 값은 7임을 직관적으로 알 수 있다. 하지만 이를 구할 때도 식이 존재하는데 아래의 그림을 보자.
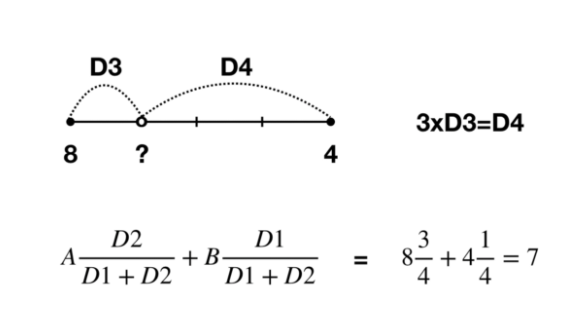그림을 보고 수식을 보면 이해가 될 것이다. (D1 == D3, D2 == D4)
Bilinear interpolation은 Linear interpolation을 확장한 것 뿐이다.
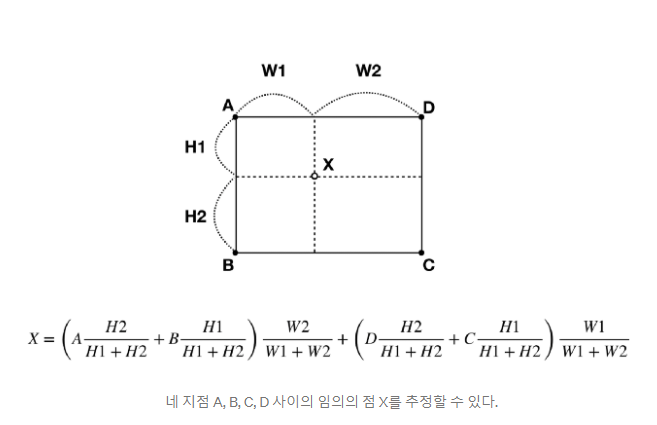이러한 방법을 사용한다면 우린 작은 feature map에서 더 큰 feature map을 만들 수 있다.
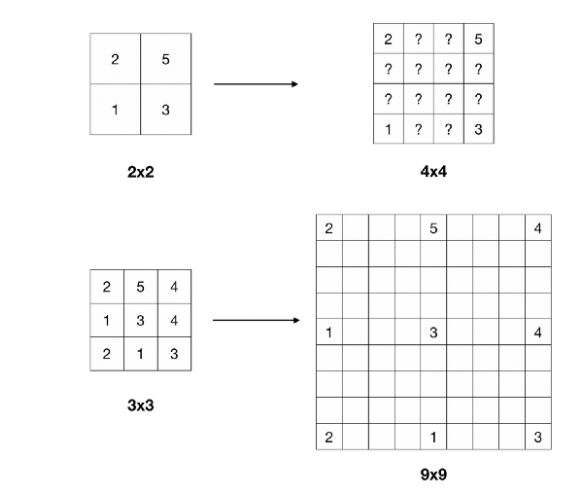
Backwards Convolution (Deconvolution)
또한 여기에 Backwards Convolution 개념도 사용되는데, 이를 deconvolution이라 부르기도 한다. 즉, 말 그대로 convolution을 역으로 사용한다는 뜻이다.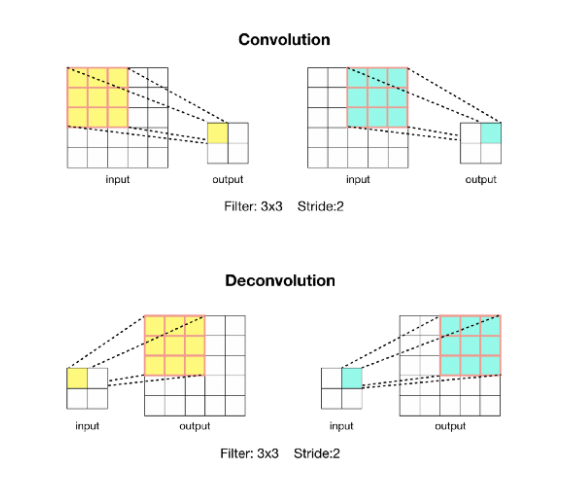 
우리가 보통 convolution을 하면 down sampling하는 효과를 내어 output인 feature map이 점점 작아지는 현상이 보인다. 하지만 이를 반대로 하는 Deconvolution을 사용하면 upsampling이 되어 output인 feature map이 점점 커진다. FCN에서는 아래의 그림과 같은 방법으로 동작한다. 
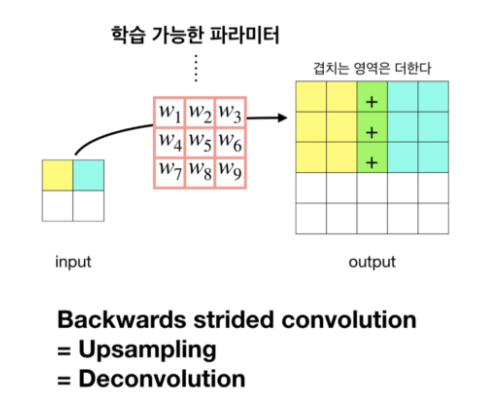즉, FCN에서는 Bilinear interpolation과 Backwards convolution 두 가지 방법을 사용하여 Coarse Feature map으로 부터 Dense Prediction을 구한다.
하지만 이와 같은 방법을 사용해도 input image처럼 upsampling하기에는 문제가 많다. 그 이유는 이미 down-sampling을 사용하여 feature map의 size가 매우 작아져 있는 상태이기 때문이다. 그림으로 보여준다면,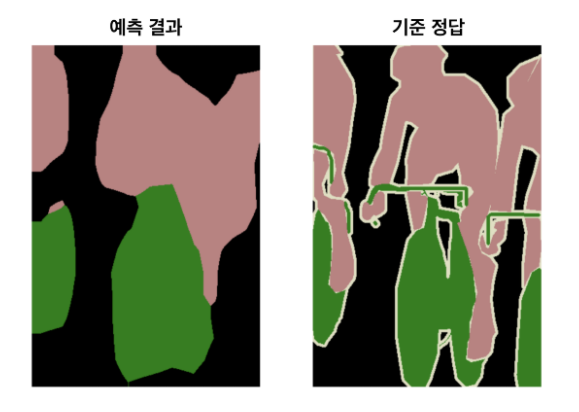 
이러한 문제가 발생한다. interpolation과 backwards convolution만으로는 한계가 있다는 것이 명확해졌다.
2.3 Patchwise training is loss sampling
앞서 말했듯이 FCN에서는 Patchwise를 사용하지 않는다. 따라서 paper에 나온 부분을 요약하여 넘어가도록 하겠다.
- Patchwise : class의 불균형을 수정하고 조밀한 patches들의 공간적 상관관계를 완화할 수 있다.
- Fully Convolutional training : Class 균혀은 loss에 weight를 부여하여 얻게 되며, loss sampling을 사용하여 공간 상관 관계를 해결함.
논문에서는 Fully Convolutional training이 computation performance가 더 뛰어나다고 말한다.
3. Segmentation Architecture
"we build a novel skip architecture that combines coarse, semantic and local, appearance information to refine prediction." 이 절의 keypoint이다.
저자들이 새로 만든 "Skip Architecture"란 도대체 무엇일까? 이것이 interpolation과 backwards convolution의 한계도 해결한 것인데, 도대체 무슨 방법일까?
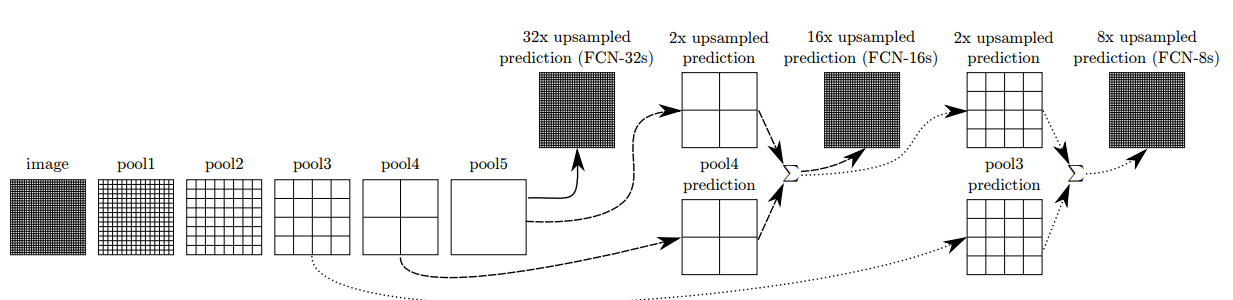
위의 (FCN-32s),(FCN-16s),(FCN-8s) process를 통해 output이 어떤식으로 만들어지는지 확인해보자.
또 이를 직관적으로 표현하면 다음과 같다.
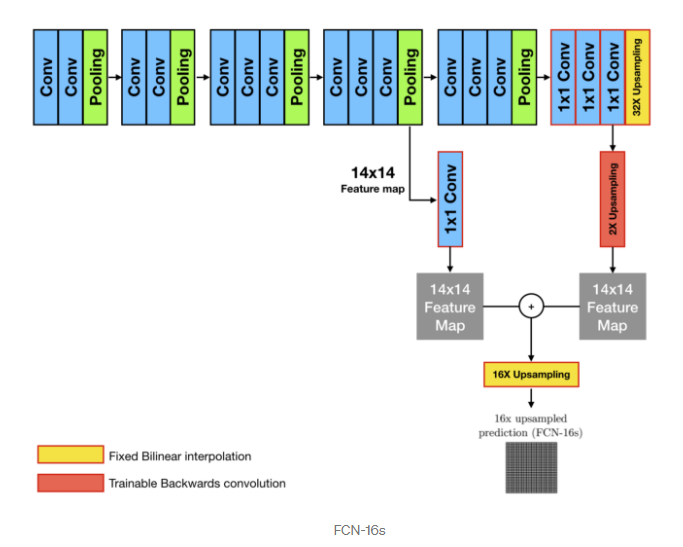
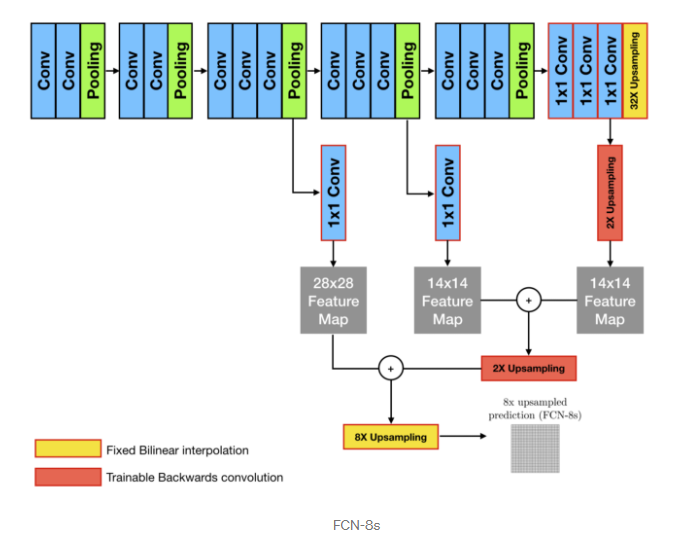
위의 과정을 통해 Semantic Segmentation이 이뤄지는 것을 볼 수 있다.
실제 성능 지표를 확인해보면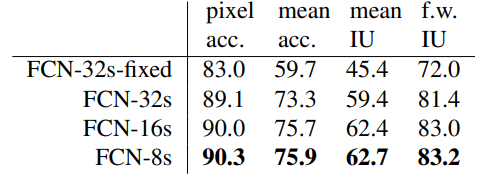 
점점 증가하는 것을 알 수 있다. 여기서 IU는 interaction over union의 약어인데, 이에 대해 모른다면 https://velog.io/@joon10266/Objection-Detection-mAP%EB%9E%80 참고하자!
Summary
FCN은 기존의 Semantic segmentation에서 수정하여 transfer learning을 하였다. 또한, End-to-End 방식이 가능하고 나중에 나오는 U-net, Mask R-CNN등에 reference로 달려있다.
Fully connected layer을 convolutionalize하여 공간 정보를 갖고 가는 방법을 사용하였다.
또한, shallow층의 local information 정보와 deep층의 global information을 combine하는 skip connection을 사용하여 보다 정교한 semantic 결과를 얻을 수 있다.
