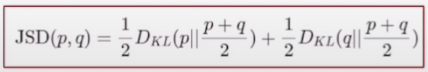요즘 Object Detection 관련으로 영상관련 공부를 계속하고 있다. YOLO 논문 리뷰를 끝내고 다른 1-stage, 2-stage 방식의 논문을 읽고 리뷰를 남기려고 했으나, 문득 아이디어가 떠올랐다. 4학년 졸업작품을 만들면서 length image data를 모아둔 적이 있다. 이 length image data size가 160*90인데, 이를 stylegan을 사용하여 고화질로 만들어 보고 싶었던 것이다. super-resolution의 기법을 써서 저화질을 고화질로 만들고 싶은건데, 그러기 위해선 그 기반이 되는 GAN에 대해 어느 정도의 concept는 알고 있어야 도움이 될거라 생각하여 분석해보았다.
GAN은 Generative Adversarial Nets로 생성적 적대 신경망이라 불린다. 생성적 적대 신경망(?)이건 무엇일까? 생성도 하는데 적대도 한다니... 무슨말인지 알아보자.
구성은 GAN의 paper 순으로 작성을 하도록 하겠다.
들어가기 앞서, GAN 을 "간"이라 부르는 사람도 있고, "갠"이라고 부르는 사람도 있다.
GAN paper : https://arxiv.org/pdf/1406.2661.pdf
1. Abstract
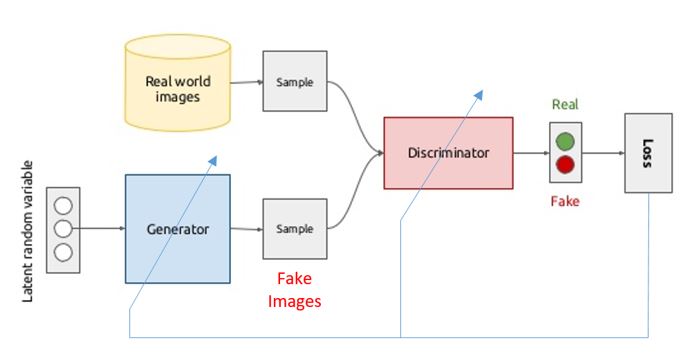
GAN은 두개의 model로 구성되어 있으며 adversarial process를 통해 generative model을 estimate한다. (즉, adversarial Net를 통해 지속적인 feedback을 받는다.)
Paper에서 generative model을 G라 표현하고 discrimiative model을 D라 표현한다. (이번 리뷰에서 G, D로 사용할 예정이니 알아두셔야 합니다!)
generative model(G) : captures the data distribution
discriminative model(D) : estimates the probability that a sample came from the data
'capture'의 단어 뜻은 '잡다', '포획하다'라는 뜻을 갖는다. 그렇다면 '데이터의 분포를 잡는다'라는 것이다. 간단하게 말하자면, G는 training data의 데이터의 분포를 잡기위해 노력하고 학습한다. D는 G로부터 학습하는 것이 아닌 training data의 sampling값에 대한 확률을 측정한다.
paper에선 이들을 minmax game이라 간주한다. G는 D가 자신이 만든 'Fake data'를 통과시킬수 있도록 최대한 실수를 유발시킨다. 즉, G가 만든 'Fake'data를 D가 이것이 'Fake'인지 'real'인지 구분할 수 없도록 하는데, 확률로 따지자면 (1/2 = 0.5)을 갖도록 하는 것이다.
"갑자기 뜬끔없이 웬 콜라지?"라고 생각할 것이다. 맛 혹은 탄산에 대해 민감하지 않은 사람인 경우에는 코카콜라와 펩시를 구분하지 못한다고 한다. 이런 사람들에게 눈을 가리고 오직 맛으로만 무엇인지 맞추라고 하면 그들은 1/2확률로 찍을 수 밖에 없는 것이다. 하지만 이마트, 홈플러스에서 만든 콜라는 맛이 달라서 민감하지 않은 사람들도 얼추 맞춘다고 한다.
내가 말하고 싶은 요지는 여기서 나온다. train data가 코카콜라, D를 맛에 민감하지 않은 사람이라 가정하자. 여기서 GAN을 사용하여 학습한다고 생각하자. 몇번 학습을 하며 G는 D의 꾸준한 feedback을 받으며 'fake'를 양산한다. 그때 G의 data를 확인해보니 이마트, 홈플러스 콜라를 만들어냈다. 이는 D가 'fake'라고 판단할 확률이 높다. 하지만 이를 여러번 반복 수행하게 되면 결국에, G는 펩시와 같은 콜라를 양산하게 된다. 이때, D는 이것이 'Fake'인 펩시인지 'real'인 코카콜라인지 구별할 수 없게 된다.
G와 D는 multilayer perceptron으로 구성되며 backpropagation을 통해 학습을 진행한다.
2. Introduction
"Deep generative models have had less of an impact, due to the difficulty of approximating many intractable probabilistic computations that arise in maximum likelihood estimation and related strategies, and due to difficulty of leveraging the benefits of piecewise linear units in the generative context."
기존의 generative model은 두가지의 한계점이 존재했다.
-
difficulty of approximating many intractable probabilistic computations
확률적 계산에 대한 근사화의 어려움을 격는다. 이 근사화의 어려움이란 unsupervised learning중에 하나여서 그렇지 않을까 생각한다. target이 없는 상태에서 무언가에 근사하기엔 엄청난 도전이다. 즉, adversarial Net이 없어서 기존의 generative model은 어려움을 겪지 않았을까.. -
difficulty of leveraging the benefits
generative context의 무언가에서 활용하기 까다로웠다고 한다. 이 내용은 기존의 generative model에 대한 지식이 있어야 설명할 수 있을 것 같다.
본격적으로 GAN에 대한 Architecture을 확인해보자.
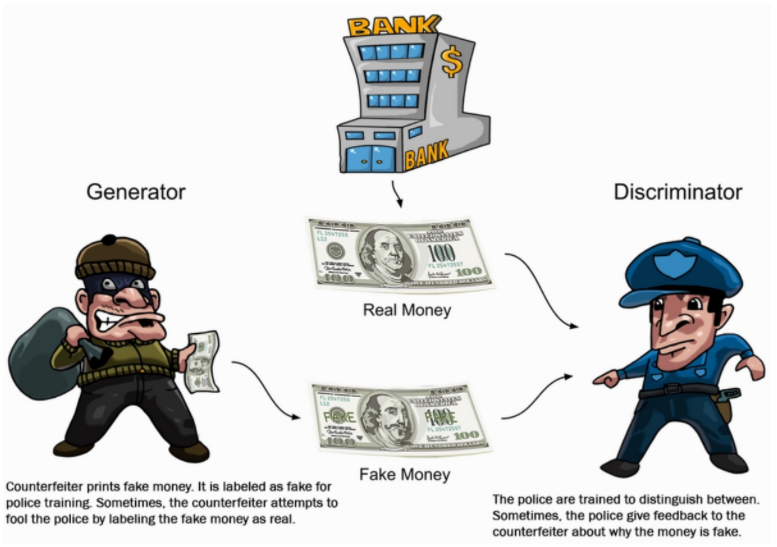(그림은 https://velog.io/@sanha9999/%EB%85%BC%EB%AC%B8%EC%9D%BD%EA%B8%B0-GAN 여기서 가져왔습니다.)
paper에서도 그림과 같이 설명한다. counterfeit team(위조팀)이 Fake currency(위조 화폐)를 만들고 police는 그게 Fake currency 인 것인지, 진짜 real currency인지 확인한다. police가 fake인 것을 감지하면 counterfeit는 그 feedback을 통해 가짜인지 진짜인지 모를 정도의 currency를 만들어 나간다.
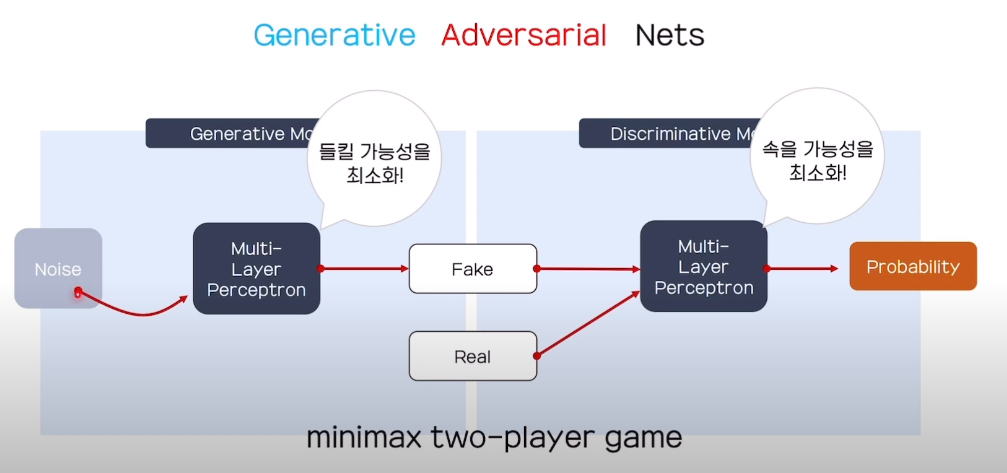이것이 GAN의 Architecture이다.
2. Related work
GAN에 대한 paper을 읽어나가는데 이 부분은 크게 영향을 미치지 않아 짧게 설명하고 마치겠다.
기존의 볼츠만 머신 같은 경우에는 likelihood gradient에 많은 근사치를 적용한다. 이를 통해 generative model을 구현하였는데, GAN같은 경우에는 근사치가 아닌 backpropagation을 통해 학습시킨다는 것이다.
3. Adversarial nets
여기서부터 정말 많은 수식이 나오게 되는데, 집중하며 하나씩 알아가보자.
본격적으로 들어가기 전에, GAN은 generator와 discriminator 중에 하나를 고정하고 남은 나머지를 학습한다. 이를 알아야 다음에 나오는 수식에 대해 쉽게 이해를 할 수 있다.
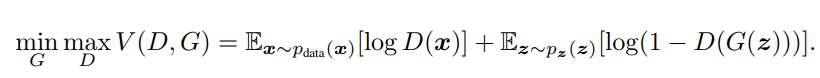"G는 V를 Minimize하며, D는 V를 Maximize한다."
자 우선, generator 부터 시작하자. 앞서 말했듯이 generator을 학습하기 위해선 discriminator는 고정되어야 한다.
G의 관점
G가 들어있는 항은 두번째 항만 보면된다. 첫번째 항은 상수로 취급되니 말이다. (이해 안되면 paper 4 page의 수식을 보면 된다.)
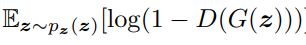GAN에서 G는 위의 수식 값을 Minimize 시켜야 한다.
즉 D(G(z))가 1에 가까워지면 가까워질수록 전체 수식 값은 Minimize된다. (여기서 D(x) = 1에 가까워지면 'real'로 판단하는 것이고, D(x) = 0 에 가까워지면 'fake'로 판단하는 것이다.)
D의 관점
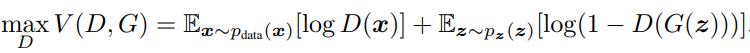GAN에서 D는 위의 수식 값을 Maximize시켜야 한다.
우선 첫 항부터 보게 되면 logD(x)를 보자. D(x)가 가질 수 있는 것이 D ~ 1까지 라는 것이다. 즉 1을 갖게 되야 제일 큰 값을 갖는 logD(x)가 나온다.
두 번째 항을 보자. log(1 - D(G(z)))가 maximize가 되려면 D(G(z))는 0에 수렴해야 한다. 그 이유는 D의 역할은 판별자 이므로 "Fake는 Fake다" 라는 것을 확실히 하기 위해서 위의 수식에 따라야 한다.
non-parametric limit
이 부분이 살짝 애매하다. 내가 제대로 이해한 것인지 말이다. non-parametric limit은 한국말로 비모수라는 것인데, target이 없는 상태인 unsupervised learning의 상황이 아닐까 싶다. (틀렸다면 댓글로 알려주세요.. 능력자들을 기다립니다.)
non-parametric : 모수에 대한 가정을 전제로 하지 않고 모집단의 형태에 관계없이 주어진 데이터에서 직접 확률을 계산하여 통계학적 검정을 하는 분석법
즉 Adversarial Net을 통해서 non-parametric limit 상황속에서도 data generator distribution을 구성(복구, 따라잡는)하는 지표를 이론적으로 보여준다.
위에서 말했듯이 G와 D는 둘 중에 하나는 고정하여 학습한 후, 그 순서를 뒤바꿔가며 학습을 진행한다고 했다. paper에서는 D같은 경우 k단계씩 optimize하며,G같은 경우는 한단계씩 optimize하는 식으로 진행했다고 한다. (이 부분은 나중에 code review를 통해 설명하도록 하겠다.)
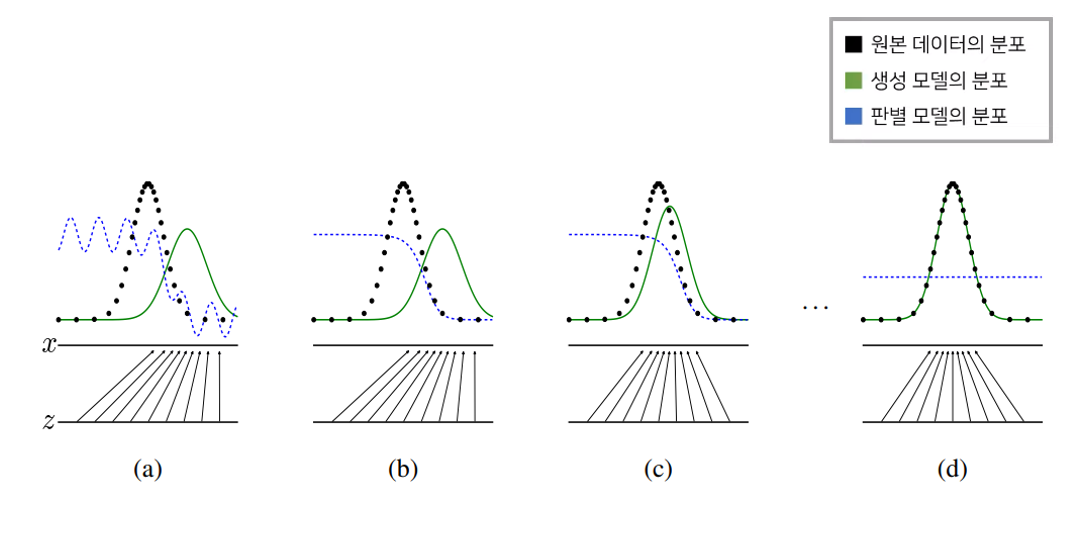과정을 한번 살펴보자.
(a) Intent vector들이 generator을 통해 sampling을 한 값 z가 training data에서 sampling된 값 x에 mapping되는 상황이다. 아까도 말했듯이 generator 만 학습시킨 과정인지라 discriminator의 확률 분포가 제대로 이뤄지지 않은 상황이다.
(b) discriminator을 학습하는 단계이다. 그렇다면 generator 부분은 학습하지 않아야 한다. (a) 단계에서 "Fake data"임에도 discriminator의 확률 분포가 날뛰는 현상이 발생하는데, discriminator을 학습하다보니 discriminator의 확률 분포가 제대로 이뤄지는 과정을 볼 수 있다.
(c) 또 다시 입장을 바꾸어 feedback을 받은 generator가 "real data"에 가까운 "fake data"를 내뱉고 그것의 확률 분포를 그래프로 나타낸 과정이다.
(d) 이 과정은 generator와 discriminator가 더 이상 학습할 필요가 없는 과정이다. 따라서 discriminator의 확률 분포가 1 / 2로 이루어진 것을 알 수 있다.
이를 직관적인 그림을 통해 제대로 이해해보자. (이 과정은 산업경영공학부 DSBA 연구실의 리뷰를 보고 참고하였습니다.)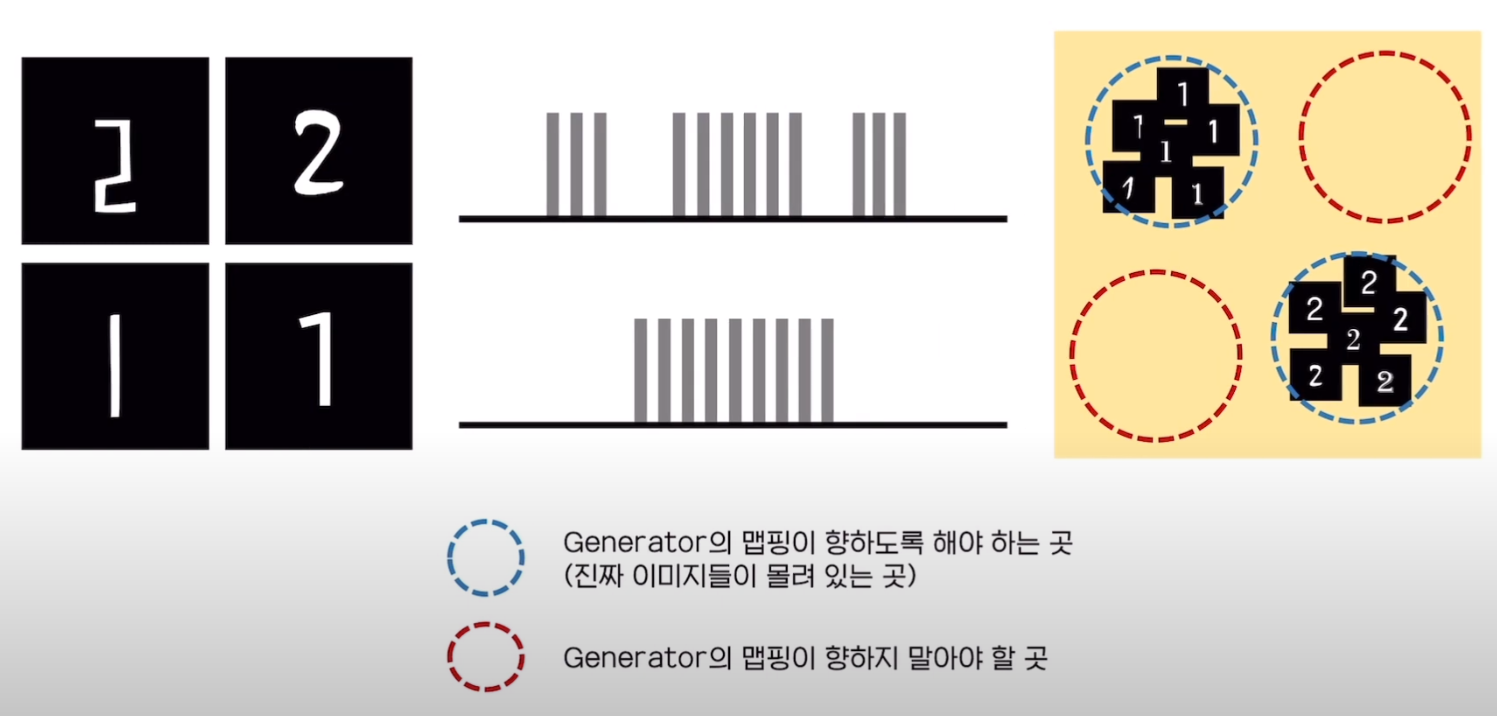
horizontal line 2개를 보자. 위의 line같은 경우에는 '2'에 대한 확률 분포를 나타낸 것이고, 아래의 line같은 경우에는 '1'에 대한 확률 분포를 나타낸 것이다.
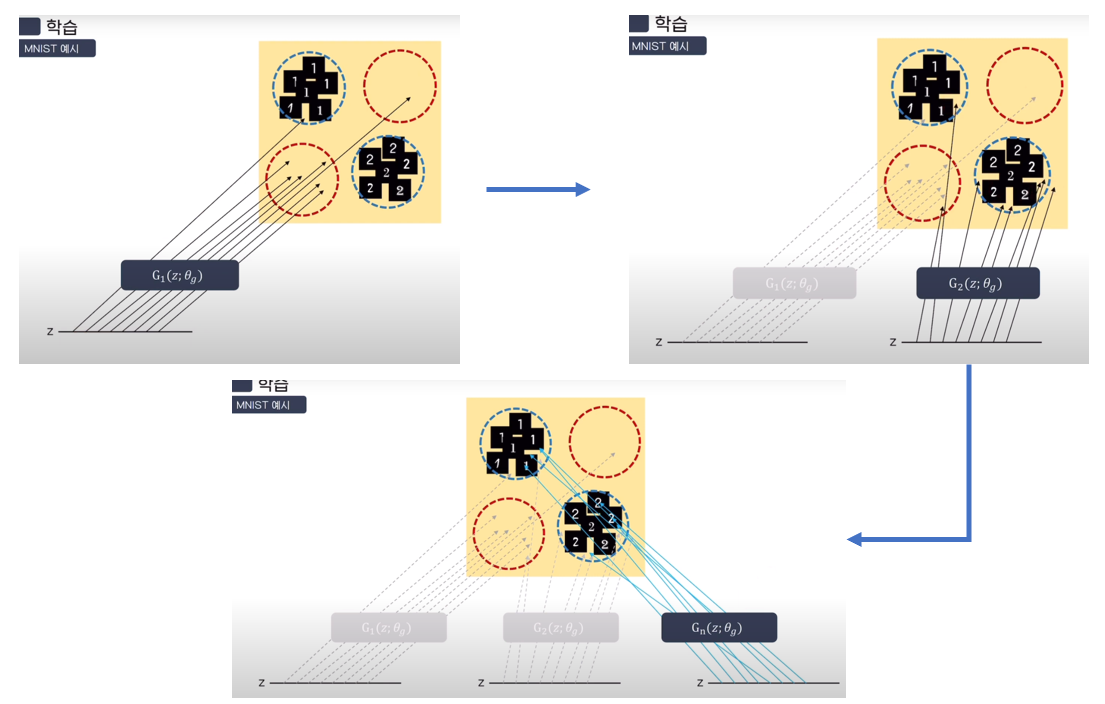학습 과정은 다음과 같다. 그림에서 표현된 G(z; θg)는 latent vector들이 옹기종기 모여있는 하나의 data space라고 생각하면 된다. 이들이 처음에 학습이 덜 되었을 때에는 mapping 되면 안되는 곳으로 가다가 학습을 진행하면 할수록 generator의 mapping이 training data sampling 값에 제대로 mapping이 되는 과정을 직관적으로 볼 수 있어 가져왔다.
4. Theoretical Results
이 부분은 완전 수학이다. 즉, 이 모델에서 이런 수식을 사용하여 증명을 했다는 것을 보여주기 위한 부분이다.
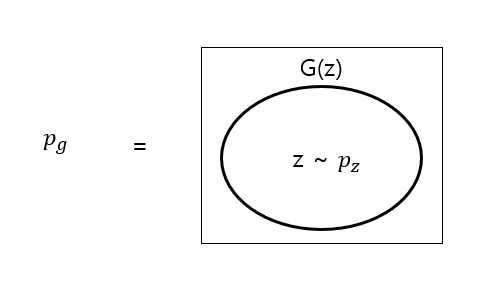위에서 한번 언급하긴 했었는데, 위의 4개의 graph 그림에서 초록색 선이 나타내는 것이 Pg이다. 이는 generator의 확률 분포로써 위의 그림처럼 생각하면 쉽지 않을까 하여 만들어보았다.
discriminator와 generator이 optimize를 하기 위해선 feedback 해줘야 하는데, 이를 담당하는 부분이다. 자세히 보면 앞의 objective function과 다를게 없는데, 거기에 미분이 들어간 것 뿐이다. (어려운 건 없음. 앞의 objective function이해하면 끝남.)
이해 못한 부분!
다만 여기서 아직 해결못한 부분이 있다. generator 부분을 살펴보자.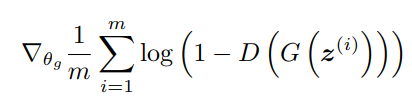
이는 descending gradient를 통해 generator에게 feedback을 update해주는 것인데, '-'의 유무가 궁금하다. 제대로 이해 못한 것일 수도 있는데, 알려주세요 궁금합니다...
좀더 찾아보면 -를 붙인 learning rate를 곱하여 update한다고 한다. 하지만 실제로 코드를 살펴보면 GAN에서 알려주는 lr = 0.0002 에 해당하는 hyperparameter을 넣는데, 이는 양수값이다. 뭔가 이상하지 않은가? 그래서 생각한 것이 "저기서 나오는 값은 음수로만 이루어져 있으니 -를 붙이지 않아도 descending gradient가 성립되는 것이 아닐까?" 라고 생각하고 있다.(아시는 분 알려주세요..)
해결했습니다! 아래의 그림을 참고해주세요!
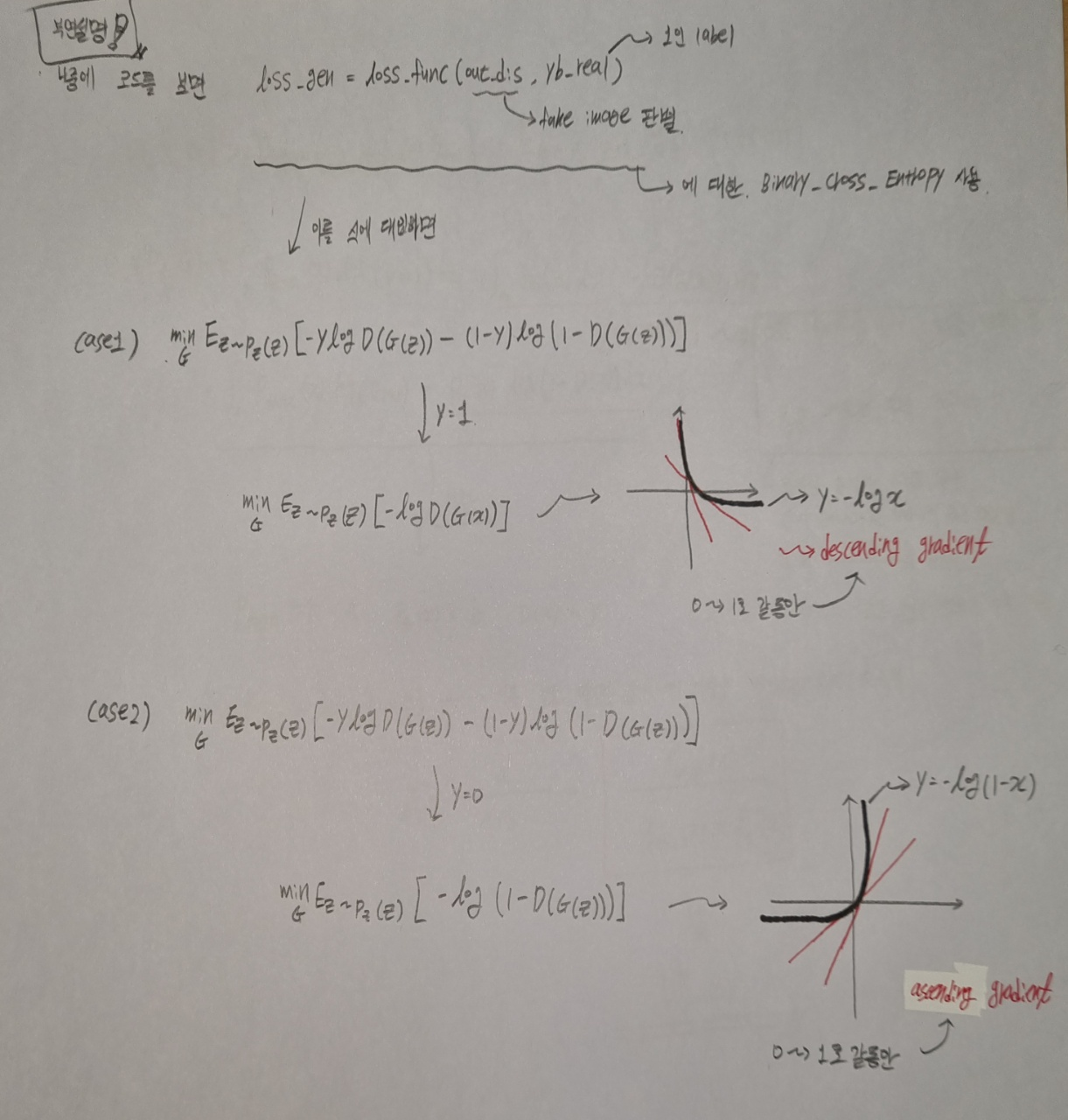
Proposition 1 (Global Optimality of Pg = Pdata)
이 부분에 대한 설명을 아래의 풀이 그림으로 대체한다.
Theorem 1
이 부분 같은 경우에는 Pg = Pdata 라면 C(G)는 -log4라는 것을 말한다. 그것을 증명한 것이다.
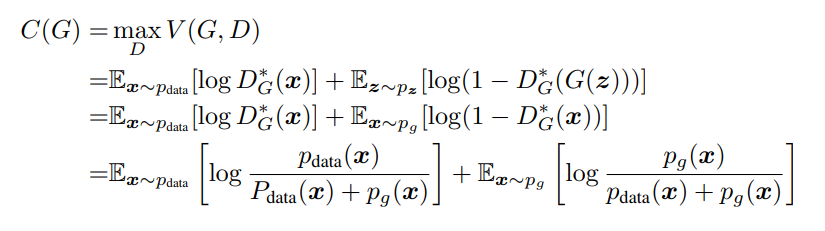기존의 objective function에서 위에서 구한 D*(x) 식으로 바꾼 것 뿐이다.
위의 식에서 -log4를 일부러 빼주고 +log4를 더해주는데 이는 나중에 JSD(Jensen-Shannon divergence)를 사용하기 위해 즉, 계산의 편의성을 위해 사용한다.
여기서 잠깐!
KL(A || B) : A와 B의 distribution의 차이를 말한다.
JSD(Jensen-Shannon divergence)의 특징
- JSD를 통해 나온 값은 항상 0이상이다.
- 두 개의 distribution이 동일할 때 0이 된다.
그리고
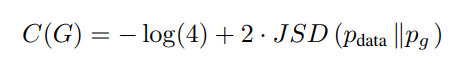여기서 JSD에 2가 곱해져 있는 것을 볼 수 있는데, 이는 원래 JSD에는 전체 식에 (1/2)이 곱해져 있다. 이를 원식과 같게 만들어주기 위해 2를 곱해준다.
Pg = Pdata가 같으면 -log4가 나오는 이유는 다음과 같다. JSD를 통해 Pdata와 Pg의 확률 분포가 같아지면 0이 되므로 Pg = Pdata일 경우 C(G) = -log4 가 나올 수 밖에 없다.
Proposition 2
아직 공부를 더해야 이해할 것 같습니다. 이부분은 뭔가 어렵네요.. ㅠㅠ
이 과정은 앞서 보여드린 알고리즘으로 V(G, D)를 최적화 시켜 원하는 결과를 얻는 과정인데, 이를 실제로 보여주기 위해선 Proposition 2를 추가로 사용하여 한다고 한다.
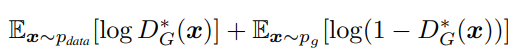집합부터 시작해서 제대로 이해할려면 시간투자를 해야할 것 같습니다. 조금 어렵네요..ㅠㅠ
Experiments
여기서부턴 성능에 대한 얘기를 한다. 이는 paper을 훑어보면 좋을 것 같다.
