오늘은 벡터에 대해 설명해 보려고 한다.
간간히 인공지능에 필요한 수학들에 대한 개념(?)들을 작성해보려고 한다. 기본적으로 미적분, 선형대수, 확률과 통계 등이 있는데, 정말 인공지능을 하기 위한 최소한의 수학을 복습하는 겸 작성해보려고 한다.
시작해보자!!👍
벡터(Vector)
1.1벡터는 무엇일까?
보통 이과계열이면 C언어라는 프로그래밍을 다들 한번 접해봤을 것이라 생각한다. 이때 배열(array)을 배우게 되는데, 이 또한 벡터이다. 벡터의 정의는 다음과 같다.
벡터 : 여러 개의 Data를 한 줄에 담아내는 것.
배열도 이와 다를 것이 없다. 여러 개의 데이터를 하나의 열에 담아두는 것이기 때문이다.
벡터에는 두 가지 종류가 있다.
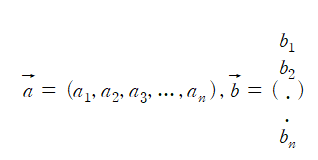
a벡터는 행벡터, b벡터는 열벡터라고 한다.
1.2 벡터의 덧셈, 뺄셈, 스칼라
이 벡터는 어떤 식으로 계산할까?
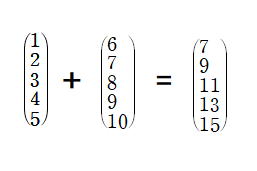 보는 바와 같이 서로 대응하는 성분끼리 덧셈을 합니다. 뺄셈도 마찬가지 입니다. 같은 성분끼리 뺄셈을 합니다. 여기서 중요한 개념이 나오는데,
보는 바와 같이 서로 대응하는 성분끼리 덧셈을 합니다. 뺄셈도 마찬가지 입니다. 같은 성분끼리 뺄셈을 합니다. 여기서 중요한 개념이 나오는데,
벡터 성분의 수 : 차원
위의 그림을 보면 하나의 벡터 성분의 수가 5개 이다. 이 열벡터를 5차원이라고 한다. 따라서 차원이 다르게 되면 덧셈, 뺄셈을 전혀 할 수 없다. (간단한 파이썬 코딩을 하다보면 shape가 맞지 않다고 오류가 뜰 때가 있는데, 이런 경우에는 차원이 맞지 않아서 계산을 할 수 없다는 오류를 내는 것이다.) 조심해야 한다!!
그럼 스칼라에 대해 알아보자. 스칼라는 크기만 있고 방향이 없는 1차원 값을 의미한다.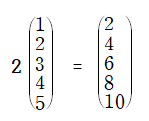
열벡터 앞에 2가 곱해져 있는 것을 볼 수 있는데, 이 2를 스칼라라고 하며 스칼라가 곱해진 것을 보고 스칼라배 라고 한다.
1.3 유향선분
유향선분이라는 것이 또 뭘까 생각하는 사람들이 있을지도 모른다. 쉽게 말해서, 화살표이다. 그럼 어떤 화살표일까? 알아보자!
유향선분 : 방향과 거리를 나타내는 화살표
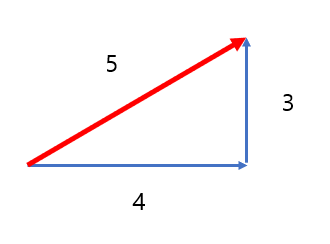 빨간 화살표가 바로 유향선분이다. 이 화살표를 보면 방향과 거리를 알 수 있다는 것이 무슨 말인지 알게 될 것이다. 영어로는 directed segment라고 표현하는데, 종종 영어로 말하는 사람들이 있기도 하니 알아두면 좋다.
빨간 화살표가 바로 유향선분이다. 이 화살표를 보면 방향과 거리를 알 수 있다는 것이 무슨 말인지 알게 될 것이다. 영어로는 directed segment라고 표현하는데, 종종 영어로 말하는 사람들이 있기도 하니 알아두면 좋다.
1.4 내적
어떻게 보면 선형대수에서 내적을 모른다면 공부할 필요가 없을 만큼 중요한 개념이다. 딥러닝이나 인공지능을 하다보면 벡터로 돌린다는 말이 있다. 대부분의 계산들을 벡터로 한다는 얘기이다. 성분들을 곱하고 더하면 for문을 사용하여 계산하면 된다고 생각하지만, 이는 내적보다 시간이 더 오래걸린다. 즉, 기본 중의 기본이라고 생각해야 한다.
내적이 뭔지 알아보자.
내적 : 벡터에서 서로 대응하는 성분끼리 곱한 다음, 그것들을 모두 더한 것.
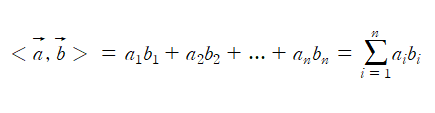 수학적인 수식으로 보면 위의 수식과 동일하다. (여담으로 MSE를 보면 비슷한 꼴이다. 오차를 제곱하고 더한다. 뭔가 비슷하지 않은가? 이 또한 내부적으로 반복문을 써서 계산하는 것이 아니라 내적을 이용해 돌리는 것.)
수학적인 수식으로 보면 위의 수식과 동일하다. (여담으로 MSE를 보면 비슷한 꼴이다. 오차를 제곱하고 더한다. 뭔가 비슷하지 않은가? 이 또한 내부적으로 반복문을 써서 계산하는 것이 아니라 내적을 이용해 돌리는 것.)
이 내적을 기하학적인 측면에서 보면 다음과 같다.
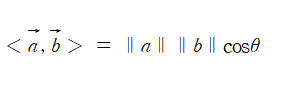
예를 들어 a = (2, 1) , b = (1, 3)의 두 벡터로 이루어졌다고 가정해보자. 이 두 벡터의 사잇값 (θ)는 45도 이다. 이 둘의 계산 과정은 다음과 같다.
(2 x 1 ) + (1 x 3) = 5 이 나온다.
여기서 또 중요하게 알아야 할 것은 두 벡터의 내적의 값은 벡터가 아니라 스칼라다. 두 벡터를 내적했더니 5라는 스칼라가 나오게 된 것이다.
기하학 공식을 이용해보면
(루트5) x (루트10) x cos45 = 5로 동일한 스칼라 값이 나오는 것을 확인할 수 있다.
또 ||a||같은 경우 모두 알겠지...? 이는 유클리드 거리를 의미한다. 유클리드 거리에 대해 나중에 따로 작성을 할 수도 있지만 지금 잘 모르겠다면 구글에 검색하면 바로 알 수 있다. 쉽게 말하자면 한 점과 한점 사이의 거리이다.
1.5 직교 조건(내적)
직교 조건을 확인하는 것은 매우 쉽다. 두 벡터를 내적했는데, 값이 0 이나오면 무조건 두 벡터는 직교하는 것이다. 이러한 이유는 위에서 보았듯이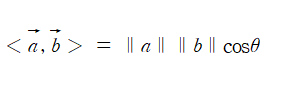 이와 같은 공식 때문이다. 삼각함수에 대해 알면 바로 이해하기 쉽다. 두 벡터가 내적한다는 것은 θ값이 90도 라는 것을 의미하며, cos90 = 0 이라는 것을 눈치챘을 것이다. 두 벡터의 유클리드 거리가 몇이 나오던 간에 cos90을 곱하게 되면 0이 나오는 것이다.
이와 같은 공식 때문이다. 삼각함수에 대해 알면 바로 이해하기 쉽다. 두 벡터가 내적한다는 것은 θ값이 90도 라는 것을 의미하며, cos90 = 0 이라는 것을 눈치챘을 것이다. 두 벡터의 유클리드 거리가 몇이 나오던 간에 cos90을 곱하게 되면 0이 나오는 것이다.
1.6 벡터의 노름(norm)
이 노름(norm)이 말이 참 많다. 어떻게 발음을 해야하는가에 대해서 말이다. ㅋㅋㅋ 누군가는 노름이라고 발음하거나 놂으로 발음하는 사람도 있다. 이 norm도 두가지 경우가 있는데, 한번 살펴보자.
L1 norm : 벡터 성분의 절댓값을 모두 더해서 나온 값
L2 norm : 벡터의 유클리드 거리로 나온 값
이것이 무슨 말이냐 하면 그림으로 이해해보자.
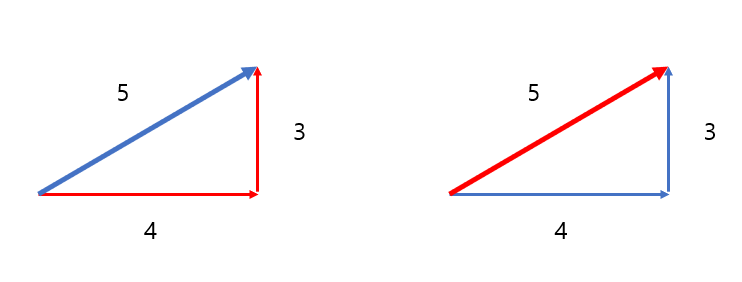
왼쪽은 L1 norm을 설명하기에 좋고, 오른쪽은 L2 norm을 설명하기에 적합하다.우선 L1 norm부터 설명하도록 하겠다. L1 norm 의 수식은 다음과 같다.
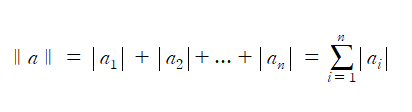
L1 norm은 유클리드 거리와 달리 벡터 성분의 절댓값을 더하는 것이다. 따라서 L1 norm = 4 + 3 = 7이 나오게 된다.즉, 서로 다른 두 지점간의 최단 거리를 의미한다. ("여기서 엥 그게 무슨 말이죠? 그럼 5가 정답이 아닌가요?" 라고 질문하는 사람이 있을지도 몰라 답을 남긴다. 물론 5가 최단거리라고 생각할 수 있다. 하지만, 바둑판을 생각해 보자. 검은색으로 칠해진 줄만 움직일 수 있다고 생각하자. 어찌저찌해도 결국엔 최단거리가 가로 세로의 합이다.) 이해가 안되면 실제 바둑판으로 보고 생각해 보라.
L2 norm의 수식은 다음과 같다.
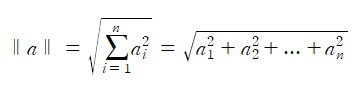
L2 norm은 유클리드 거리이다. 또 쉽게 말하면 피타고라스의 정리라고 생각하면 된다.
1.7 코사인 유사도
이건 또 뭐냐!! 라고 하면 지금까지 배운 내용들에 다 포함되어 있다. 내적하고 유클리드 거리 같은 경우에는 구하기 정말 쉬운데 cos(θ)는 뭔가 구하기 어렵다는 것이지.. 근데 지금까지 우리가 배운 내용들로 cos(θ)값은 충분히 구할 수 있다.
위의 공식들을 이용해 수식을 정의해보자.
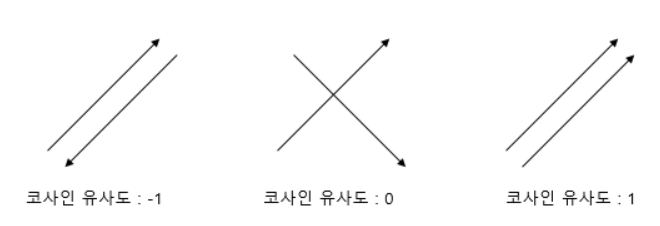
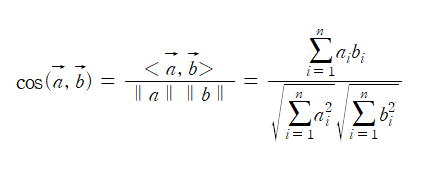 뭔가 익숙해 보이지 않은가? 이항해서 cos(θ)값만 가져온 것이다. 이 cos(θ)는 -1과 1사이에 존재한다.
뭔가 익숙해 보이지 않은가? 이항해서 cos(θ)값만 가져온 것이다. 이 cos(θ)는 -1과 1사이에 존재한다.
-1 : 방향은 다르지만 평행하다.
0 : 직교한다.
1 : 방향도 동일하고 평행하다.