벡터에 대해 어느정도 알았다면 벡터의 아버지(?) 느낌이 나는 행렬에 대해 알아보자. 굳이 저렇게 표현한 이유는 여러개의 벡터를 하나의 행렬로 표현이 가능하여 그렇게 한것이다.
행렬에 대한 기초같은 경우에는 이 블로그에서 매우 자세하게 설명했다.
https://gosamy.tistory.com/3
한번 읽고 오길 바란다.
행렬
2.1 역행렬
행렬의 덧셈, 뺄셈, 곱셈, 정방행렬, 단위행렬 등의 개념과 풀이에 대해 자세히 알아야 한다.
저 블로그에서 역행렬에 대해 설명했는데, 이해가 될진 모르겠다. 좀더 쉽게 설명해 보겠다.
역행렬을 사용하는 이유는 나눗셈 때문이다. 사칙연산을 보면 덧셈, 뺄셈, 곱셈, 나눗셈이 존재하는데, 행렬에는 나눗셈이 존재하지 않는다. 그래서 역수를 취하고 곱함으로써 나눗셈의 역할을 대신하는 것이다. 이게 무슨 내용인지 알아보자.
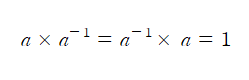이 식이 뭔지 기억이 나겠지? 1을 만들때 우리가 종종 사용하는 수식이다. 이처럼 역행렬을 이용하여 1을 만들어 보자.
행렬에는 역행렬이 존재할 수도 있고 아닐수도 있다. 그래서 무작정 역행렬을 구하는 공식을 사용해서 계산했다가 큰코 다칠 수 있다. 그래서 행렬식(determinant)를 사용해서 역행렬이 존재하는지부터 확인해 보도록 하자.
행렬식은 다음과 같다.
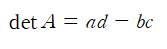
별거 아니지만 중요하다. 먼저 행렬식으로 확인하자. 행렬이 좀 복잡하면 겁나게 귀찮아지는데, 계산했는데 역행렬 안나오면 매우 화가나지 않겠는가?
행렬식을 구했는데 0이 나온다면 그 행렬의 역행렬은 존재하지 않는다는 것이다. 만약 0이 아니라면 해당 행렬의 역행렬은 존재한다는 뜻이므로 그때 역행렬 공식을 사용하여 구하면 된다.
역행렬을 구하는 공식은 다음과 같다.
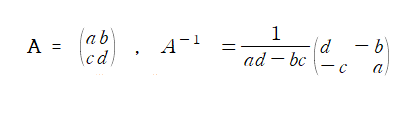
2.2 선형 변환
"행렬은 선형변환이다!" --> (입력을 넣어주면 출력이 달라지는 함수같은 개념)
이번에는 선형 변환이 무엇인지 이해해보도록 하자. 쉽게 말하자면 하나의 벡터에 행렬을 곱해 다른 벡터를 만드는 것을 의미한다. 이를 표현하면 다음과 같다.
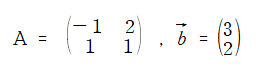
A라는 행렬에 벡터 b를 곱하면 어떻게 되나?
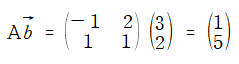
2 x 1 을 갖는 하나의 벡터가 나오는 것을 볼 수 있다. 보통 선형변환을 설명할 때, 표준기저 혹은 기저에 대한 내용이 나오는데, 이 기저가 무엇인지 살펴보자.
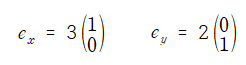벡터 b를 위의 그림과 같이 표현할 수 있다.
위의 1)행렬 A와 벡터 b를 행렬곱으로 구한 결과와 2) 행렬 A와 기저벡터를 이용해 나온 벡터값의 행렬곱의 결과는 서로 같다.
이때 나온 결과는 벡터를 회전하거나 확대, 또는 축소시킨 것과 같은 효과른 내고 있다.
결론을 내보자!! 어떤 벡터의 왼쪽에다 행렬 A를 곱한다는 것은 그 벡터를 다른 벡터 공간으로 변환하고자 회전하거나 확대, 또는 축소하는 것과 같다. 이를 선형변환이라 한다.
+)간단하게 DNN을 돌릴 때 계산과정을 생각해보자. 가중치는 행렬이고 input x는 벡터이다. 이를 곱하고 bias를 더하는 계산과정을 같지 않는가? 이 경우 선형변환에 해당되는 것이다.
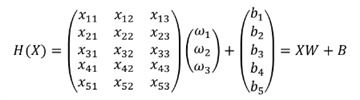이 그림을 보자. 어떤 벡터 왼쪽에 하나의 행렬을 곱하고 bias를 더해 나오는 계산을 볼 수 있는데, 이 같은 경우도 선형 변환이다. 좀더 이해를 돕기 위해 그림을 첨부하고 끝내겠다.
2.3 고윳값과 고유벡터
고윳값과 고유벡터도 선형변환데 대해 알아야 쉽게 이해할 수 있는 부분이다. 하나의 벡터에 행렬을 곱하여 선형변환이 이루어진다고 가정하자. 근데, 선형변환을 했는데 크기만 바뀌고 방향이 동일한 경우가 생길때가 있다. 이처럼 말이다.
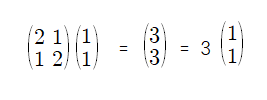
정의로만 보면 다음과 같다.
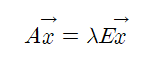
정방행렬 A와 열벡터 x(x != 0)이 존재하면, λ는 행렬 A의 고윳값이라하고 x를 고유벡터라 한다.
즉, 고윳값과 고유벡터가 물어보는 것은
- 벡터 x에 선형변환 A를 했을 때, 그 크기만 변하고 원래 벡터와 평행한 벡터 x는 무엇인가?
- 크기는 얼마나 변했는가?
에 대한 문제를 풀기 위해 고윳값과 고유벡터를 구하는 것이다.
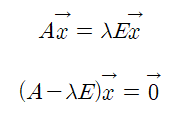이와 같이 왼쪽으로 이항하면 우항은 0벡터가 나오는 꼴로 된다. 이때, 전제 조건을 살펴봐야 하는데, 열벡터 x는 절대로 0이 되어서는 안된다. 이를 만족하기 위해선,
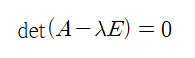이를 만족해야 한다. 역행렬이 생각나는가? 만약 역행렬이 존재한다면 det(A - λE)는 0이 될 수 없다. 그럼 열벡터 x가 0이 되어야 하는데 전제조건과는 틀려지니, det(A - λE)가 무조건 0이 되어야 한다. 따라서 이 과정이 필요하다.
이렇게 계산을 하게 되면 λ에 대한 2차 방정식이 나오게 된다. 이를 풀어서 2개의 λ근을 얻을 수 있다.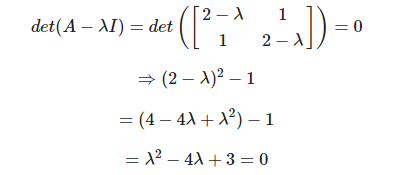 
이를 전의 식에 대입하여 풀어보면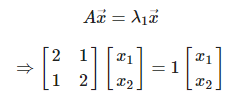 
이 나오게 된다. 각 고윳값이 다르므로 λ1과 λ2의 값을 넣어 각각 계산해주어야 한다. 
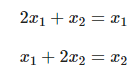위의 그림에서 λ1을 넣으면 
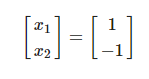λ2를 넣어 계산하면 
이로써 고윳값과 고유벡터에 대한 설명은 끝이 났다. 이는 비지도 학습에서 주성분 분석(PCA) 기법을 사용하는데 다차원 데이터를 2,3차원으로 압축하는 방법이다. 데이터가 많이 흩어져 있는 상황에서는 고윳값과 고유벡터의 개념을 사용하게 된다.
