
1. 깊이 우선 탐색(DFS, Depth-First Search)
DFS는 깊이 우선 탐색이라고 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘입니다.
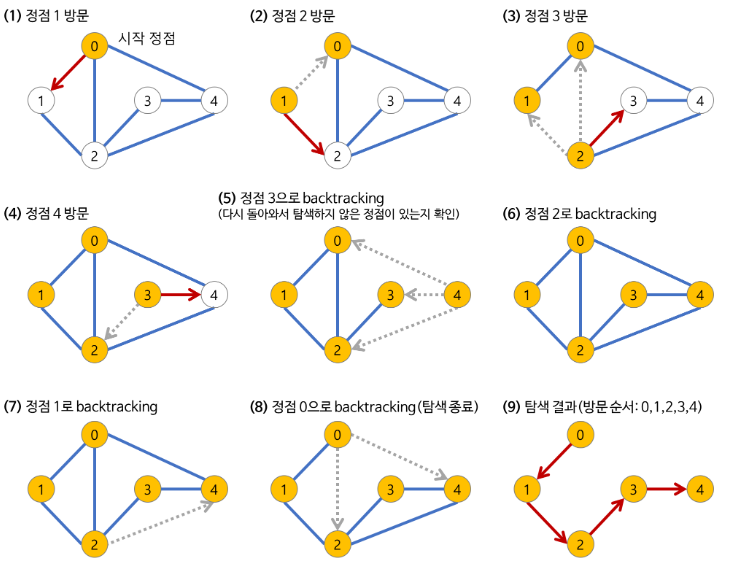
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리합니다.
2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리합니다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼냅니다.
3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복합니다.
2. 깊이 우선 탐색의 장단점
장점
1. 현재 경로상의 노드들만 기억하면 되므로 저장 공간의 수요가 비교적 적음
2. 목표 노드가 깊은 단계에 있는 경우 해를 빨리 구할 수 있음
3. BFS 보다 구현이 간단함
단점
1. 단순 검색 속도가 BFS 보다 느림
2. 해가 없는 경우에 빠질 수 있음. 따라서 사전에 탐색할 임의의 깊이를 지정할 필요가 있다.
3. DFS는 해를 구하면 탐색이 종료된다. 따라서 구한 해가 최적의 해가 아닐 수 있다.
3. 깊이 우선 탐색의 구현
구현 방법 2가지
1. 순환 호출 이용
def dfs_recursive(graph, start, visited = []):
## 데이터를 추가하는 명령어 / 재귀가 이루어짐
visited.append(start)
for node in graph[start]:
if node not in visited:
dfs_recursive(graph, node, visited)
return visited2. 명시적인 스택 사용
def dfs2(graph, start_node):
## deque 패키지 불러오기
from collections import deque
visited = []
need_visited = deque()
##시작 노드 설정해주기
need_visited.append(start_node)
## 방문이 필요한 리스트가 아직 존재한다면
while need_visited:
## 시작 노드를 지정하고
node = need_visited.pop()
##만약 방문한 리스트에 없다면
if node not in visited:
## 방문 리스트에 노드를 추가
visited.append(node)
## 인접 노드들을 방문 예정 리스트에 추가
need_visited.extend(graph[node])
return visited깊이 우선 탐색(DFS)의 시간 복잡도
그래프를 인접 행렬(adjacency matrix)로 구현했는지, 인접 리스트(adjacency list)로 구현했는 지에 따라 구현방법이 달라진다.
인접 행렬(adjacency matrix)로 구현
vector<vector<int>> adjacent; //인접 행렬로 구현된 그래프 들어감
vector<bool> visited; // 그래프의 정점만큼의 크기로 생성
void DFS(int now)
{
visited[now] = true;
int N = adjacent.size();
for (int i = 0; i < N; i++)
{
if (adjacent[now][i] == 0)
continue;
if (!visited[i])
DFS(i);
}
}DFS 하나당 N번의 loop를 돌게 되므로 O(n)의 시간복잡도를 가진다. 그런데 N개의 정점을 모두 방문 해야하므로
n*O(n)이므로 O(n^2)의 시간복잡도를 가지게 된다.따라서 O(n^2)의 시간복잡도를 가지게 된다.
인접 리스트(adjacency list)로 구현
vector<vector<int>> adjacent; //인접 리스트로 구현된 그래프 들어감
vector<bool> visited; // 그래프의 정점만큼의 크기로 생성
void DFS(int now)
{
visited[now] = true;
for (int i = 0; i < adjacent[now].size(); i++)
{
int next = adjacent[now][i];
if (!visited[next])
DFS(next);
}
}DFS가 총 N번 호출되긴 하지만 인접행렬과 달리 인접 리스트로 구현하게 되면 DFS하나당 각 정점에 연결되어 있는 간선의 개수만큼 탐색을 하게 되므로 예측이 불가능 하다. 하지만 DFS가 다 끝난 후를 생각하면, 모든 정점을 한번씩 다 방문하고, 모든 간선을 한번씩 모두 검사했다고 할 수 있으므로 O(n+e)의 시간이 걸렸다고 할 수 있다.
따라서 시간복잡도는 O(n+e)이다.
- 즉, 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.
참고문헌
https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html
https://velog.io/@cha-suyeon/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B9%8A%EC%9D%B4-%EC%9A%B0%EC%84%A0-%ED%83%90%EC%83%89DFS-%EA%B3%BC-%EB%84%88%EB%B9%84-%EC%9A%B0%EC%84%A0-%ED%83%90%EC%83%89BFS
https://currygamedev.tistory.com/10
https://data-marketing-bk.tistory.com/44
