1. 계수 정렬

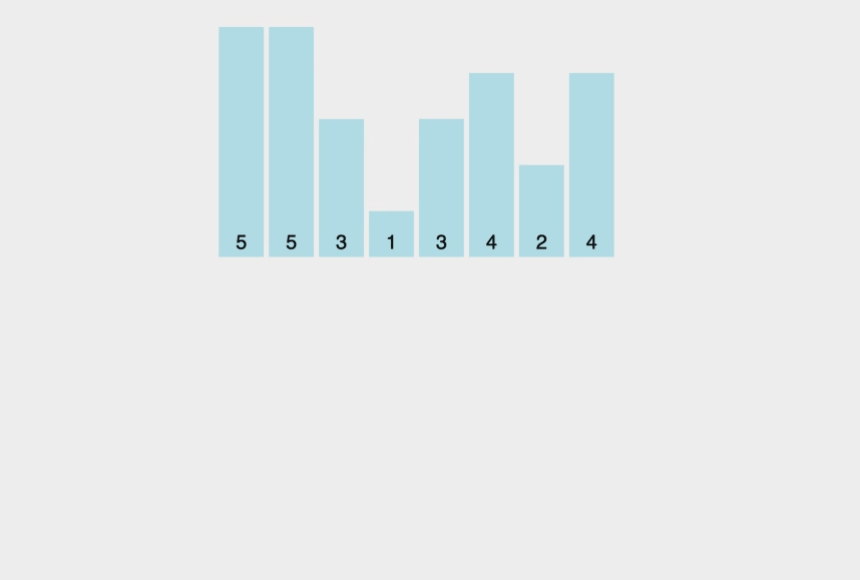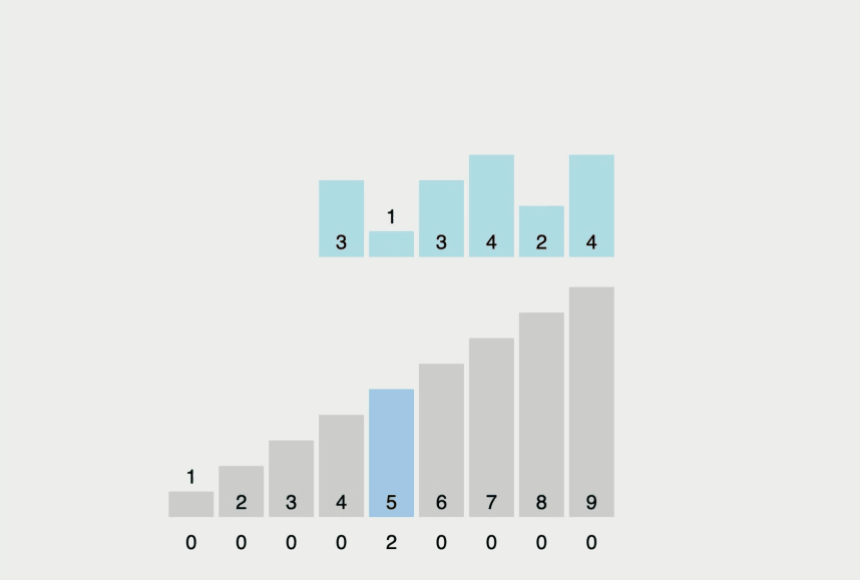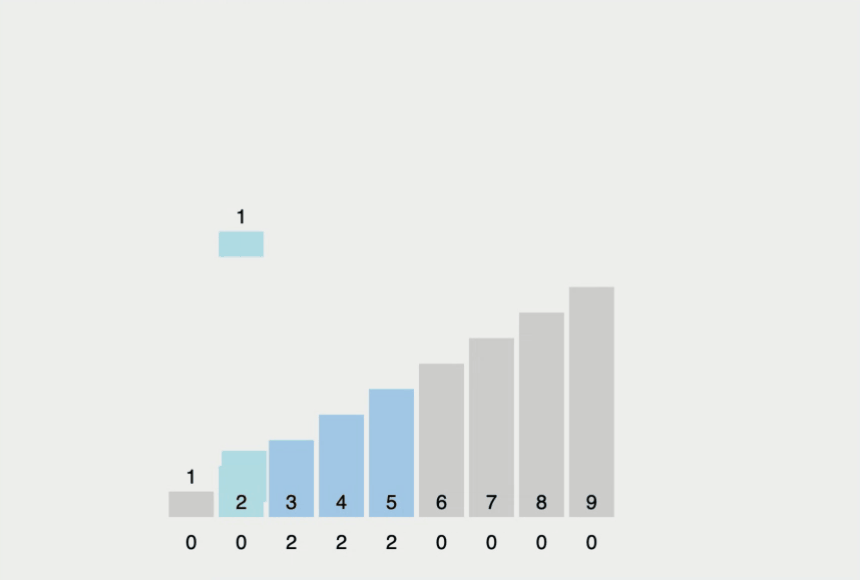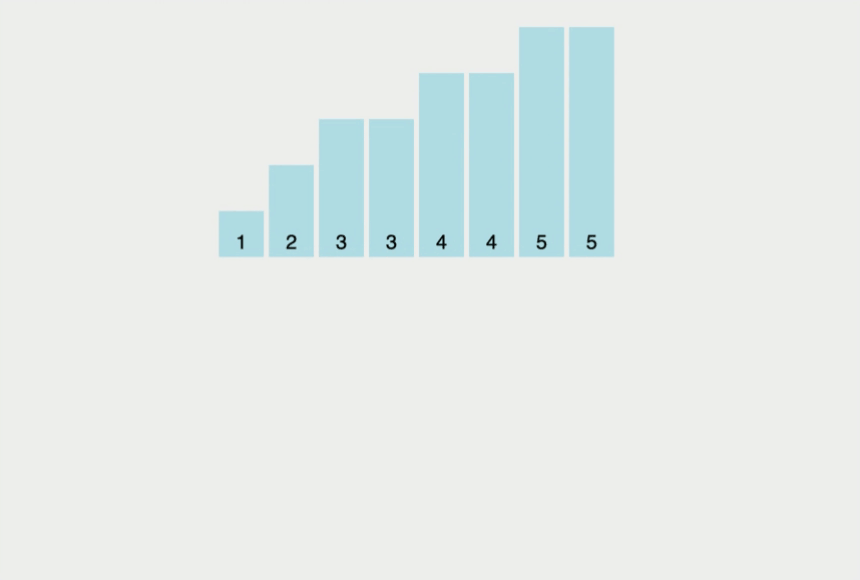
계수 정렬은 특정한 조건이 부합할 때만 사용할 수 있지만, 매우 빠르게 동작하는 정렬 알고리즘이다. (여기서 특정한 조건이란 계수 정렬은 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용이 가능.)

• 일반적으로 가장 큰 데이터와 가장 작은 데이터의 차이가 1,000,000을 넘지 않을 때 효과적으로 사용할 수 있다.
• 계수 정렬은 동일한 값을 가지는 데이터가 여러개 등장할 때 효과적으로 사용할 수 있다. (Ex) 학생들의 성적, 자동차들의 속도 데이터

2. 계수 정렬 장단점

장점

• 이 정렬법도 비교를 하지 않고 정렬하는 법으로 O(N) 이라는 시간복잡도를 갖게 된다.
• 일단, O(N)이라는 것 자체만으로도 정렬법 중에서 엄청나게 빠른 편에 속하고 이것이 장점으로 작용한다.

단점

• 숫자 갯수를 저장해야 될 별도의 공간, 또 결과를 저장할 별도의 공간 등 추가적인 메모리가 필요하다.
• 또한, 하나의 값 때문에 메모리의 낭비를 많이 하게 될 수도 있다. 예를 들면 다음과 같은 경우이다.
  [ 1, 2, 3, 4, 5, 99999999999 ] 이 경우에는 99999999999 때문에 숫자의 갯수를 저장해야 될 배열의 크기가 최소 [ 99999999999 ] 보다는 커야 하고, 결과적으로 안 쓰는 낭비되는 인덱스들이 많이 발생하게 된다.

3. 계수 정렬 구현

구현

# 계수 정렬을 사용하여 오름차순 정렬
# 단, 리스트의 모든 원소의 값이 0보다 크거나 같다고 가정
arr = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
# 모든 범위를 포함하는 리스트 선언 (모든 값을 0으로 초기화)
count = [0] * (max(arr) + 1)

for a in arr:
    # 각 데이터에 해당하는 인덱스의 값 증가
    count[a] += 1

# 리스트에 기록된 정렬 정보 확인
for i in range(len(count)):
    for j in range(count[i]):
        # 띄어쓰기를 구분으로 등장한 횟수만큼 인덱스 출력
        print(i, end=' ')

>>> 0 0 1 1 2 2 3 4 5 5 6 7 8 9 9 

시간 복잡도 및 공간 복잡도

- 시간 복잡도는 데이터의 개수가 N, 데이터(양수) 중 최댓값이 K일 때 최악의 경우에도 O(N+K)를 보장한다.

k가 정렬할 수들 중에 가장 큰 값을 의미하는데요. 만약 k가 n보다 작은 수이면 O(n)이 되지만, k가 n보다 매우 큰 수이면 O(무한)이 될 수도 있습니다.
예를 들어 10개의 숫자를 정렬하는 데, 가장 큰 숫자가 100일 경우, O(n^2)이 됩니다. 100(k)은 10(n)의 제곱이니까요.
1000이면 O(n^3)이 되죠. 즉 정렬할 수들의 최대값에 영향을 받는 알고리즘이라고 볼 수 있습니다.

- 공간 복잡도는 데이터의 개수가 N, 데이터(양수) 중 최댓값이 K일 때 O(N+k)이다.

공간 복잡도는 k만큼의 배열을 추가로 만들어야 하기 때문에 O(N+k)라고 할 수 있다.

참고문헌

https://yabmoons.tistory.com/250
https://velog.io/@kimdukbae/%EC%A0%95%EB%A0%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Sorting-Algorithm
https://computer-science-student.tistory.com/587
https://ssungkang.tistory.com/entry/Algorithm-Counting-Sort-%EA%B3%84%EC%88%98-%EC%A0%95%EB%A0%AC