1. 퀵 정렬

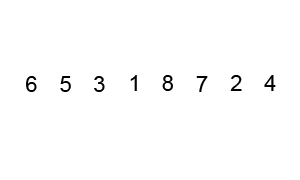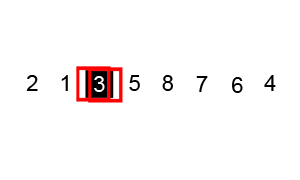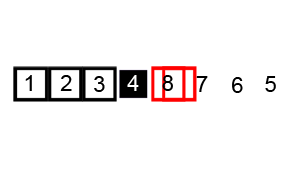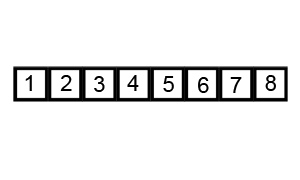
퀵 정렬은 기준 데이터(pivot)를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 정렬 방법이다.

일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나이며, 병합 정렬과 더불어 대부분의 프로그래밍 언어의 정렬 라이브러리의 근간이 되는 알고리즘이다.

2. 퀵 정렬 장단점

장점

• 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문에, 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
  
• 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다.

단점

• 기준값(Pivot)에 따라서 시간복잡도가 크게 달라진다. Pivot이 적당하게 이상적인 값을 선택했다면 O(NlogN)의 시간복잡도를 갖지만, 최악으로 Pivot을 선택할 경우(최소나 최대값) O(N^2) 이라는 시간복잡도를 갖게 된다.

3. 퀵 정렬 구현

일반적인 구현

# 퀵 정렬을 사용하여 오름차순 정렬
arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]


def quick_sort(array, start, end):
    if start >= end:  # 원소가 1개인 경우 종료
        return
    pivot = start  # 피벗은 첫 번째 원소
    left = start + 1
    right = end
    while left <= right:
        # 피벗보다 큰 데이터를 찾을 때까지 반복
        while left <= end and array[left] <= array[pivot]:
            left += 1
        # 피벗보다 작은 데이터를 찾을 때까지 반복
        while right > start and array[right] >= array[pivot]:
            right -= 1
        if left > right:  # 엇갈렸다면 작은 데이터와 피벗을 교체
            array[right], array[pivot] = array[pivot], array[right]
        else:  # 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
            array[left], array[right] = array[right], array[left]
    # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
    quick_sort(array, start, right - 1)
    quick_sort(array, right + 1, end)


quick_sort(arr, 0, len(arr) - 1)
print(arr)

>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

파이썬의 장점을 이용한 특별한 구현

# Python의 장점을 살린 퀵 정렬
def quick_sort_better(array):
    # 리스트가 하나 이하의 원소만을 담고 있따면 종료
    if len(array) <= 1:
        return array

    pivot = array[0]  # 피벗은 첫 번째 원소
    tail = array[1:]  # 피벗을 제외한 리스트

    left_side = [x for x in tail if x <= pivot]
    right_side = [x for x in tail if x > pivot]

    # 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
    return quick_sort_better(left_side) + [pivot] + quick_sort_better(right_side)


print(quick_sort_better(arr))

>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

시간복잡도

시간 복잡도는 평균의 경우 O(NlogN)이고, 최악의 경우 O(N^2)의 시간 복잡도를 가진다.

최선의 경우(Best cases) : T(n) = O(nlog₂n)

• 비교 횟수 (log₂n)

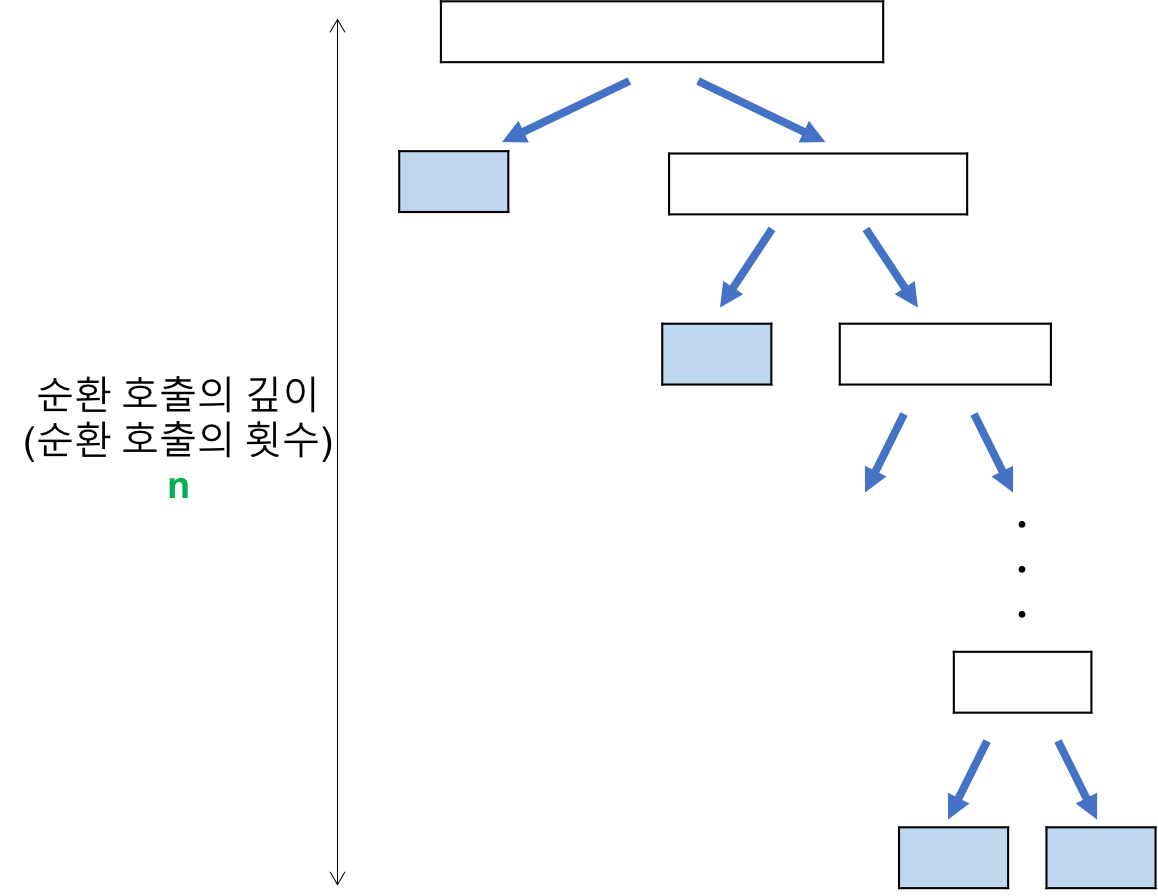
  레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k) 했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다.
  
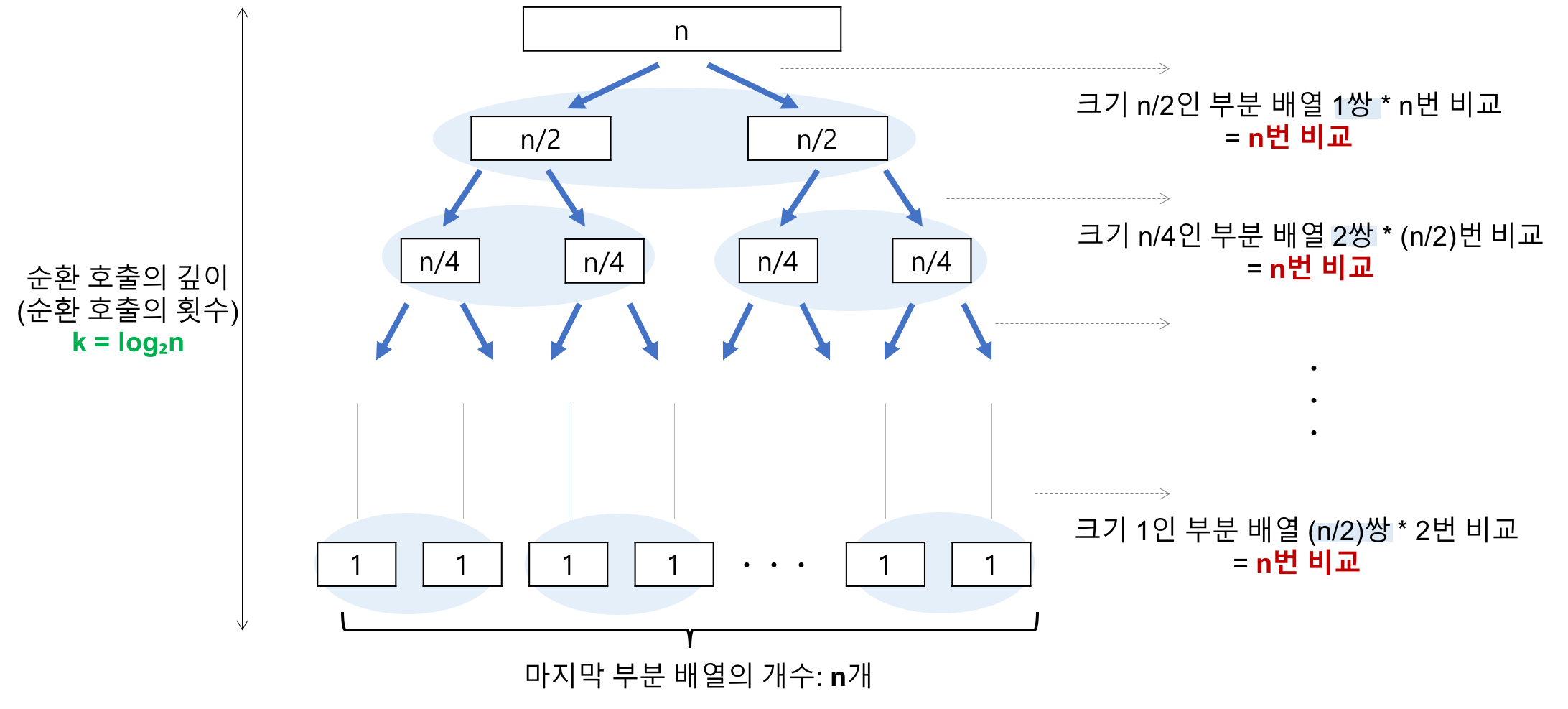
  이것을 일반화하면 n=2^k의 경우, k(k=log₂n) 임을 알 수 있다.

• 각 순환 호출 단계의 비교 연산 (n)

  각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.

따라서, 최선의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n 가 된다. 이동 횟수는 비교 횟수보다 적으므로 무시할 수 있다.

최악의 경우(Worst cases) : T(n) = O(n^2)

최악의 경우는 정렬하고자 하는 배열이 오름차순 정렬되어있거나 내림차순 정렬되어있는 경우다.

• 비교 횟수 (n)

레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n 임을 알 수 있다.

• 각 순환 호출 단계의 비교 연산 (n)

각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.

따라서, 최악의 시간복잡도는 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2 다. 이동 횟수는 비교 횟수보다 적으므로 무시할 수 있다.

참고문헌

https://velog.io/@kimdukbae/%EC%A0%95%EB%A0%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Sorting-Algorithm
https://yabmoons.tistory.com/250
https://gyoogle.dev/blog/algorithm/Quick%20Sort.html