
1. 라빈-카프 알고리즘
라빈-카프 알고리즘은 문자열에 해싱 기법을 사용하여 해시 값으로 비교하는 알고리즘이다.
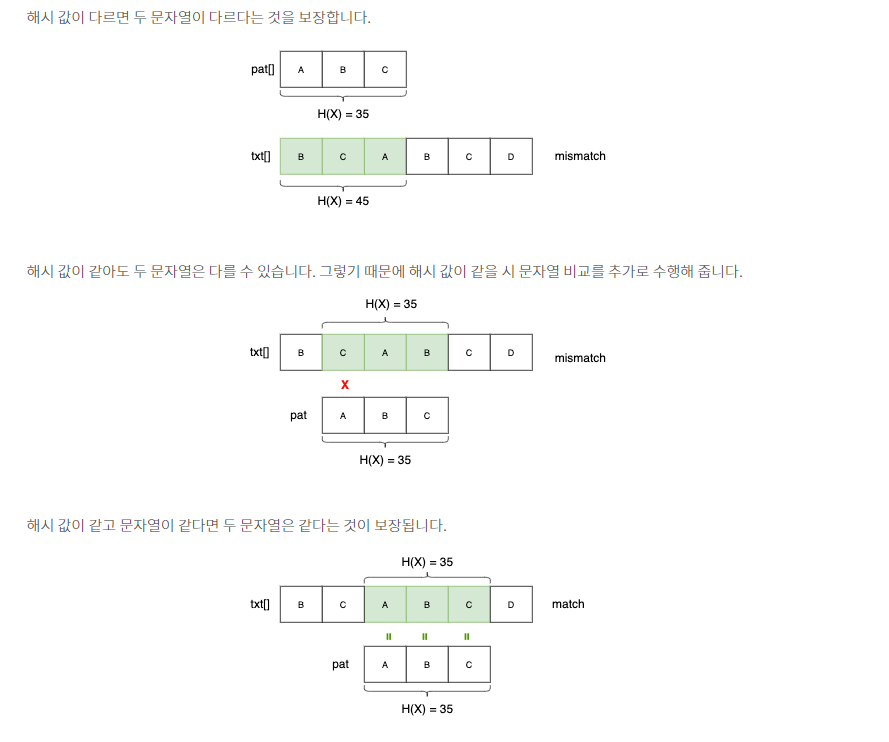
해시 값이 다르다면 두 문자열은 다르다는 것이 보장된다. 하지만 문자열이 달라도 해시 값이 같을 수 있다.
우리는 이것을 Spurious Hit라고 부른다.
Spurious Hit 때문에 해시 값이 같을 경우 추가로 문자열이 같은지 비교하는 작업이 필요하다. 이 특징을 사용하여 Rabin-Karp 알고리즘은 패턴의 해시값을 텍스트의 부분 문자열의 해시 값과 일치하는지 비교하는 작업을 한다.
따라서 Rabin-Karp 알고리즘은 다음 문자열에 대한 해시 값을 계산해야 한다.
- 길이가 m인 패턴 자체
- 길이가 m인 텍스트의 모든 부분 문자열.
2. 해시 함수
사용 예시

rolling hash
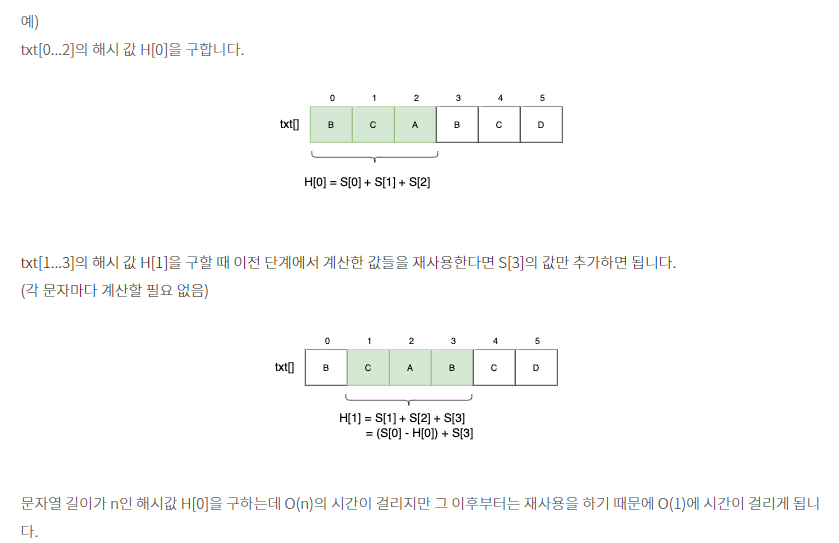
각 위치에서 해시 함수를 처음부터 다시 계산하는 것은 너무 느립니다. 그렇기 때문에 rolling hash를 사용합니다.
rolling hash는 window 사이즈만큼 이동하면서 입력을 받아 해시값을 구합니다.
rolling hash를 통해 사용했던 결과를 재사용해서 해시 값을 빠르게 계산할 수 있습니다. (메모라이즈 기법 사용)
3. 라빈-카프 알고리즘 구현
일반적인 구현
def find_string(parent, pattern):
parent_len = len(parent)
pattern_len = len(pattern)
parent_hash = 0
pattern_hash = 0
power = 1
for i in range(parent_len - pattern_len + 1):
if i == 0:
for j in range(pattern_len):
parent_hash += ord(parent[pattern_len - 1 - j]) * power
pattern_hash += ord(pattern[pattern_len - 1 - j]) * power
if j < pattern_len - 1:
power *= 2
else:
parent_hash = 2 * (parent_hash - ord(parent[i - 1]) * power) + ord(parent[pattern_len - 1 + i])
if parent_hash == pattern_hash:
found = True
for j in range(pattern_len):
if parent[i + j] != pattern[j]:
found = False
break
if found:
print(f'{i + 1}번째에서 발견했습니다')
if __name__ == "__main__":
parent = "ababacabacaabacaaba"
pattern = "abacaaba"
find_string(parent, pattern)나머지 연산을 이용한 구현
def find_string(parent, pattern):
parent_len = len(parent)
pattern_len = len(pattern)
parent_hash = 0
pattern_hash = 0
power = 1
for i in range(parent_len - pattern_len):
if i == 0:
for j in range(pattern_len):
parent_hash += ord(parent[pattern_len - 1 - j]) * power
pattern_hash += ord(pattern[pattern_len - 1 - j]) * power
if j < pattern_len - 1:
power *= 403
else:
parent_hash = 403 * (parent_hash - ord(parent[i - 1]) * power) + ord(parent[pattern_len - 1 + i])
if parent_hash == pattern_hash:
found = True
for j in range(pattern_len):
if parent[i + j] != pattern[j]:
found = False
break
if found:
print(f'{i + 1}번째에서 발견했습니다')
if __name__ == "__main__":
parent = "ababacabacaabacaaba"
pattern = "abacaaba"
find_string(parent, pattern)시간복잡도
pattern의 길이를 M, text의 길이를 N이라고 가정하겠습니다.
-
보통 : 전처리 단계의 시간 복잡도는 O(M)이고 문자열 검색 단계의 시간 복잡도는 O(N)이기 때문에 시간 복잡도는 O(M+N)입니다.
(해시 값을 구할 때, 처음 한번 구해놓으면, 다음 해시값을 구할 때는 가장 처음값을 해시값에서 빼주고, 새로 추가된 부분을 해시값에 더해주기만 하면되기 때문) -
최악의 경우 : 해쉬함수가 좋지 않아서 각각 다른 문자열이 공통된 해쉬값을 가질 경우 O(NM)
4. 참고자료
https://yoongrammer.tistory.com/93
https://uiandwe.tistory.com/1345
https://jjudrgn.tistory.com/65
