1. KMP Algorithm

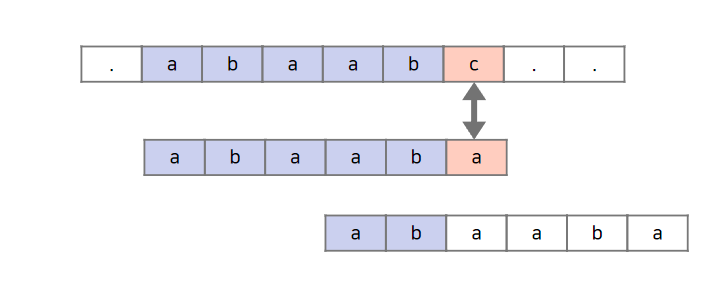
KMP 알고리즘으로 불리는 문자열 매칭 알고리즘이다.

KMP 알고리즘은 패턴을 문장안에서 좌에서 우로 비교하는 것인데, Brute-force 알고리즘과 다르게 패턴의 위치를 좀 더 효율적으로 이동시킨다. 패턴과 문장의 불일치가 발생했을 때 중복연산을 최대한 피하면서 패턴을 우측으로 이동시킨다. 이를 위해서는 문장의 불일치 발생 시, 얼만큼 건너 뛴 후에 비교연산을 할 것인가를 판단하여야 한다.

2. Failure Function / Pi array

실패함수 또는 파이 배열이란?

KMP 알고리즘에서 탐색 문자열의 접두사와 접미사의 일치 부분을 계산하여 배열의 형태로 저장하는 함수이다.

실행 흐름

i 는 접미사 가리키는 인덱스, len은 접두사 가리키는 인덱스입니다.

※ 7번째 붙임설명
6번째에 len = 2, i = 5일 때, A가 이미 일치했던 사실을 알기 때문에 이를 이용하기 위해 len은 lps[len - 1]로 이동하는 것입니다. 이는 KMP 알고리즘 원리와 같습니다.

코드

# KMP 알고리즘을 수행하기 전, 패턴을 처리하는 함수
# 패턴의 테이블 생성
def KMP_table(pattern):
    lp = len(pattern)
    tb = [0 for _ in range(lp)] # 정보 저장용 테이블
    
    pidx = 0 # 테이블의 값을 불러오고, 패턴의 인덱스에 접근
    for idx in range(1, lp): # 테이블에 값 저장하기 위해 활용하는 인덱스
        # pidx가 0이 되거나, idx와 pidx의 pattern 접근 값이 같아질때까지 진행
        while pidx > 0 and pattern[idx] != pattern[pidx]:
            pidx = tb[pidx-1]
        
        # 값이 일치하는 경우, pidx 1 증가시키고 그 값을 tb에 저장
        if pattern[idx] == pattern[pidx] :
            pidx += 1
            tb[idx] = pidx
    
    return tb

3. KMP 알고리즘 구현

Failure Function 에서 만든 테이블을 활용하여 KMP 알고리즘 진행

실행 흐름

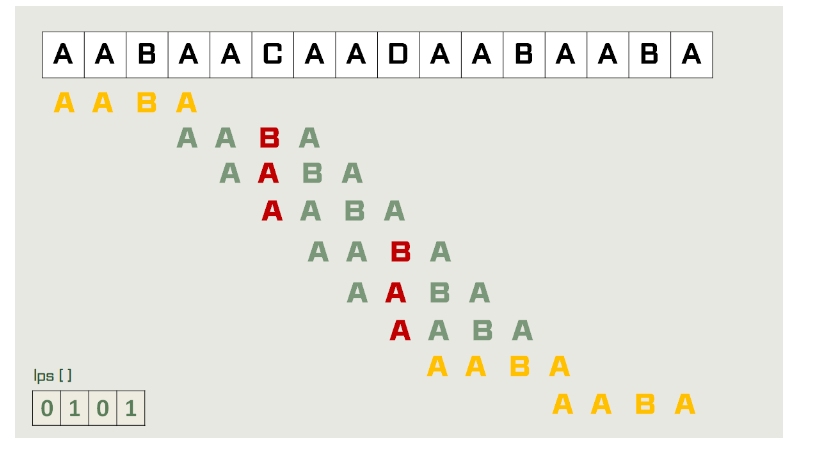
노란색일 때, 일치했을 때이다. 주의 깊게 봐야할 점은 KMP 알고리즘에서는 일치했을 때에도, 불일치했을 때와 마찬가지로 그 전까지는 일치했다는 것을 이용해 몇 글자 건너서 검사를 다시 시작한다.

전체 코드

# KMP 알고리즘을 수행하기 전, 패턴을 처리하는 함수
# 패턴의 테이블 생성
def KMP_table(pattern):
    lp = len(pattern)
    tb = [0 for _ in range(lp)] # 정보 저장용 테이블
    
    pidx = 0 # 테이블의 값을 불러오고, 패턴의 인덱스에 접근
    for idx in range(1, lp): # 테이블에 값 저장하기 위해 활용하는 인덱스
        # pidx가 0이 되거나, idx와 pidx의 pattern 접근 값이 같아질때까지 진행
        while pidx > 0 and pattern[idx] != pattern[pidx]:
            pidx = tb[pidx-1]
        
        # 값이 일치하는 경우, pidx 1 증가시키고 그 값을 tb에 저장
        if pattern[idx] == pattern[pidx] :
            pidx += 1
            tb[idx] = pidx
    
    return tb
    
def KMP(word, pattern):
    # KMP_table 통해 전처리된 테이블 불러오기
    table = KMP_table(pattern)
    
    results = [] # 결과를 만족하는 인덱스 시점을 기록하는 리스트
    pidx = 0
    
    for idx in range(len(word)):
        # 단어와 패턴이 일치하지 않는 경우, pidx를 table을 활용해 값 변경
        while pidx > 0 and word[idx] != pattern[pidx] :
            pidx = table[pidx-1]
        # 해당 인덱스에서 값이 일치한다면, pidx를 1 증가시킴
        # 만약 pidx가 패턴의 끝까지 도달하였다면, 시작 인덱스 값을 계산하여 추가 후 pidx 값 table의 인덱스에 접근하여 변경
        if word[idx] == pattern[pidx]:
            if pidx == len(pattern)-1 :
                results.append(idx-len(pattern)+2)
                pidx = table[pidx]
            else:
                pidx += 1
    
    return results

시간복잡도

KMP 알고리즘에서 접두, 접미사의 길이를 이용하여 탐색을 건너뛰는 아이디어이므로 문자열의 길이에 비례하게 된다.

원본 문자열의 길이가 N, 탐색 문자열의 길이가 M 이라면 최종적인 시간 복잡도는 O(N + M) 이 된다.

참고자료

https://velog.io/@hwan2da/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-KMP-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://bblackscene21.tistory.com/2
https://velog.io/@mein-figur/PythonKMP-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98