1. 삽입 정렬

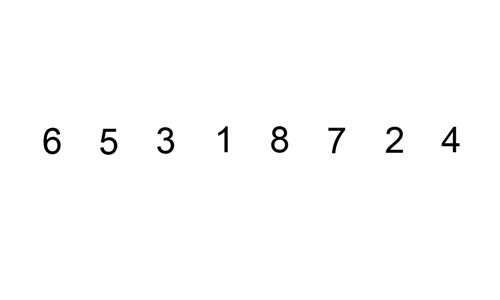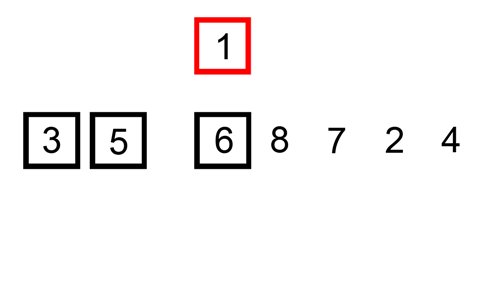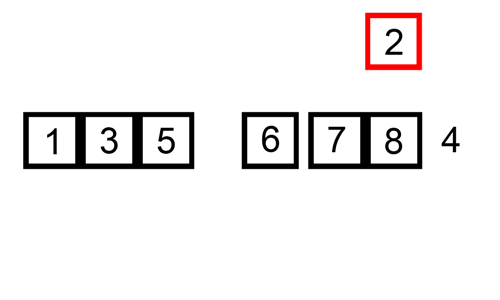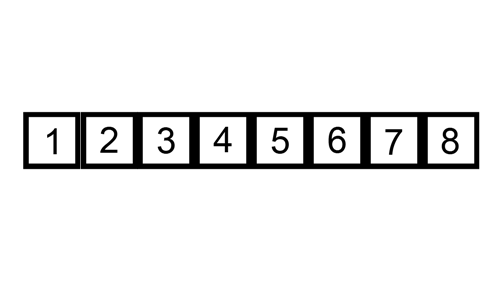
삽입 정렬은 특정한 데이터를 적절한 위치에 삽입한다.

삽입 정렬은 특정한 데이터가 적절한 위치에 들어가기 이전에 그 앞까지의 데이터는 이미 정렬되어 있다고 가정한다. 정렬되어 있는 데이터 리스트에서 적절한 위치를 찾은 뒤에, 그 위치에 삽입된다.
선택 정렬에 비해 구현 난이도가 높은 편이지만, 선택 정렬에 비해 실행 시간 측면에서 더 효율적인 알고리즘으로 잘 알려져 있다.

2. 삽입 정렬 장단점

장점

• 최선의 경우(데이터가 거의 정렬되어 있는 상태) O(N)이라는 엄청나게 빠른 효율성을 가지고 있다.

• 성능이 좋아서 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 정렬법이다.

단점

• 최악의 경우 O(N^2) 이라는 시간복잡도를 갖게된다. 즉, 데이터의 상태 및 데이터의 크기에 따라서

  성능의 편차가 굉장히 심한 정렬법이다.

3. 삽입 정렬 구현

구현

# 삽입 정렬을 사용하여 오름차순 정렬
arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

for i in range(1, len(arr)):
    # 인덱스 i부터 1까지 감소하며 반복
    for j in range(i, 0, -1):
        # 한 칸씩 왼쪽으로 이동
        if arr[j] < arr[j - 1]:
            temp = arr[j]
            arr[j] = arr[j - 1]
            arr[j - 1] = temp
        # 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
        else:
            break

print(arr)

>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

시간복잡도

시간 복잡도는 O(N^2)이다.

선택 정렬과 마찬가지로 2중 반복문 때문에 N^2이다.
삽입 정렬은 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작한다. 최선의 경우 O(N)의 시간 복잡도를 가진다.

※ 퀵 정렬과 비교했을 때, 보통은 삽입 정렬이 비효율적이나 '정렬이 거의 되어 있는 상황'에서는 퀵 정렬 알고리즘보다 더 강력하다! (=효율적이다.)

최선의 경우

- 비교 횟수
	이동 없이 1번의 비교만 이루어진다.
	외부 루프: (n-1)번

Best T(n) = O(n)

최악의 경우(입력 자료가 역순일 경우)

- 비교 횟수
	외부 루프 안의 각 반복마다 i번의 비교 수행
	외부 루프: (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)
- 교환 횟수
	외부 루프의 각 단계마다 (i+2)번의 이동 발생
	n(n-1)/2 + 2(n-1) = (n^2+3n-4)/2 = O(n^2)

Worst T(n) = O(n^2

참고문헌

https://velog.io/@kimdukbae/%EC%A0%95%EB%A0%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Sorting-Algorithm
https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
https://yabmoons.tistory.com/250