1. 버블 정렬

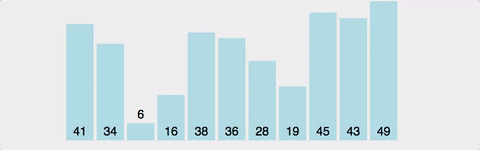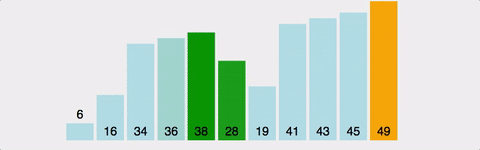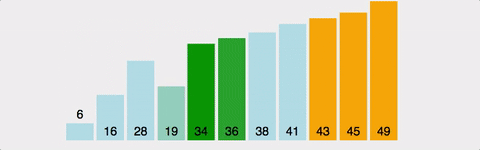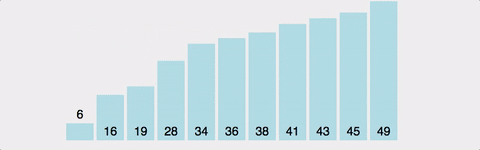
Bubble Sort는 Selection Sort와 유사한 알고리즘으로 서로 인접한 두 원소의 대소를 비교하고, 조건에 맞지 않다면 자리를 교환하며 정렬하는 알고리즘 이다.

이름의 유래로는 정렬 과정에서 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어졌다고 한다.

2. 버블 정렬 장단점

장점

• 일단 구현이 쉽다. Bubble정렬은 인접한 값만 계속해서 비교하면 되는 방식으로 굉장히 구현이 쉬운 편이다.

• 코드 자체가 직관적이다.

단점

• 굉장히 비효율적이다. 최악이든 최선이든 O(N^2) 이라는 시간복잡도를 갖기 때문에 사실 알고리즘에서 효율적인

  정렬방법으로 사용되지는 않는다.

3. 버블 정렬 구현

구현

일반적인 구현

# 버블 정렬의 범용성을 높이기 위해 함수로 만듬
def bubbleSort(arr):
    n = len(arr) # 배열의 크기를 측정

    # 배열의 크기만큼 반복
    for i in range(n):
        
        # 배열의 총 크기에서 i의 값과 1을 뺀 만큼 반복
        for j in range(0, n - i - 1):
            
            # 만약 현재 인덱스의 값이 다음 인덱스의 값보다 클경우 실행
            if arr[j] > arr[j + 1]: 
                arr[j], arr[j + 1] = arr[j + 1], arr[j] # 서로 위치를 변환

# 예시 배열
arr = [64, 34, 25, 12, 57, 93, 1, 123]

bubbleSort(arr)

최적화

• 이전 패스에서 앞뒤 자리 비교(swap)이 한 번도 일어나지 않았다면 정렬되지 않는 값이 하나도 없었다고 간주할 수 있습니다. 따라서 이럴 경우, 이후 패스를 수행하지 않아도 됩니다.

def bubble_sort(arr):
    for i in range(len(arr) - 1, 0, -1):
        swapped = False
        for j in range(i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swapped = True
        if not swapped:
            break

추가적인 최적화

• 이전 패스에서 앞뒤 자리 비교(swap)가 있었는지 여부를 체크하는 대신 마지막으로 앞뒤 자리 비교가 있었던 index를 기억해두면 다음 패스에서는 그 자리 전까지만 정렬해도 됩니다. 따라서 한 칸씩 정렬 범위를 줄여나가는 대신 한번에 여러 칸씩 정렬 범위를 줄여나갈 수 있습니다.

def bubble_sort(arr):
    end = len(arr) - 1
    while end > 0:
        last_swap = 0
        for i in range(end):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
                last_swap = i
        end = last_swap

시간복잡도 및 공간 복잡도

O(N^2)의 시간 복잡도를 가집니다

• 시간 복잡도는 우선 루프문을 통해 맨 뒤부터 맨 앞까지 모든 인덱스에 접근해야 하기 때문에 기본적으로 O(N)을 시간을 소모하며, 하나의 루프에서는 인접한 값들의 대소 비교 및 자리 교대를 위해서 O(N)을 시간이 필요하게 됩니다.
  따라서 거품 정렬은 총 O(N^2)의 시간 복잡도를 가지는 정렬 알고리즘입니다.
• 버블 정렬은 부분적으로 정렬되어 있는 배열에 대해서는 최적화를 통해서 성능을 대폭 개선할 수 있으며, 완전히 정렬되어 있는 배열이 들어올 경우, O(N)까지도 시간 복잡도를 향상시킬 수 있습니다.

O(1)의 공간 복잡도를 가집니다.

• 거품 정렬은 별도의 추가 공간을 사용하지 않고 주어진 배열이 차지하고 있는 공간 내에서 값들의 위치만 바꾸기 때문에 O(1)의 공간 복잡도를 가집니다.

참고문헌

https://velog.io/@gillog/%EB%B2%84%EB%B8%94-%EC%A0%95%EB%A0%ACBubble-Sort
https://yabmoons.tistory.com/250
https://www.daleseo.com/sort-bubble/