[DIP] 아핀변환(Affine transform)

Affine Transformation (아핀 변환): 아핀 변환은 원점을 보존하지 않는 선형 변환과 이동 변환의 결합입니다. 이러한 변환은 원래 이미지의 병렬성을 유지하면서
이미지를 확대/축소 (scaling), 회전 (rotation), 전단 (shearing),
그리고 이동 (translation) 등이 포함된다.
아핀 변환의 한 가지 중요한 특징은 변환 후에도 직선의 '직선성'이 유지된다는 것인데.

지금까지 들은 말로는 이게 도대체 무슨 소리인지 잘 이해가 안가지만,
즉 아핀변화에서 가능한 것들은 다음과 같다.

영상 확대/축소하기
영상 이동 하기
영상 평행 사변형으로 만들기
영상 회전하기

아핀변환을 진행하기 위해선 조건이 필요한데

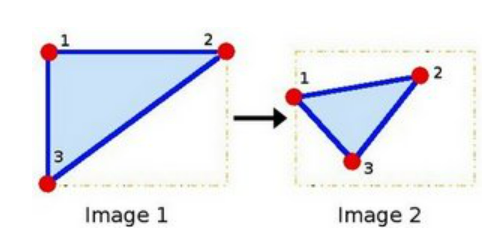
2차원 공간에서 아핀 변환을 완전히 표현하려면 최소 세 개의 불공선점(non-collinear points, 한 직선 위에 있지 않은 점들)이 필요하다. 이 세 점은 원본 이미지에서의 위치와 변환된 이미지에서의 위치를 결정한다.

왜 한 직선위에 있지 않냐 하면, 한 선위에 점이 세개가 있다면 그건 1차원이기 때문에 영상으로 만들 수 없다.

아핀 변환은 수학적으로 다음과 같은 2x3 행렬로 표현할 수 있는데
행렬로 표현할 때, 아핀 변환은 아래와 같이 나타낼 수 있다:
$\begin{bmatrix}a & b & e \\c & d & f \\ \end{bmatrix}$

여기서,

a, b, c, d는 선형 변환에 해당하며, 이미지의 확대, 축소, 회전, 전단 등을 담당한다.
e, f는 이동 변환에 해당하며, 이미지의 위치를 이동시킨다.
각 변환은 다음과 같다:

확대/축소: a와 d 값에 의해 결정된다. a 값이 x축 방향의 확대/축소를, d 값이 y축 방향의 확대/축소를 제어합니다.

회전: a, b, c, d 값에 의해 결정된다. a와 d는 코사인 값을, b와 c는 사인 값을 갖는 회전 행렬을 형성한다.

전단: b와 c 값에 의해 결정된다. b 값은 y축 방향으로의 전단 변환을, c 값은 x축 방향으로의 전단 변환을 제어한다.

이동: e와 f 값에 의해 결정된다. e 값은 x축 방향으로의 이동을, f 값은 y축 방향으로의 이동을 제어한다.

아핀 변환을 완전히 표현하려면, 위에서 설명한 성분들을 모두 제어할 수 있어야 하므로, 각 점의 x, y 좌표를 결정하는 세 개의 점이 필요하다.

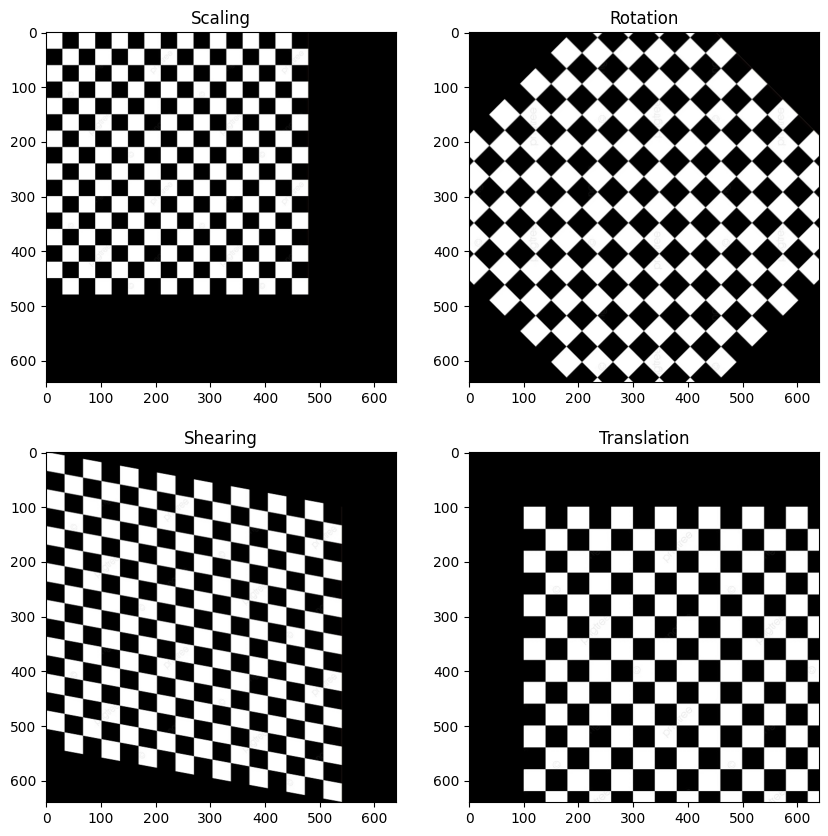
보다 직관적으로 알 수 있게 파이썬으로 아핀 변환의 네가지 기능에 대해 알아보자.

사용할 이미지는 다음과 같다.

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 이미지 로드
img = cv2.imread('../img4.jpg') #이미지 path 설정
rows, cols, ch = img.shape
# 변환 점 설정
pts1 = np.float32([[0, 0], [640, 0], [0, 640]])

# 확대/축소 변환
pts2_scaling = np.float32([[0, 0], [480, 0], [0, 480]])  # 약 0.75배 축소
matrix_scaling = cv2.getAffineTransform(pts1, pts2_scaling)
result_scaling = cv2.warpAffine(img, matrix_scaling, (cols, rows))

# 회전 변환
angle = 45  # 45도 회전
matrix_rotation = cv2.getRotationMatrix2D((cols/2, rows/2), angle, 1)
result_rotation = cv2.warpAffine(img, matrix_rotation, (cols, rows))

# 전단 변환
pts2_shearing = np.float32([[0, 0], [540, 100], [0, 540]])  # x축 방향으로 약간의 전단 변환

matrix_shearing = cv2.getAffineTransform(pts1, pts2_shearing)
result_shearing = cv2.warpAffine(img, matrix_shearing, (cols, rows))

# 이동 변환
pts2_translation = np.float32([[100, 100], [740, 100], [100, 740]])  # 오른쪽 아래로 100픽셀 이동
matrix_translation = cv2.getAffineTransform(pts1, pts2_translation)
result_translation = cv2.warpAffine(img, matrix_translation, (cols, rows))

# 결과 이미지 그리기
plt.figure(figsize=(10, 10))

plt.subplot(221), plt.imshow(result_scaling), plt.title('Scaling')
plt.subplot(222), plt.imshow(result_rotation), plt.title('Rotation')
plt.subplot(223), plt.imshow(result_shearing), plt.title('Shearing')
plt.subplot(224), plt.imshow(result_translation), plt.title('Translation')

plt.show()

결과: