
강의 출처
강의 목표
- 이 과정은 자료구조와 알고리즘의 심화편 이기 때문에, 기본편 학습이 필요.
- 즉 , <비선형 자료구조와 알고리즘> 을 배울 예정
🚨선형 자료구조와 알고리즘 보다 복잡하고 어렵다 ( 배열, 연결리스트, 스택, 큐, 재귀함수에 대해 알고 있어야 함 )
그래서 금주 주말에 추가로 해당 기본 개념들 공부 할 예정 😁
P-NP란?
- 알고리즘을 공부하다 보면, P-NP라는 개념에 대해 접하게 될 것.
- 이번강의에서는 "P문제"를 다룰 예정, P문제가 아닌 경우 어떤 문제에 포함되는지 추가 설명함.
빅 오 (Big-O)
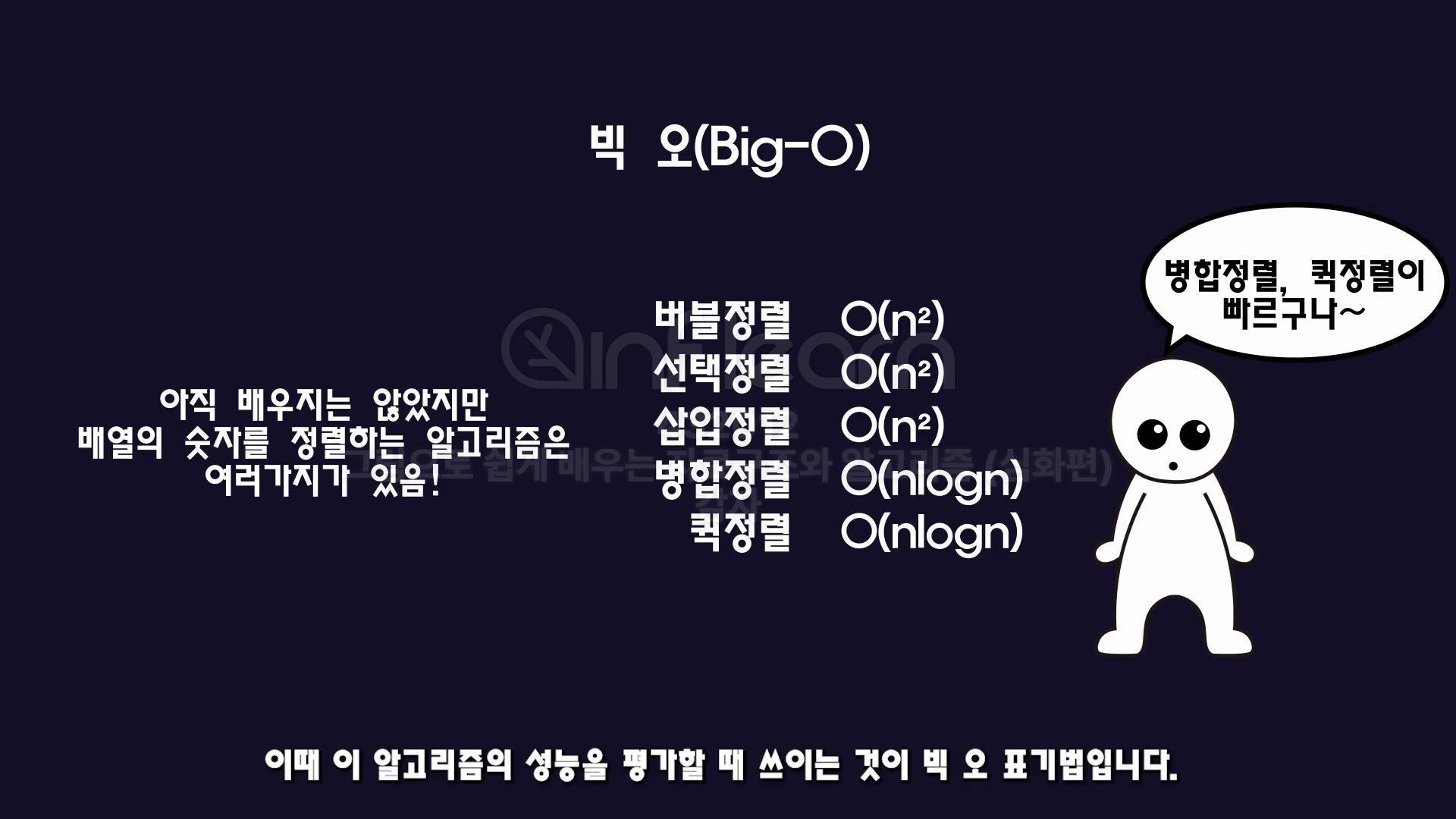
- 알고리즘의 성능을 평가하는데, "빅 오 " 표기법을 씀
- 예시) 배열의 숫자를 정렬하는 알고리즘의 종류 👉🏻 버블정렬,선택정렬,삽입정렬,병합정렬,퀵정렬
어떤 문제를 해결할 때 사용되는 방법 = 알고리즘 은 여러가지가 있음
P-NP
- 반면 P-NP문제는 어떤 문제가 주어졌을때
- 쉬운 문제인지 아닌지, 해결이 가능한지 아닌지 판단하는 척도가 된다.
- 이 P-NP문제를 판단하기 전에 "결정 문제"를 익혀야 한다.
결정 문제 ( Decision Problem )
- 어떤 문제에 대해 (YES/NO) 로 대답할 수 있는 문제.
- 예 ) 10%2 == 0 인가? 👉🏻 YES/NO로 대답 가능함 👉🏻 결정문제
최적화 문제 ( Optimization Problem)
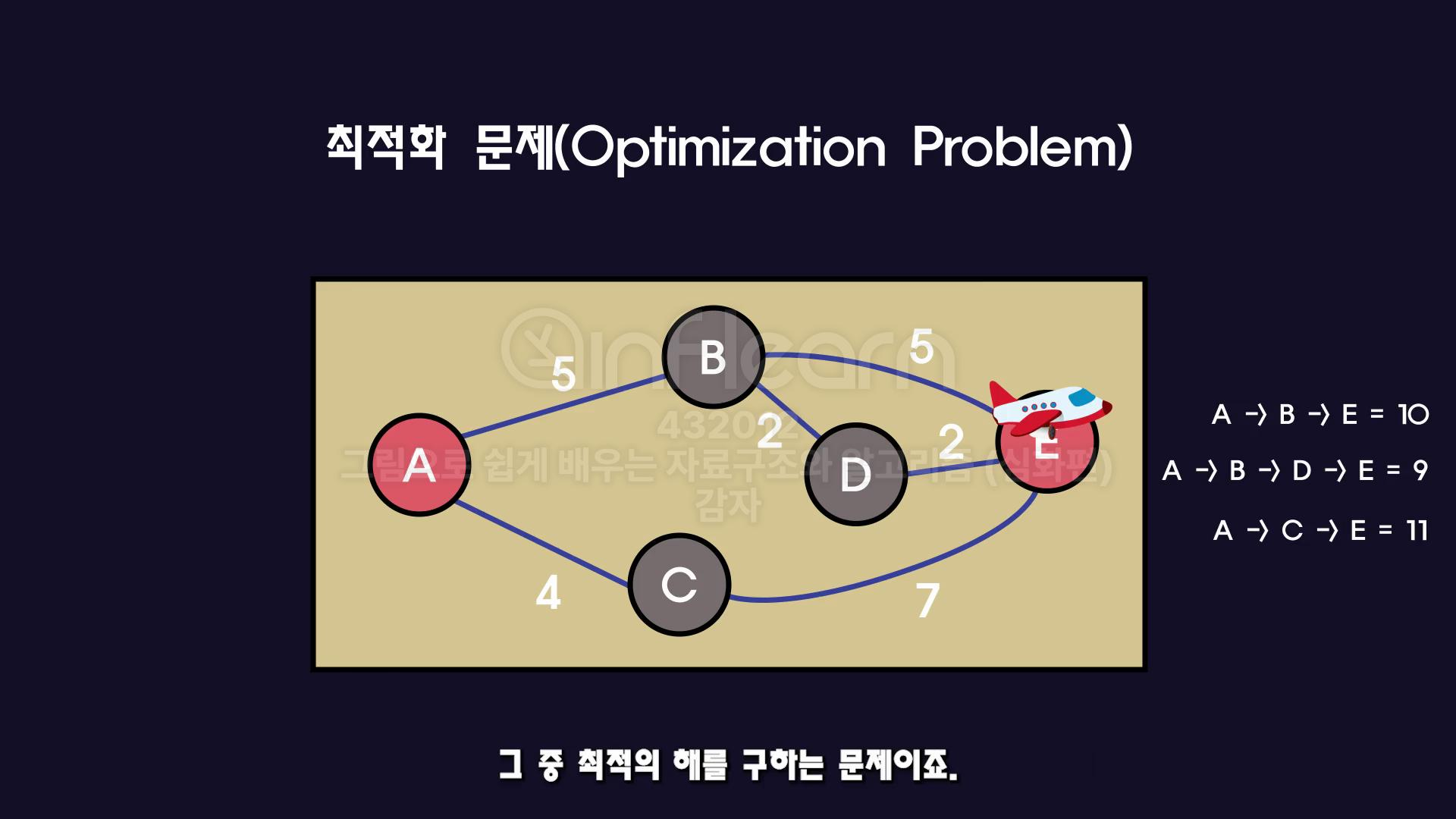
- 어떤 상황이 주어지고, 거기서 최적의 해답을 찾으라는 문제.
- 예 ) 이미지 처럼, A경로에서 시작해서 E지점까지 가장 짧은 경로 구해야함.
- YES/NO 대답 못하고, 여러 경우의수를 계산하여 최적의 해를 구하는 문제를 "최적화문제"라고 함.
그러나 대부분의 최적화 문제는 "결정문제"로 바꿀 수 있음!
- 예를들면, A지점에서 E지점까지 경로 중 10보다 작은 경로가 존재하는가?
- 최적화 문제에서 특수 조건을 추가하여 , 결정문제로 바꾼 상태.
- 답변은 YES/NO대답 가능함. - 이제 P-NP문제에 대해 알아보자.
P문제
- 결정론적 튜링머신으로 다항시간에 문제해결이 가능한 문제
1️⃣ 결정론적 튜링 머신
- 현재상태 👉🏻 다음상태로 이동 될때, 다음 상태가 유일하게 결정되는 머신.
- 다음의 상태가 결정되니깐, 문제를 차근차근 해결해 나가기 때문에, 일방향으로 해결함.

if-else 문은 결정론적 튜링머신 방식?
if문이 참 👉🏻 if문이 수행
if문이 거짓 👉🏻 else문이 수행되는 유일한 상태가 된다.
컴퓨터 자체가 결정론적 튜링머신!
2️⃣다항시간 ( Poynomial time )
- 문제를 해결하는 시간 👉🏻 다항식으로 표현할 수 있는 것
x² - 2x + 3- 다항식이란? : x 값에 대해 여러 항이 존재하는 식을 말한다.
- 이 다항식을 빅오 표기법으로 표현하면?
O(x²)- 만약, 어떤 알고리즘의 성능이 O(x²) 이라면? 다항시간내에 답을 구할 수 있는 알고리즘 이라는 것.
- 차수가 들어나더라도 , 이 알고리즘은 다항 시간내에 해결할 수 있는 알고리즘.
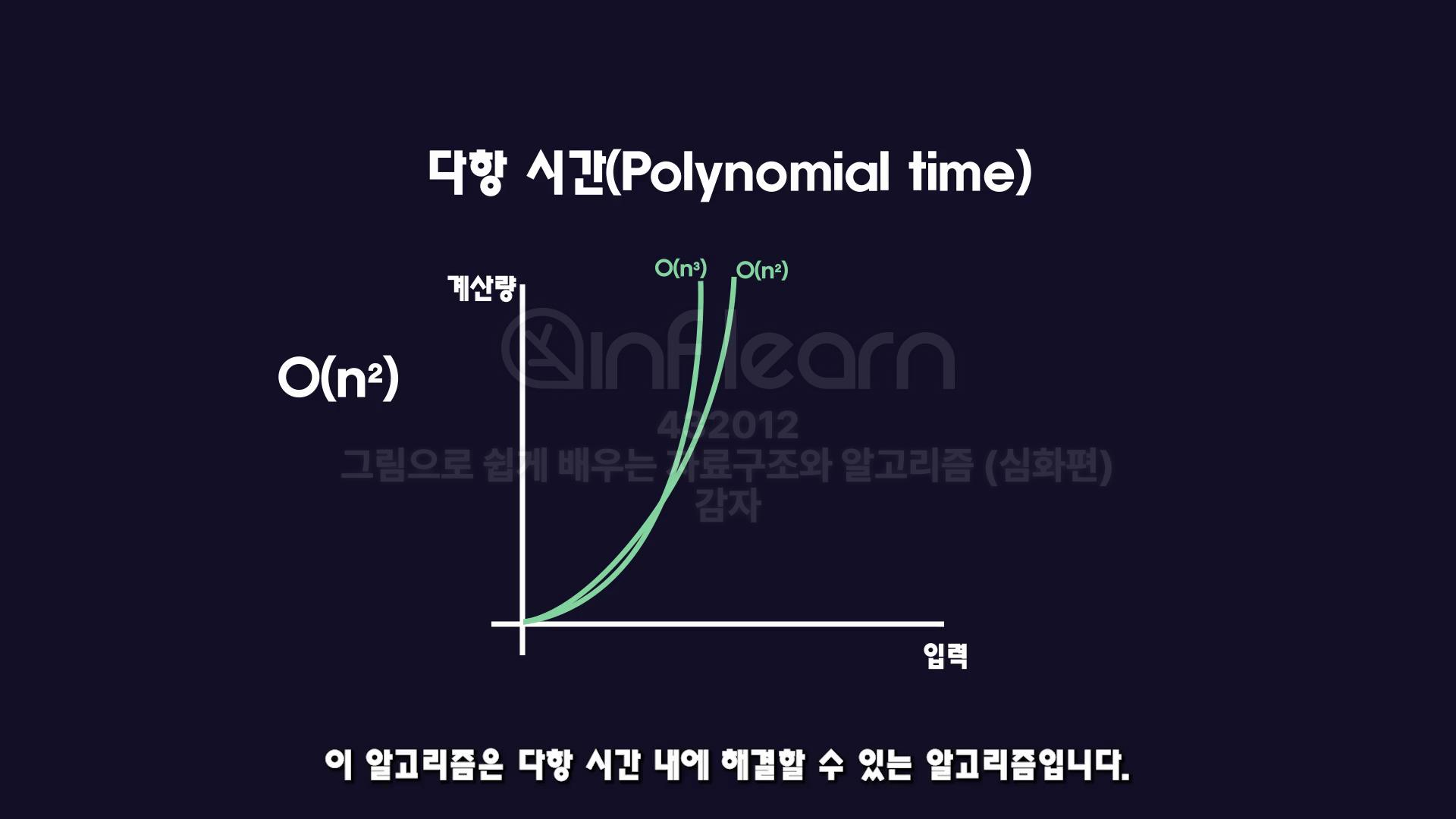
- 상수시간인 O(1) 과 로그시간인 O(logn) 은 모두 다항시간 보다 더 작으므로, 다항시간내에 답을 구할 수 있음.
즉, 상수시간, 로그시간, 다항시간이 P문제! 우리가 대부분 접하는 것들이 P문제임.
정렬 (Sorting)
- 대표적인 P문제
- 정렬 문제를 가장 쉽게 해결하는 알고리즘은 " 버블 정렬 알고리즘 "
버블 정렬 알고리즘 동작방법
- 만약 [3,4,1,2] 배열을 👉🏻 [1,2,3,4] 오른차순으로 정렬 하려면
- 첫번째 원소인 (3) 과 두번째 원소(4)를 비교해서 "3은 4보다 큰가?" 라는 결정문제가 주어짐
- YES/NO대답 👉🏻 NO라서 아무런 반응 없다
- 두번째 원소 (4)와 세번째 원소(1)를 비교하여 "4는 1보다 큰가?"
- YES대답 👉🏻 그러면 서로 자리 바꾸기 👉🏻 [3,1,4,2]
- 세번째 원소(4)와 네번째 원소(2) 비교하여 " 4는 2보다 큰가? "
- YES대답 👉🏻 자리 바꾸기 👉🏻 [3,1,2,4]
- 다시 돌아와서 3이 자기 자리 찾는거 반복해서 오름차순으로 [1,2,3,4] 로 자리 배치하게 정렬들어감.
- 현재 배열의 길이는 4개라서,
- 4의자리가 찾아가기 위해 3번 숫자를 비교했음
- 3의 자리가 본인 자리 찾아가기 까지 2번 비교
- 2의 자리는 1번 비교함
- 이걸 식으로 표현하면, 등차수열의 합공식으로 n(n-1)/2로 표현
- 이걸 빅 오 표현법으로 표현하면 O(n²) 즉 다항시간 , 즉 P문제로 구분된다.
"A는B보다 큰가?" 라는 결정문제를 반복 👉🏻 결정론적 튜링 머신으로 다항 시간 내에 정렬을 완료함.
NP문제란?
- 결정 문제가 주어졌을 때, 비 결정론적 튜링 머신을 사용해 다항 시간 내에 답을 구할 수 있는 문제.
✳️비결정론적 튜링 머신
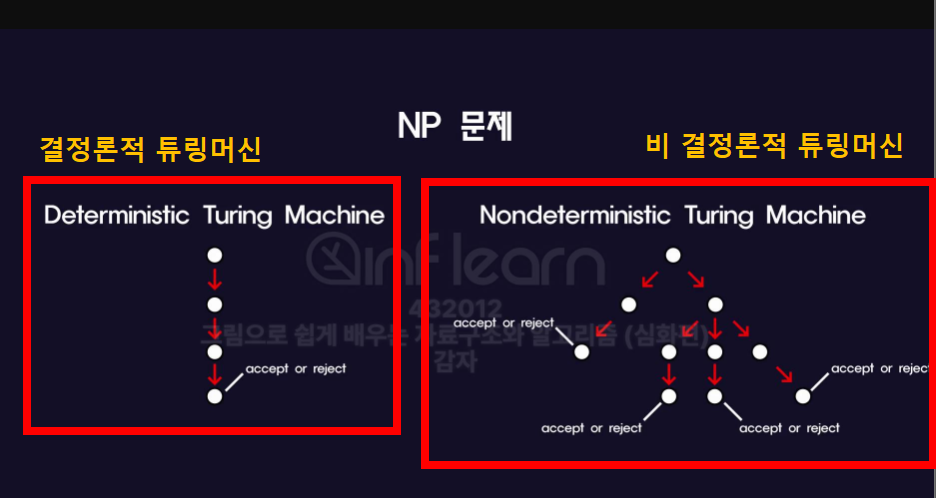
- 현재상태 👉🏻 다음상태 이동할 때, 다음 상태의 갯수가 여러개인 머신.
- 현실 세계에서 볼 수 없음 ( 상상으로 있다고 "가정" 함 )
- 이해하기 어려우니, 동일한 결정문제에 결정론적 튜링머신 VS 비 결정론적 튜링머신이 해결하는 방법의 차이점에 대해 알아보자.
NP문제에 대한 결정론적 튜링 머신 vs 비 결정론 튜링 머신
결정론적 튜링 머신( NP문제 해결 못함 )
: NP문제 해결에 있어서, 결정론적 튜링 머신은 지수 시간으로 답을 구해야하고, 운의 요소가 강함
- 경우의 수 가 엄청 많음. 해당 경로를 하나하나씩 직접 들어가서 결정문제에 대한 YES/NO답을 줄 수 있음.
- 결과론적으로 그러나 "힌트"가 주어질 때 다항시간내에 정답인지 아닌지 확인하는 것 가능함.
그러나, 답을 빨리 못찾아도 확인(=검증) 하는건 빠르다.
- 예) 이 경로A는 금고가 존재하는지?아닌지? 👉🏻 YES/NO대답 빠르게 가능
- 모든 P문제는 NP문제이기도 하다.
모든 P문제를 비 결정론적 튜링 머신을 사용해, 다항 시간 내에 답을 구할 수 있음.
NP-hard 문제
- 어떤 NP문제들이 있을 때, 이 모든 NP문제들을 다항 시간 내에 어떤 문제 A로 환원시킬 수 있다면, 그 문제 A 를 NP-hard문제라고 부름.
- 예시 NP문제는 아래 이미지 참조

- 문제 B,C,D를 확인해보면 문제A만 해결하면 자연스레 B,C,D도 해결이 가능함.
- 이런식으로 NP문제들(B,C,D)이 문제 A로 환원 될 수 있다고 얘기함.
- 환원된 A문제를 "NP-hard" 문제 라고 부른다.
NP-complete 문제

- NP-hard 문제에도 포함 되면서 NP문제에도 포함되는 문제.
- 두개의 차이점은 뭘까?
- NP-complete 는 문제 해결이 가능하다고 판별이 ⭕
- NP-hard 는 문제 해결이 가능한지,아닌지 판별이 ❌
마무리 하며
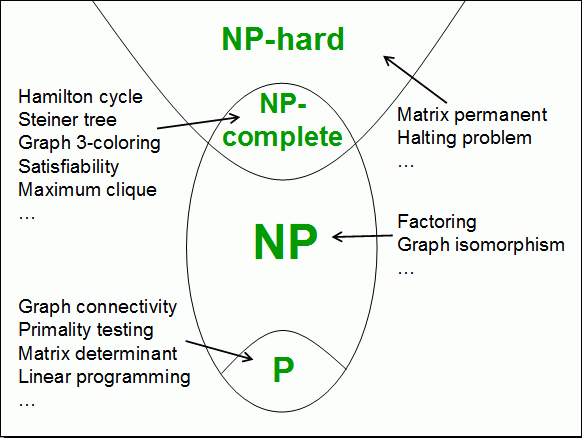
P vs NP
- P : 결정론적 튜링 머신으로 다항 시간내에 해결 ⭕ 쉬운문제
- NP : 비결정론적 튜링 머신으로 다항 시간내에 해결 ⭕ P보다 어려운 문제
- ✳️힌트가 주어지면 (YES/NO를) 결정론적 튜링 머신으로 다항 시간내에 확인 ⭕
NP-hard vs NP-complete
- hard : 어떤 NP문제들이 있을 때, 이 모든 NP문제들을 다항 시간 내 👉🏻 어떤 문제A로 환원시킬수 있으면 , 이 문제A를 hard문제라고 부름
- 그런데 이 hard문제를 해결할수 있는지 밝히지 못한 가장 어려운 문제 - comlete : NP-hard문제 이면서 NP인 문제
- 풀수 있는 문제 중에서 가장 어려운 문제
🤔P - NP 문제의 핵심 질문 "P = NP인가?"
- 다항 시간(Polynomial time)에 해결 가능한 문제(P) & 다항 시간에 검증 가능한 문제(NP)가
본질적으로 같은 클래스인지, 아니면 서로 다른 클래스인지
✳️만약 P = NP라면, NP 문제(예: 암호 해독, 최적화 문제)를 다항 시간에 해결할 수 있는 알고리즘이 존재한다는 뜻.
✳️반대로 P ≠ NP 라면, NP 문제 중 일부는 다항 시간에 해결 불가능하다는 뜻으로, 현재 대부분의 학자들이 이쪽을 지지하고, 우리가 방금까지 배워왔던 내용인 것.
