강의 출처

• 인프런 워밍업클럽 4기 - CS전공지식
• 인프런 강의 - 자료구조와 알고리즘

---

목차

1. 트리의 개념
2. 이진트리의 개념
3. 이진트리 구현

개요

• 비선형 자료구조와 알고리즘에 대해 알아볼 예정
• 선형 자료구조보다 복잡함
• 비선형 자료구조 중 가장 먼저 " 트리 " 라는 자료구조 파헤쳐보자.

---

1️⃣트리란?

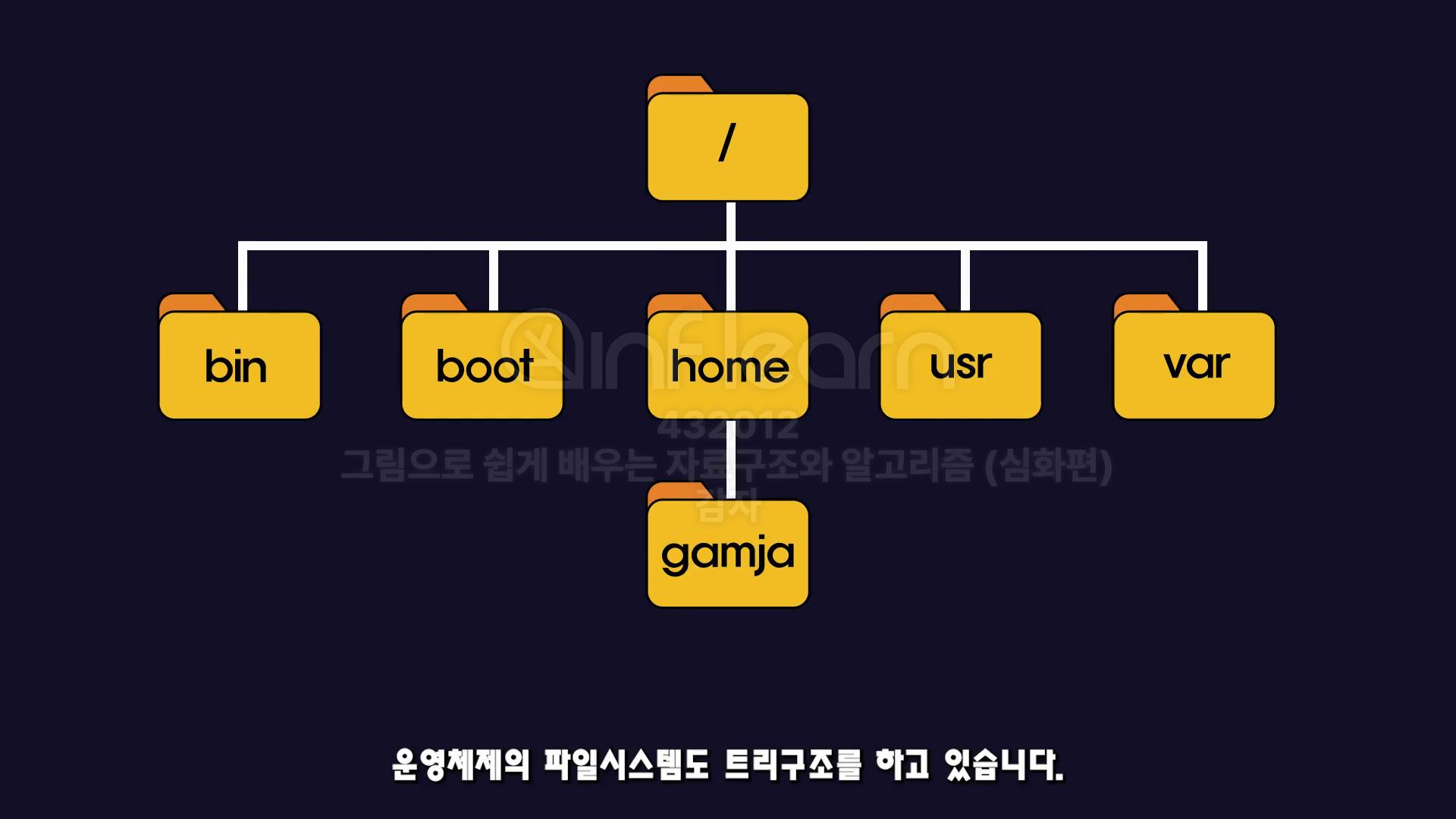
• 말그대로 나무 처럼 생겼음 ( ex.회사 조직도,운영체제의 파일시스템 )

  하나의 노드에서 여러가지의 나뭇가지로 가지치기 하며 내려가는것 = "계층구조"를 표현하기에 제격이다.

트리 구조 및 용어

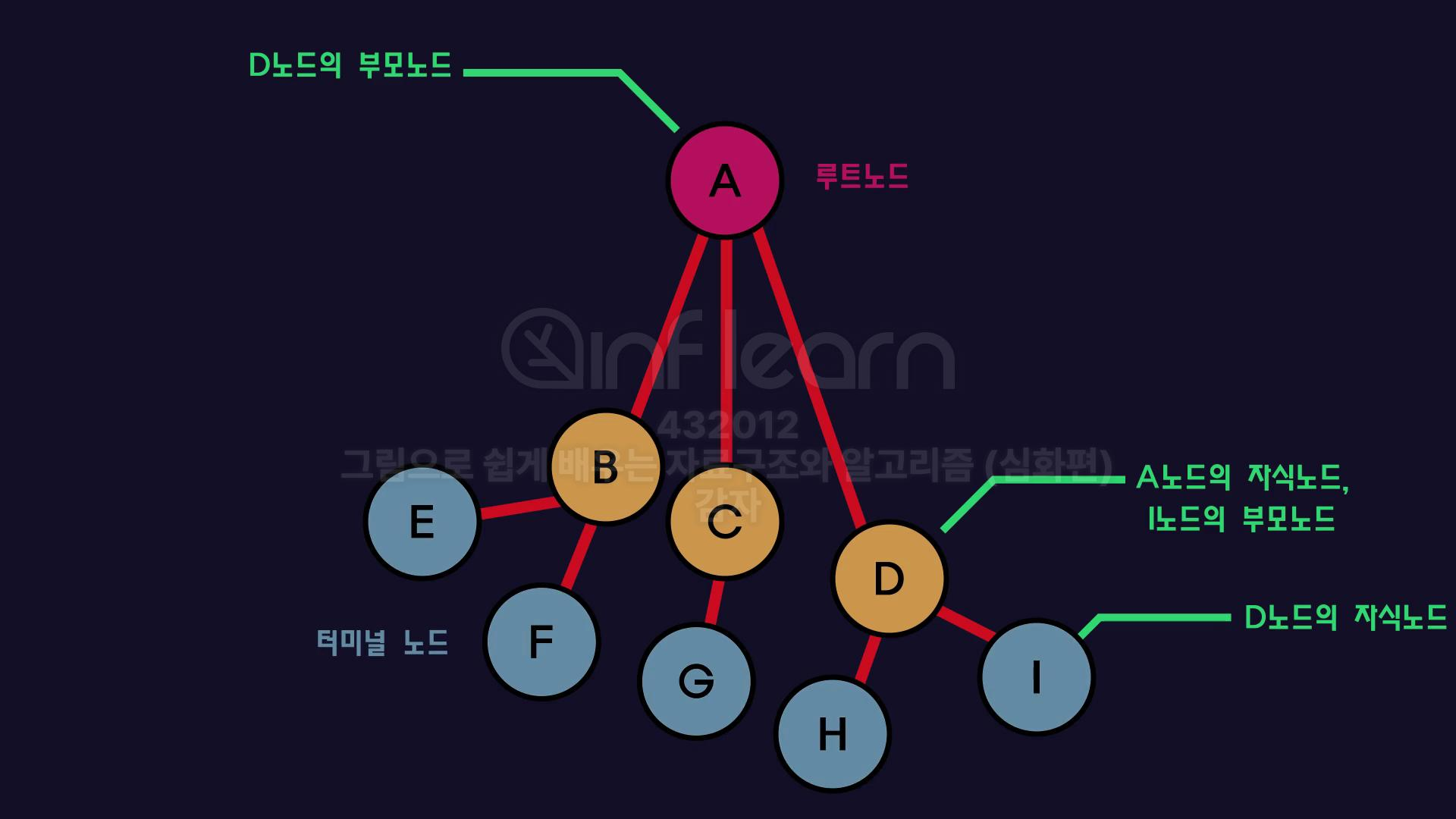
1. 노드 Node

• 데이터를 담는 가장 작은 단위(덩어리)

2. 엣지 Edge

• 각 노드를 연결하는 선

3. 루트노드 Root Node

• 트리노드에서 가장 최상위의 노드

4. 터미널 노드 Terminal Node

• 자식노드가 없는 부모노드

  참고로, 터미널노드는 루트노드만 있는 트리로 볼 수 있음

5. 인터널 노드 Internal Node

• 루트노드,터미널노드를 제외한 노드

6. 서브트리

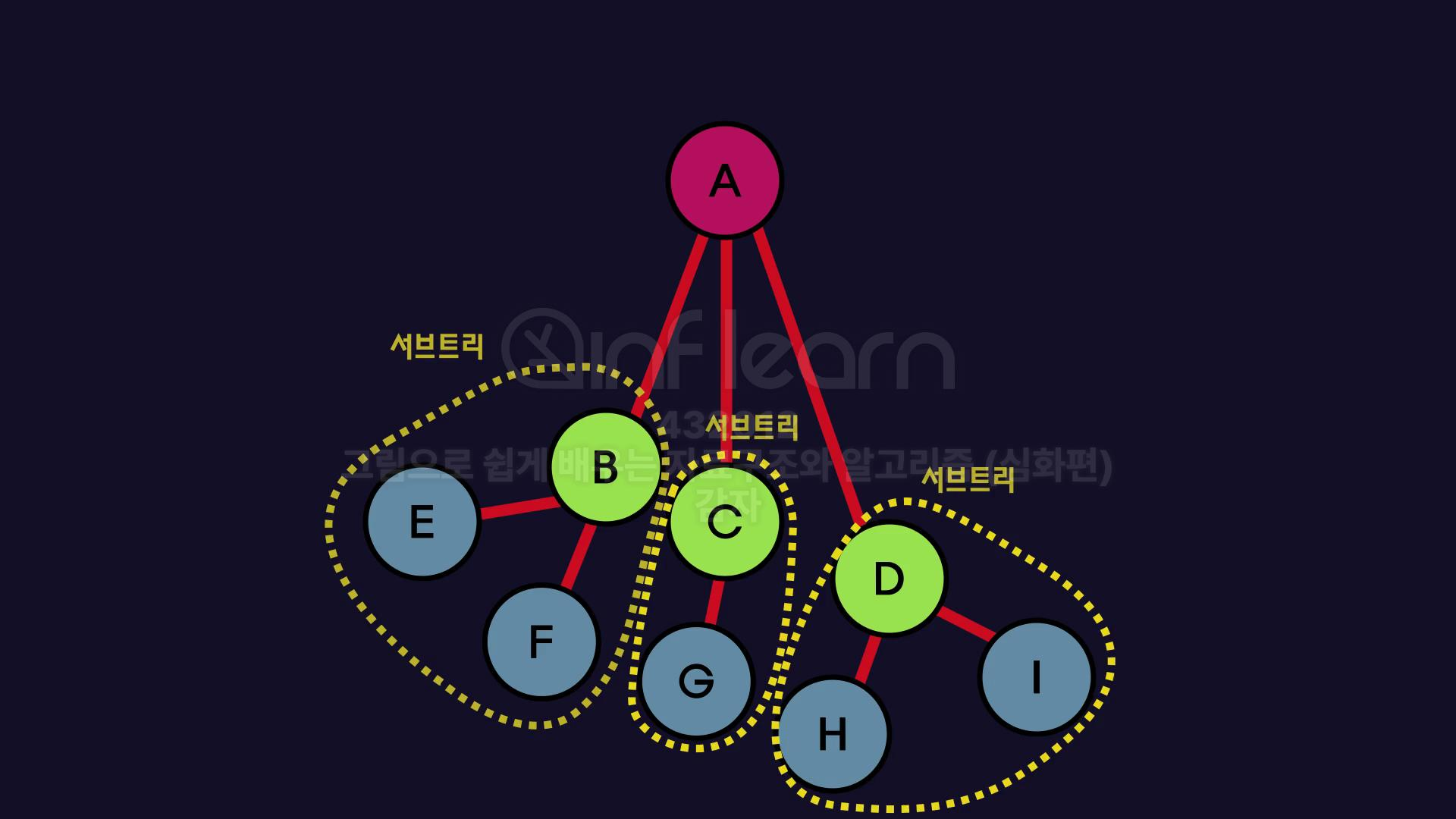
• 루트노드인 A인 입장에선, 3개의 서브트리가 연결된 구조

---

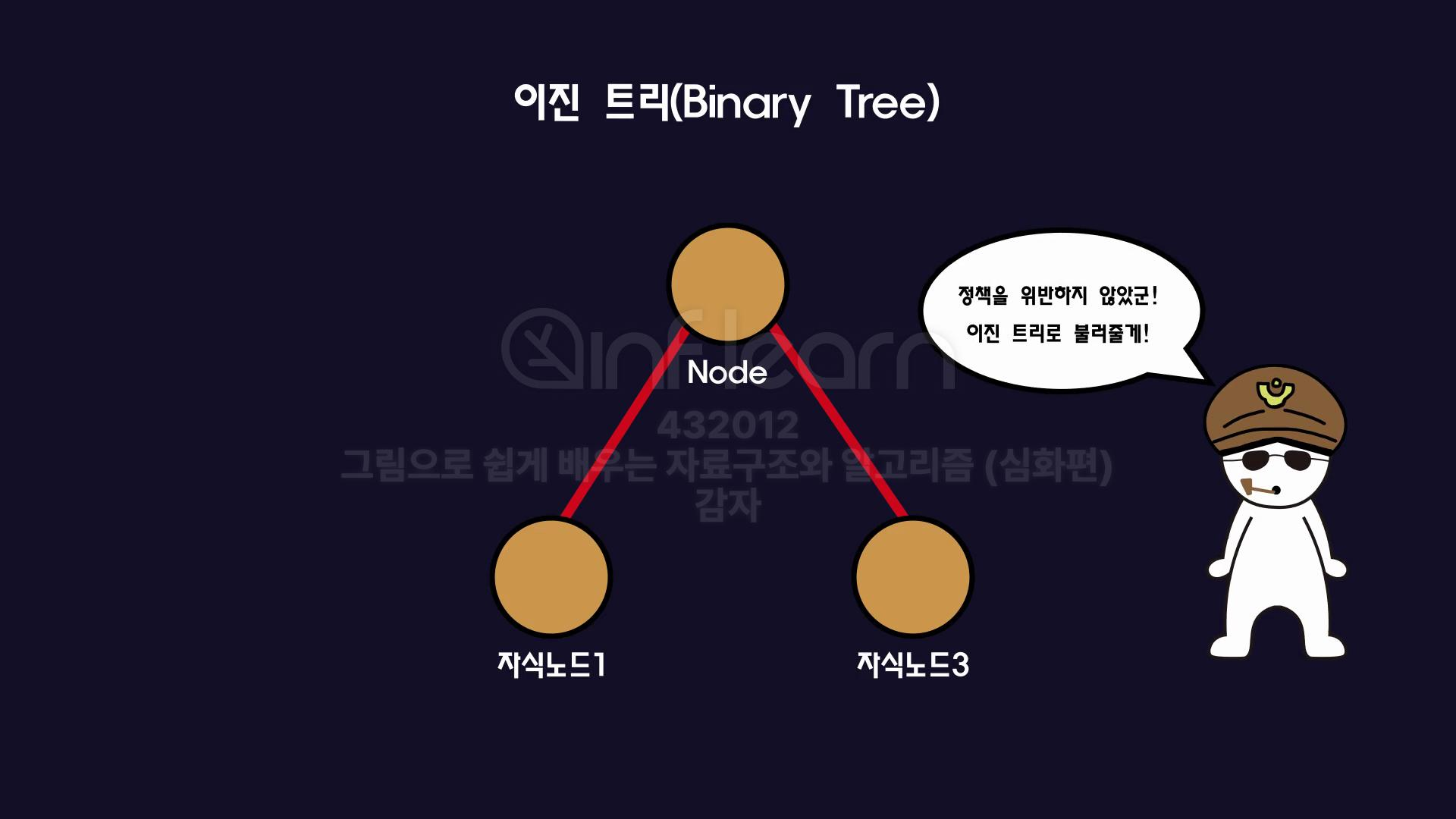
2️⃣이진트리란? (Binary Tree)

• Tree에서 어떤 규칙을 지켜야지 Binary Tree라고 불리운다.
• 그 규칙은 무엇일까?

  자식노드가 최대 "2개" 만 가져야지 이진트리이다.
  

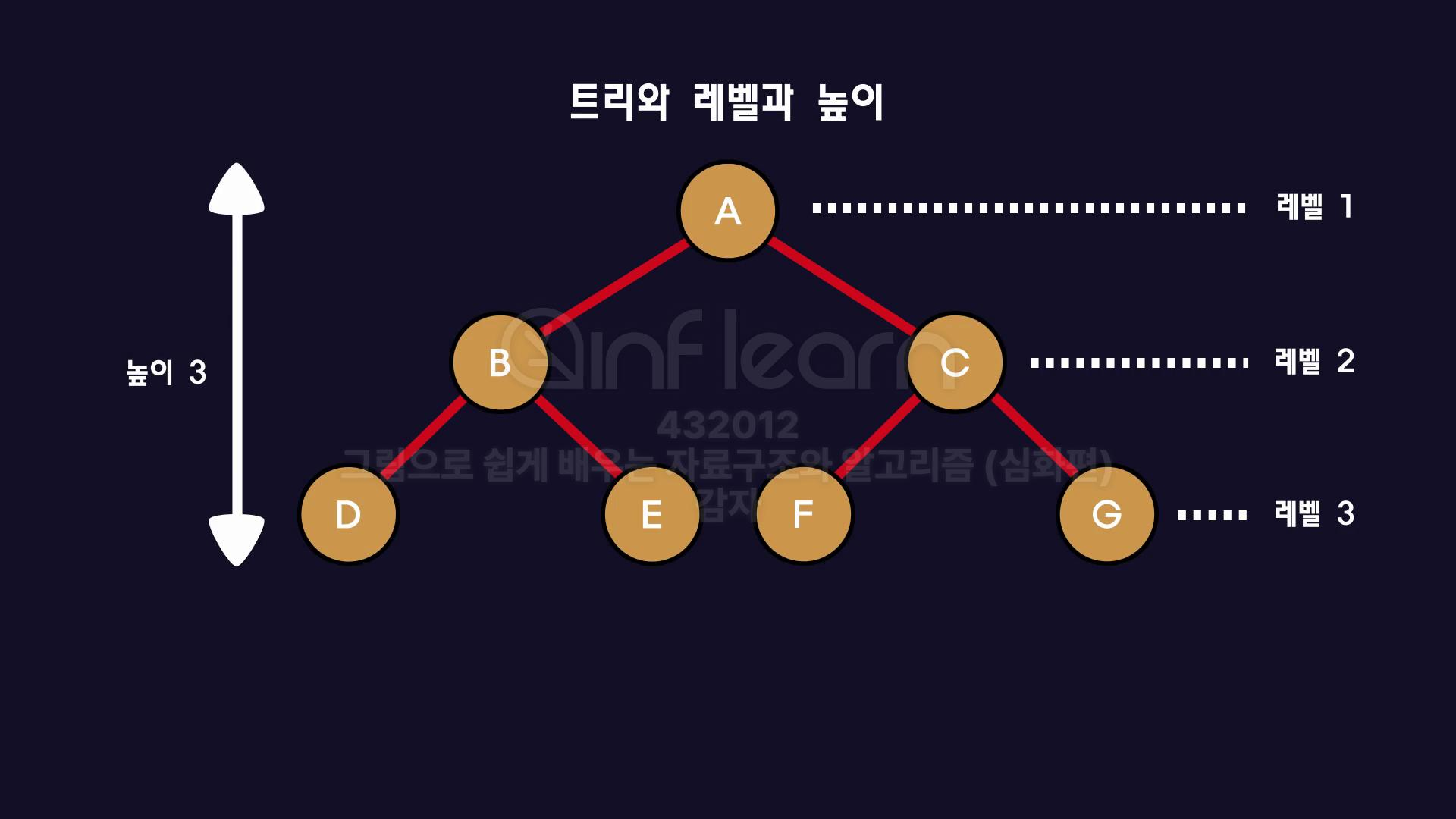
트리의 레벨과 높이

• 트리는 아래로 갈 수록 레벨이 높다.
• 이 레벨의 최대 단위를 "높이"라고 표현함 .
• 즉 레벨이 3이면, 이 트리의 높이도 3이다.
  

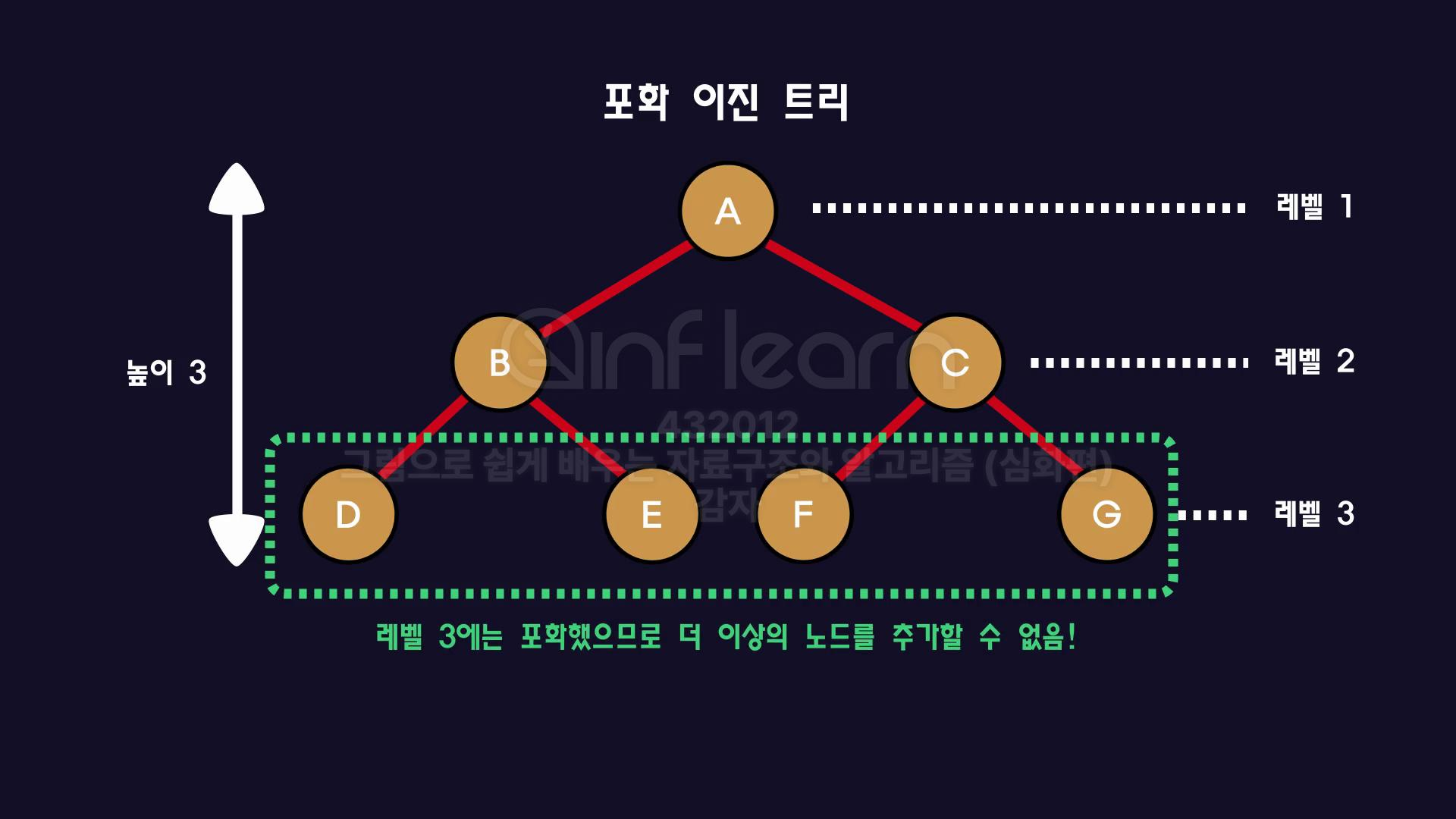
포화 이진 트리

• 트리의 최대 레벨에 있는 모든 터미널 노드가, 꽉 찬 트리

• 예 ) 트리 높이가 3이며, 레벨3에 있는 노드(=터미널노드)들이 꽉 차있으므로 노드 추가가 불가한 상태
  

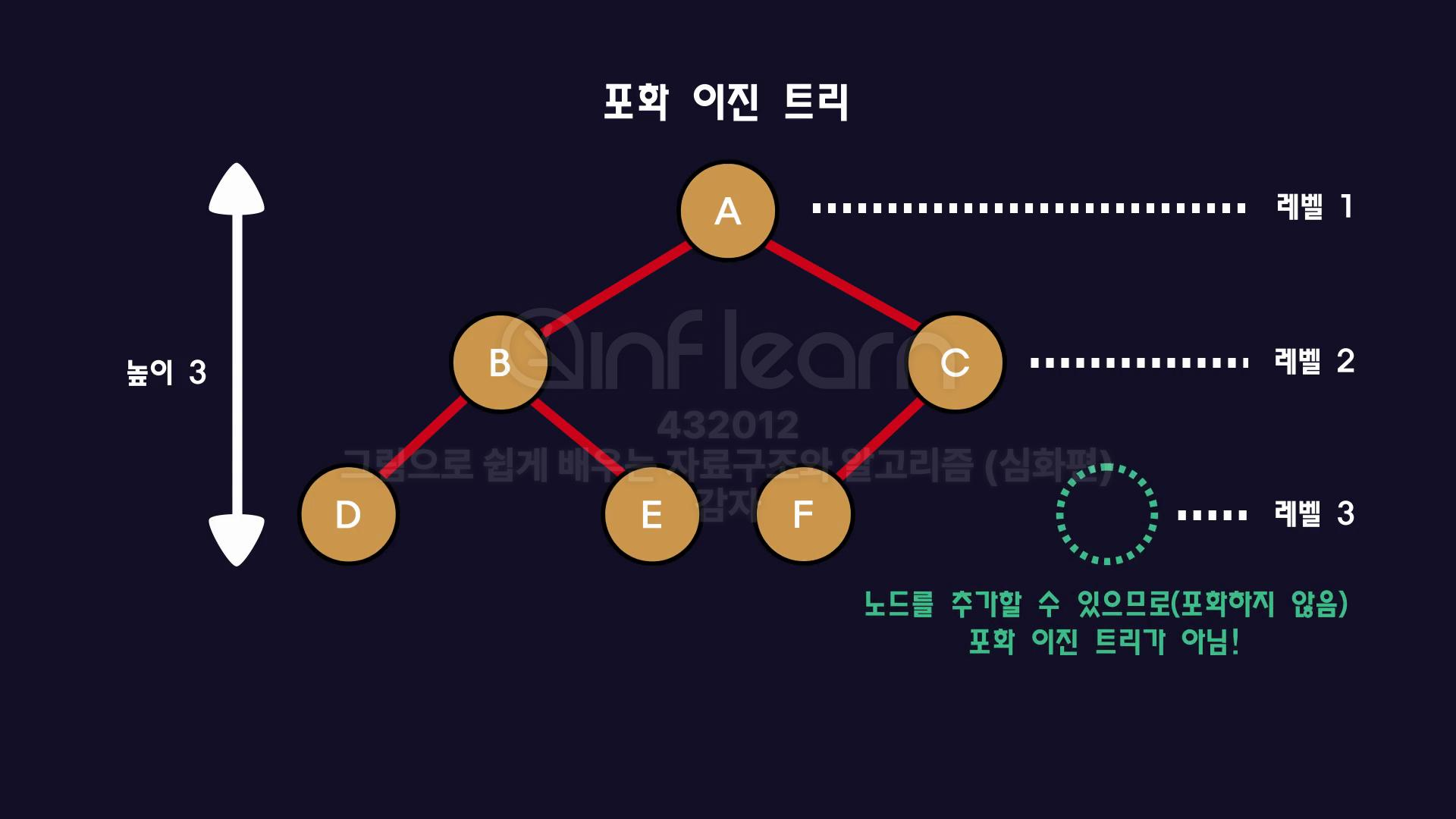
• 만약, 터미널노드가 꽉 차있지 않으면? 노드 추가 가능
  

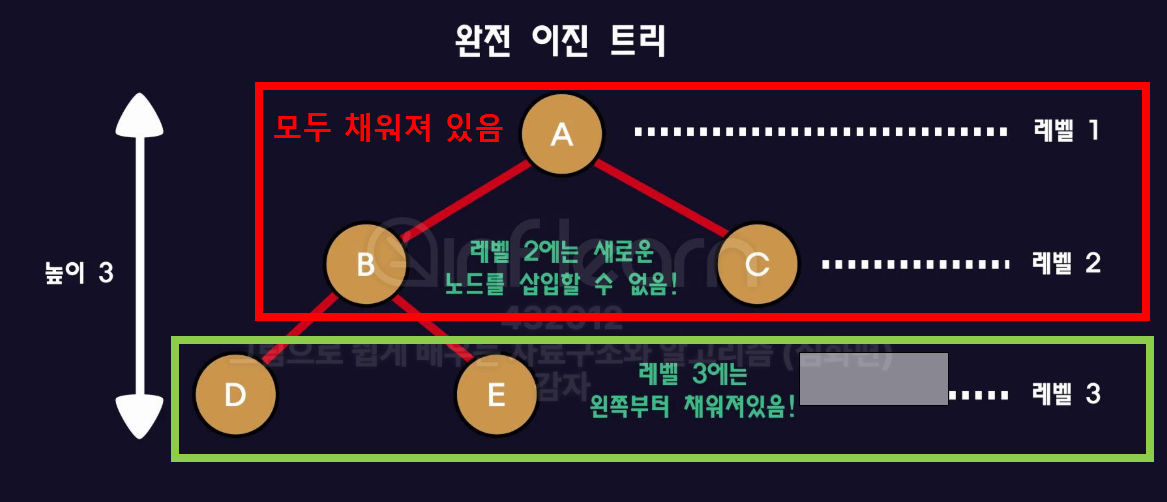
완전 이진 트리

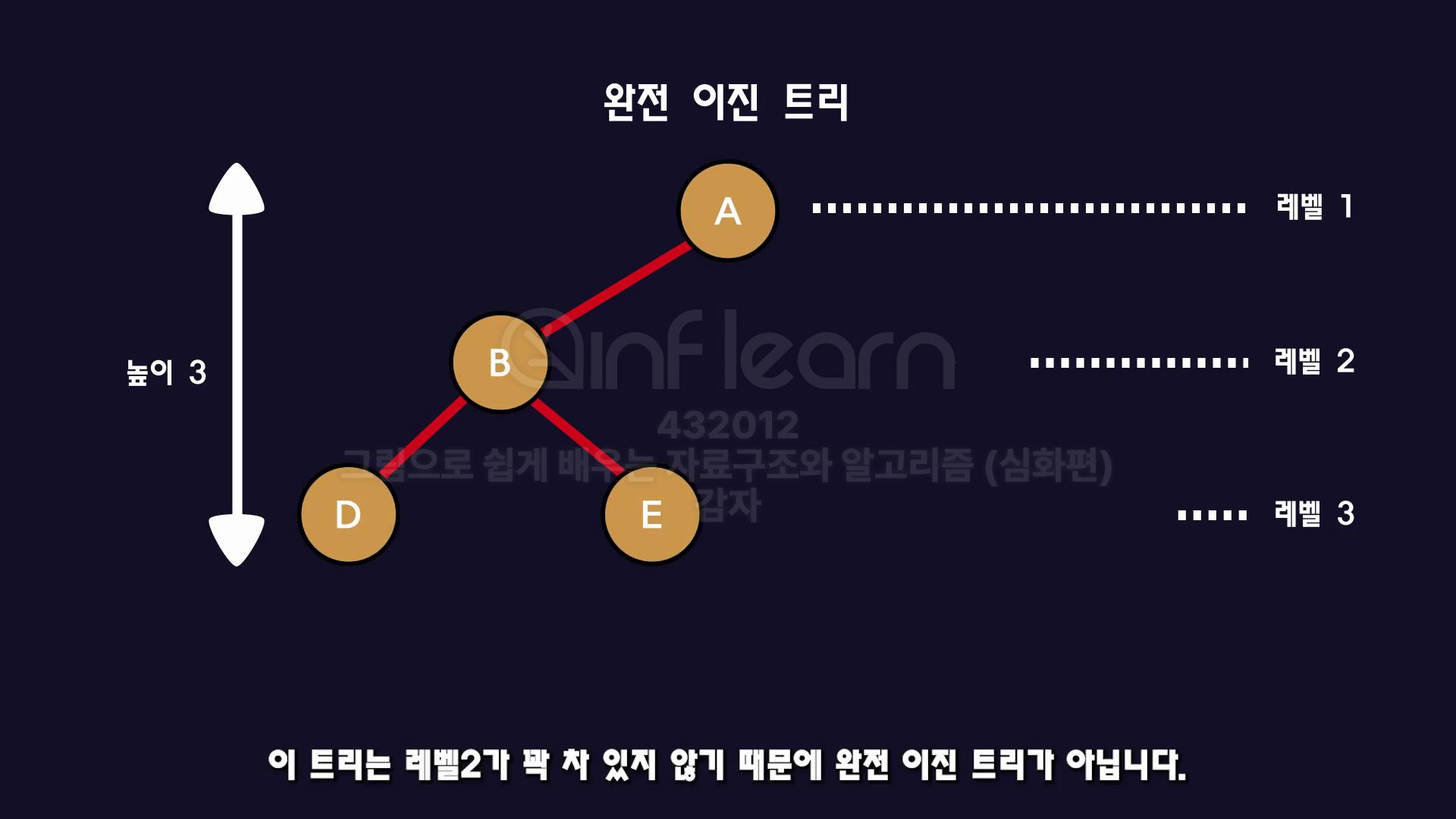
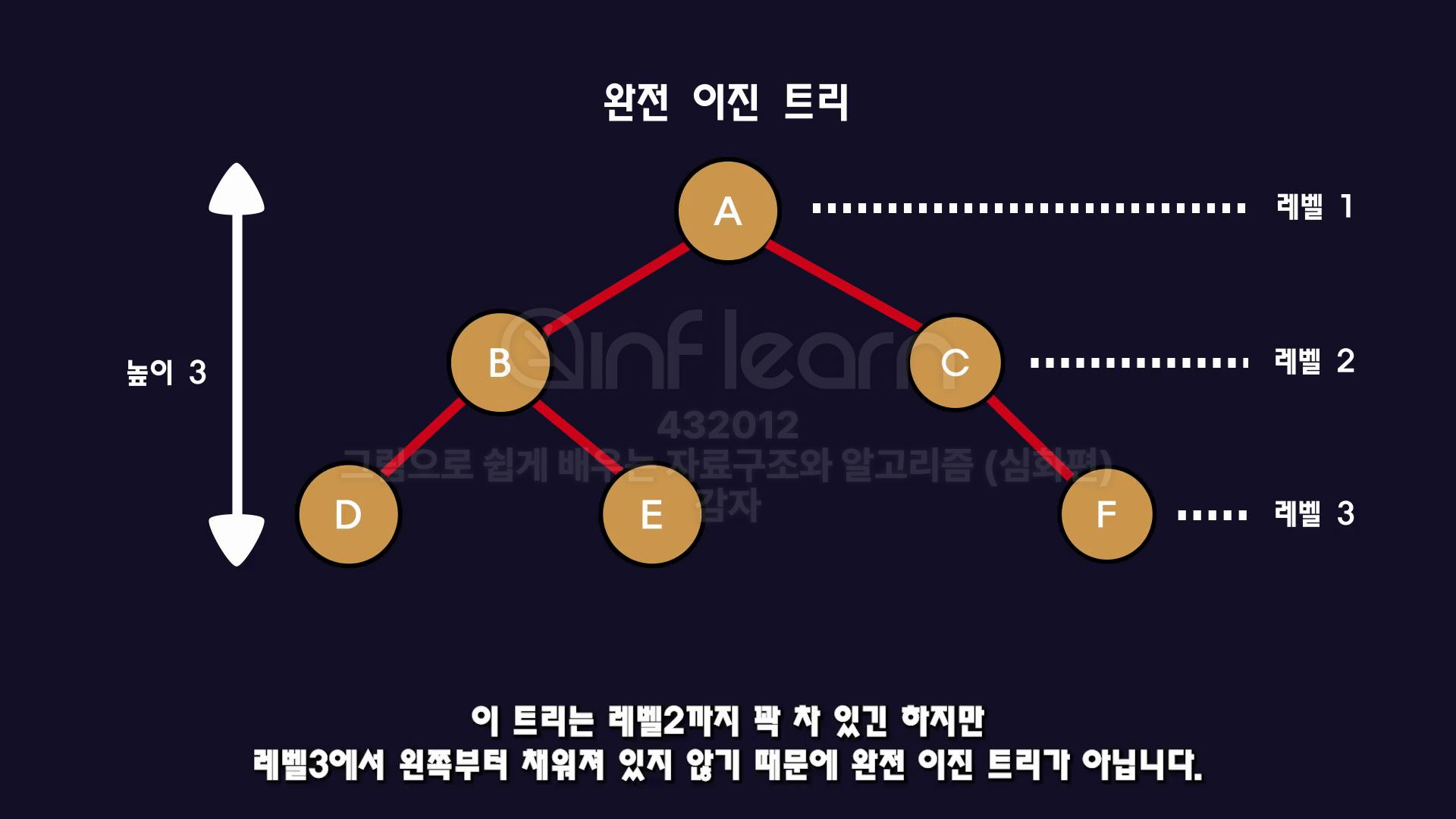
• 최대 레벨을 제외한 나머지 레벨에는 모두 채워져 있어야하고, 최대레벨의 노드들은 "왼쪽"부터 채워진 트리들을 말함.

질문, 이 트리는 "완전 이진 트리" 일까요?

답은 ❌ 레벨2 노드가 꽉 채워져 있지 않음

답은 ❌ 레벨2까지는 모두 채워져 있지만, 레벨3에서 왼쪽부터 채워져 있지 않아서 완전 이진 트리가 아님.

---

3️⃣이진트리 구현

• 이진트리는 연결리스트를 이용하는게 더 직관적이라 연결리스트 사용할 것임
• 이진 트리의 ADT 즉,추상 자료형을 정의 해보겠다.

이진트리의 추상자료형 구현하기

노드 생성

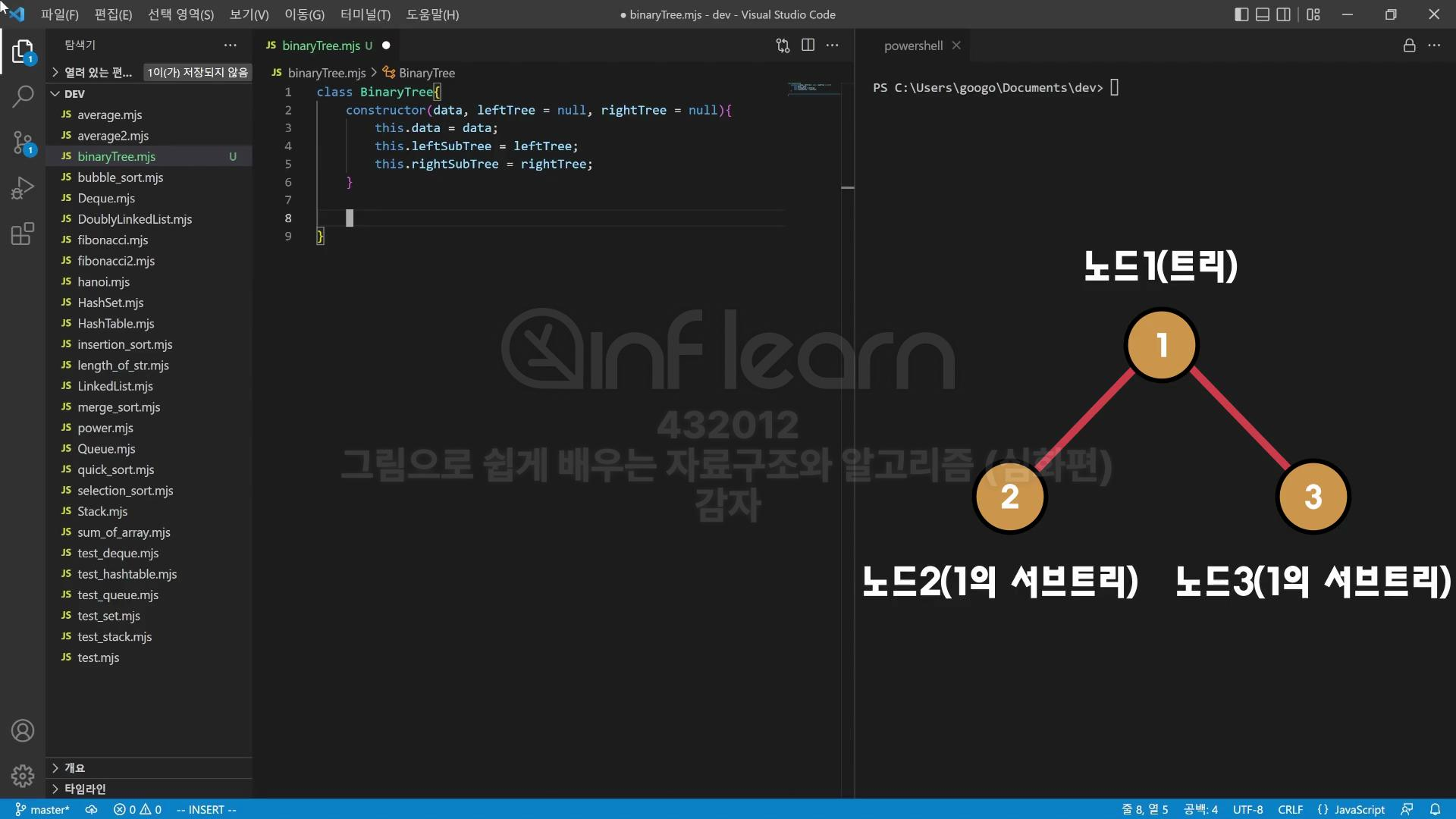
class BinaryTree {
  constructor(data, leftTree = null, rightTree = null) {
    (this.data = data),
      (this.leftSubTree = leftTree),
      (this.rightSubTree = rightTree);
  }
}
 

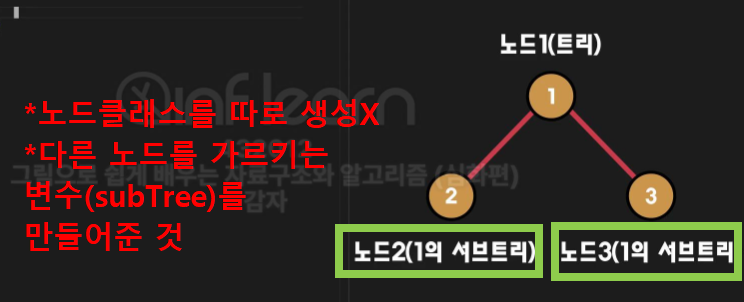
노드를 1개만 만든 이유

• 이진트리는 노드이면서 트리이기 때문!
• 노드2는 노드1의 서브트리
• 노드3은 노드1의 서브트리
  

이진트리 메서드 구현

  getData() {
    return this.data;
  }

  setData(data) {
    this.data = data;
  }

  getLeftSubTree() {
    return this.leftSubTree;
  }

  getRightSubTree() {
    return this.rightSubTree;
  }

  setLeftSubTree(tree) {
    this.leftSubTree = tree;
  }

  setRightTree(tree) {
    this.rightSubTree = tree;
  }

---

트리 만들기

• 이제 트리를 만들 test_binaryTree.mjs파일을 만들었다.
• 이중에서 가장 먼저 해야할 것은 7개의 노드이자 트리를 만드는 것 이다.
  

//1. 7개의 노드(트리)만들기
let tree1 = BinaryTree(1);
let tree2 = BinaryTree(2);
let tree3 = BinaryTree(3);
let tree4 = BinaryTree(4);
let tree5 = BinaryTree(5);
let tree6 = BinaryTree(6);
let tree7 = BinaryTree(7);

//2. 연결하기
tree1.setLeftSubTree(tree2);
tree1.setRightSubTree(tree3);
tree2.setLeftSubTree(tree4);
tree2.setRightSubTree(tree5);
tree3.setLeftSubTree(tree6);
tree3.setRightSubTree(tree7);

• 노드를 만들고, 각자 노드를 연결하였을때 직접 콘솔에 호출해보자

//3. 트리 출력하기
console.log("루트노드의 오른쪽 자식 : " + tree1.getRightSubTree().getData());

console.log(
  "루트도의 오른쪽 자식의, 왼쪽 노드 : " +
    tree1.getRightSubTree().getLeftSubTree().getData()
);

• 그러면 터미널창에 정상적으로 노드에 입력한 값이 잘 호출되었다.

만약, 트리 '전체'를 출력하려면 하나씩 다 '수동'으로 입력하기?
너무 힘들고 귀찮다.
그러니 트리 '전체'를 출력하는 기능 을 구현하기 !

---

순회로 전체 출력

그림으로 먼저 파악

• 이렇듯, 높이가 2 인 트리는 전위순회+중위순회+후위순회로 전부 출력 할 수 있다.

만약 높이가 7인 트리를 중위 순회 하자면 ?
이미지 처럼 모든 노드가 재귀적으로 출력 되어야 함.

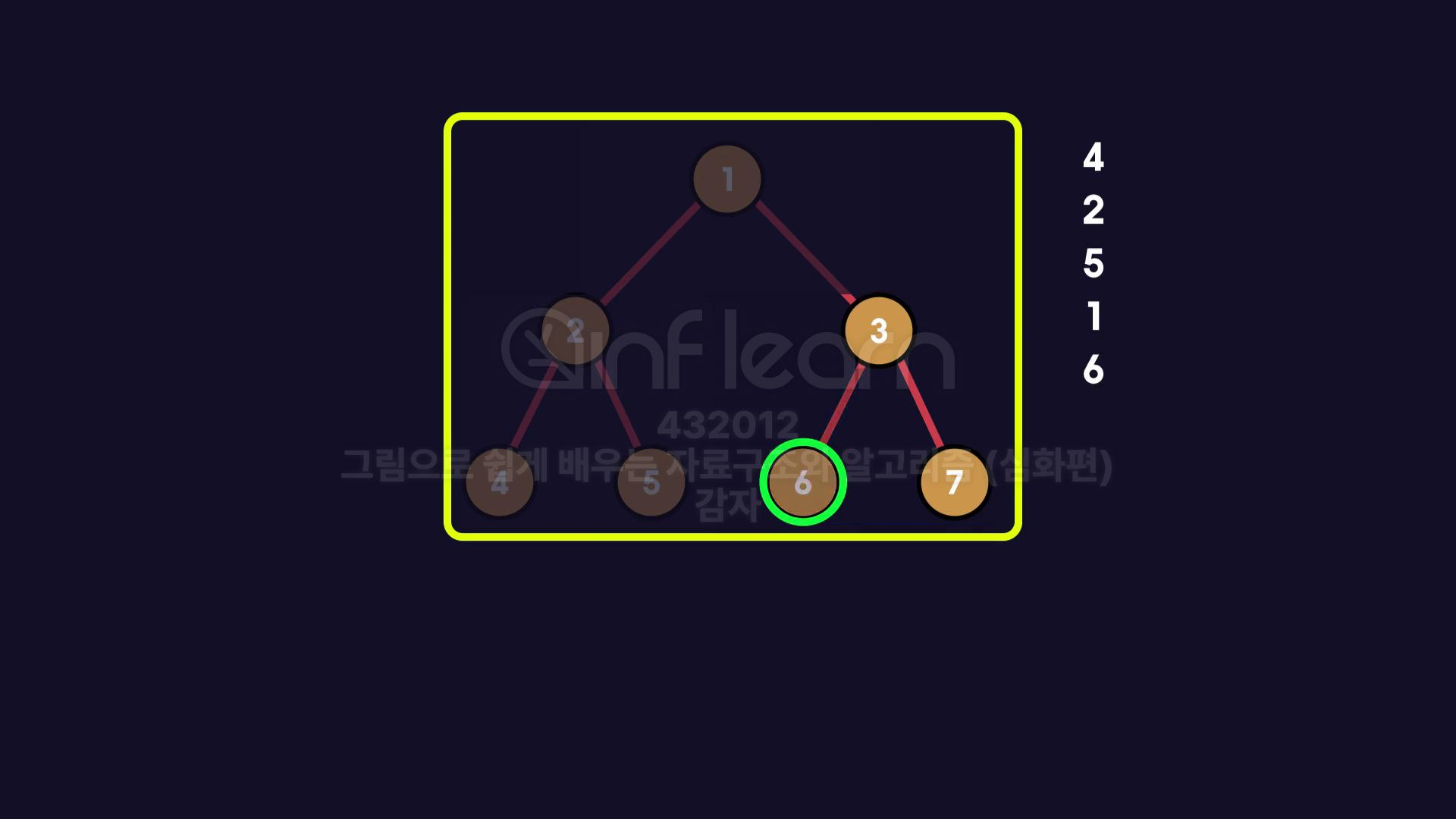
전위순회 구현

 // 전위순회
  preOrderTraversal(tree) {
    //기저조건
    if (tree == null) return;
    //1. 노드호출
    console.log(tree.data);
    //2. 왼쪽 호출
    this.preOrderTraversal(tree.getLeftSubTree());
    //3. 오른쪽 호출
    this.preOrderTraversal(tree.getRightSubTree());
  }

• 전위순회, 중위순회, 후위순회도 위와 같은 방식으로 호출해 주면 된다.
• 재귀를 이용하여 모든 노드를 순회하였다.

전체 노드 호출하기

//* 전위순회 호출
console.log("전위 순회 호출");
tree1.preOrderTraversal(tree1);

//* 중위순회 호출
console.log("중위 순회 호출 ");
tree1.inorderTraversal(tree1);

//* 후후위순회 호출
console.log("후위 순회 호출 ");
tree1.postorderTraversal(tree1);

• 결과값

---

마무리

• 이진트리의 개념과, 포화이진트리 완전이진트리에 대해 알게되었다.

  포화 이진 트리: 모든 노드가 0개 또는 2개의 자식을 가지고, 모든 층이 꽉 채워져 있는 트리.
  완전 이진 트리: 마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있고, 마지막 레벨의 노드가 왼쪽부터 순서대로 채워진 트리.

• 또한, 이진트리 구현하기 위해 노드를 생성하고 트리들을 채우고
• 각 노드를 재귀로 순회하며 전체 트리를 호출하는 법을 배우게 되었다.

회고

• 재귀로 순회하는 로직을 알겠으나,
• 생성자를 통해 노드를 생성하고, 서브트리를 만들어서 기능 설정하는 부분이 익숙하지 않아서 어려웠다.
• 추후, 이번 강의에 대한 <기본편> 학습이 더욱 필요하다는 것을 깨달았다.