Leetcode 62. Unique Paths

m = 3, n = 7 일 때, 완전탐색으로 푸는법을 접근해보면,
8개 중 오른쪽(→) 6개를 선택해서 배치하는 방법
= 8개 중 아래(↓) 2개를 선택해서 배치하는 방법
8C6 = 8x7 / 2x1 = 28

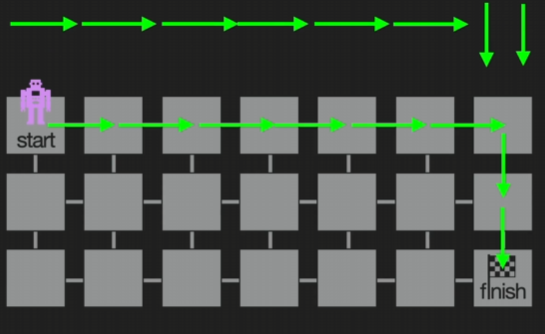
왼쪽에서 오는 경우의 수와 오른쪽에서 오는 경우의 수를 더한 값이현재 좌표의 값이 된다.

-1 또는 0으로 초기화해주고 dp[0][0] 을 1로 설정

const dp = [
  [1, 0, 0, 0, 0, 0, 0],
  [0, 0, 0, 0, 0, 0, 0],
  [0, 0, 0, 0, 0, 0, 0]
];

이런식으로 왼쪽에서 오는 경우의 수+오른쪽에서 오는 경우의 수로 현재 dp 값을 구한다

dp[1][1] = dp[0][1] + dp[1][0] = 0 + 1 = 1;

dp[1][2] = dp[0][2] + dp[1][1] = 0 + 1 = 1;

모든 갱신이 끝난 후 값

const dp = [
  [1, 1, 1, 1, 1, 1, 1],
  [1, 2, 3, 4, 5, 6, 7],
  [1, 3, 6, 10, 15, 21, 28]
];

Top-down (완전탐색 + Memoization)

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function(m, n) {
  const memo = Array(m).fill().map(() => Array(n).fill(-1));

  const dp = (r, c) => {
    // 기저 조건, 가로세로 0이면 1로 채움
    if (r === 0 && c === 0) {
      memo[r][c] = 1;
      return memo[r][c];
    }

    // 이미 계산된 경우
    if (memo[r][c] !== -1) {
      return memo[r][c];
    }

    // 왼쪽과 위쪽에서 오는 경우의 수를 더함
    let paths = 0;
    if (r - 1 >= 0) {
      paths += dp(r - 1, c);
    }
    if (c - 1 >= 0) {
      paths += dp(r, c - 1);
    }

    // 계산된 값을 memo에 저장하고 반환
    memo[r][c] = paths;
    return memo[r][c];
  };

  return dp(m - 1, n - 1);
};

Bottom-up

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function(m, n) {
  // memo 배열 초기화
  const dp = Array(m).fill().map(() => Array(n).fill(0));

  // 시작점에서의 경우의 수는 1
  dp[0][0] = 1;

  // 나머지 칸의 경우의 수 계산
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      // 왼쪽과 위쪽에서 오는 경우의 수를 더함
      if (i > 0) {
        dp[i][j] += dp[i - 1][j];
      }
      if (j > 0) {
        dp[i][j] += dp[i][j - 1];
      }
    }
  }

  // 마지막 칸의 경우의 수가 최종 답
  return dp[m - 1][n - 1];
};