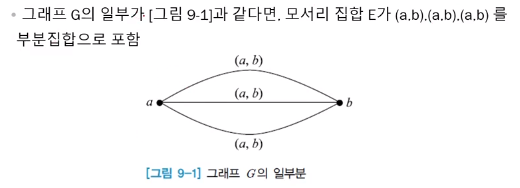
ref : http://www.kocw.net/home/search/kemView.do?kemId=1335653
그래프유형 : 다중, 방향, 가중치
차수 : 홀수, 짝수, 외차수, 내차수
그래프 종류 : 부분, 부분신장, 동형, 평면, 연결, 환전, 정규, 이분, 완전이분
그래프 표현 : 인접, 인접리스트
순환: 순환, 길이
오일러 그래프: 오일러 경로, 순환(회로), 오일러 그래프
해밀턴 그래프: 해밀턴 경로, 해밀터 순환(회로), 해밀턴 그래프
그래프의 활용: 최단경로문제, 깊이우선탐색, 너비우선탐색
1. 그래프의 개념
Graph = 그래프
순서쌍으로 표현.
n개의 점과 m개의 선으로 구성.
Adjacent = 인접, Incident = 근접
Loop = 루프
예제

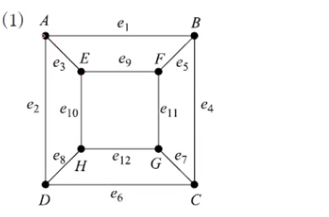
1.2 그래프의 형태
Multi-graph = 다중그래프
Directed Graph = 방향그래프
표현은 < > 사용!!
directed graph 예시
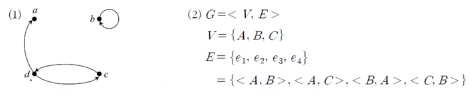
Weighted Graph = 가중치 그래프

W[node1,node2] 로 표현
가중치 예시
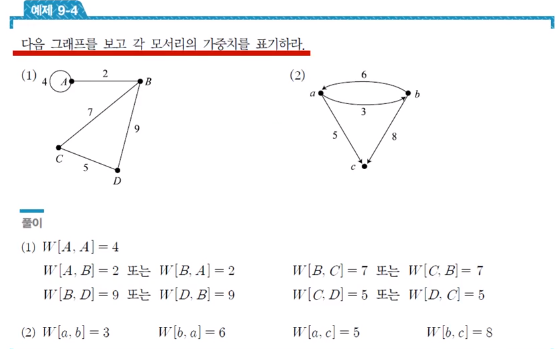
1.3 그래프의 차수
Degree = 차수
node에 연결된 edge 수
d(node)로 표현.
방향그래프에서 차수 : out-degree, in-degree
방향그래프의 loop의 경우 내, 외차수 모두 카운트함.
차수 예시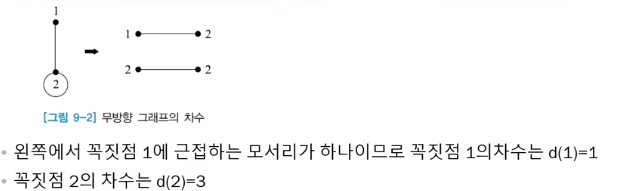
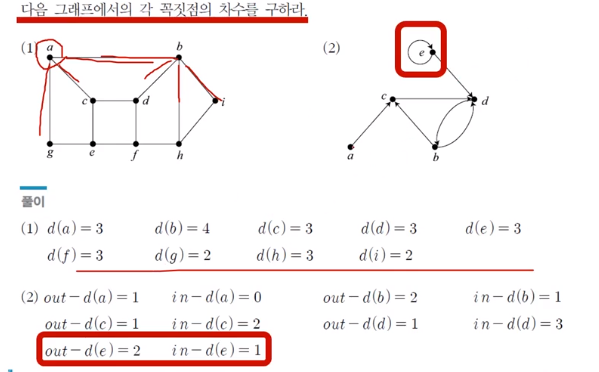
차수 정리/성질과 증명
 number of Odd degree - node is even number
number of Odd degree - node is even number 
관련 예제

2. 그래프의 종류
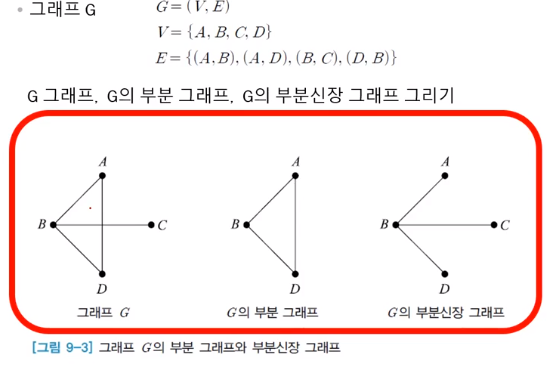
* Subgraph = 부분 그래프
* spanning graph = 부분신장 그래프
부분그래프, 부분신장 그래프 예시
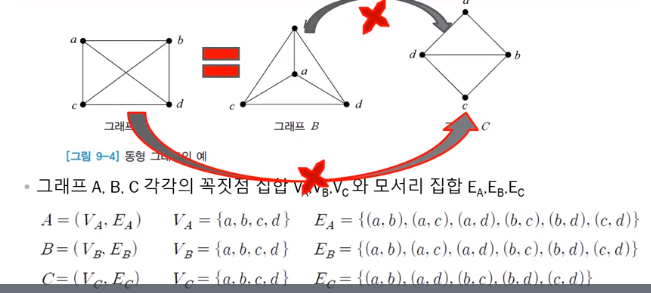
* Isomorphic Graph = 동형 그래프
꼭지점수, 연결선 수 동일!!
one to one correspondence : 역함수가 존재함.
한 x 당 한 y 값있음. 노는 y값 없음
동형그래프 예시
* Planar Graph = 평면 그래프
점에 모이는 건 괜찮음!
평면그래프 예시
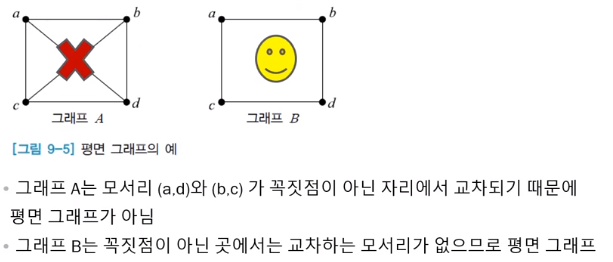
- 만약 1번예시에 가운데 node가 있었다면 평면그래프 성립
평면그래프의 영역
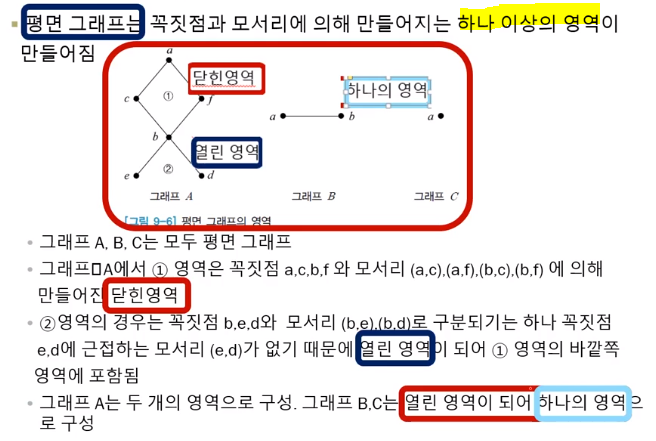
평면그래프의 오일러 공식의 성립 Euler's formula

num of node - num of edge + 영역 = 2
증명

* Connected Graph = 연결그래프
- 그래프를 구성하는 모든 꼭지점 사이에 경로가 존재하는 그래프!
Walk = 길
Path = 경로
연결그래프 예시 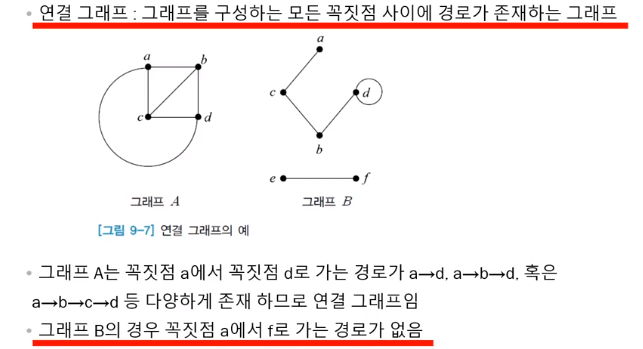
* Complete graph = 완전 그래프

- 모든 node의 degree가 n-1개
- 모든 노드가 서로 이어져있음!
완전그래프 예시
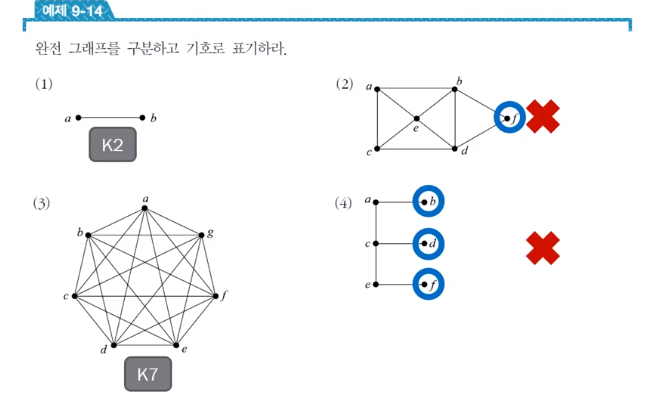
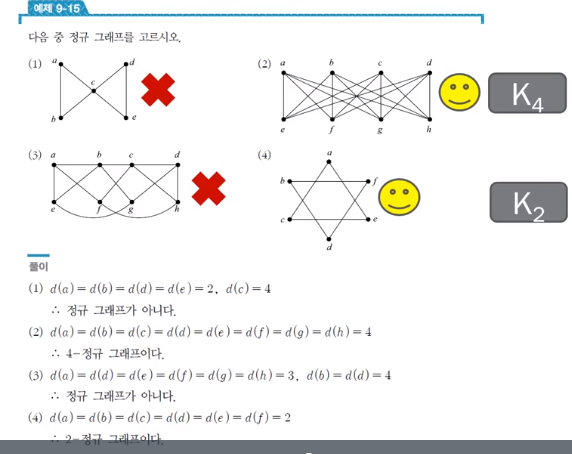
* Regular graph = 정규그래프
- all node have same degree
정규그래프 예시
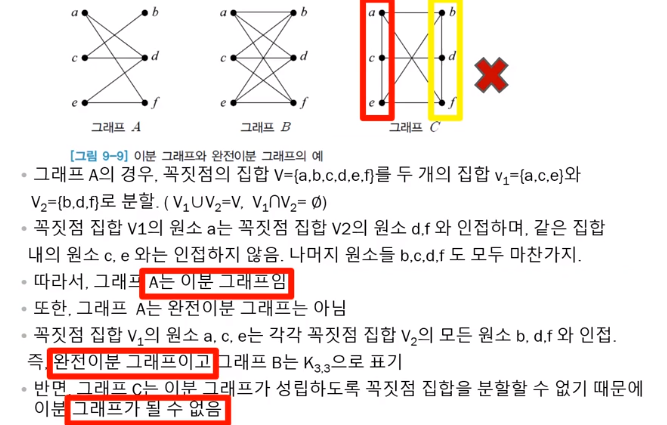
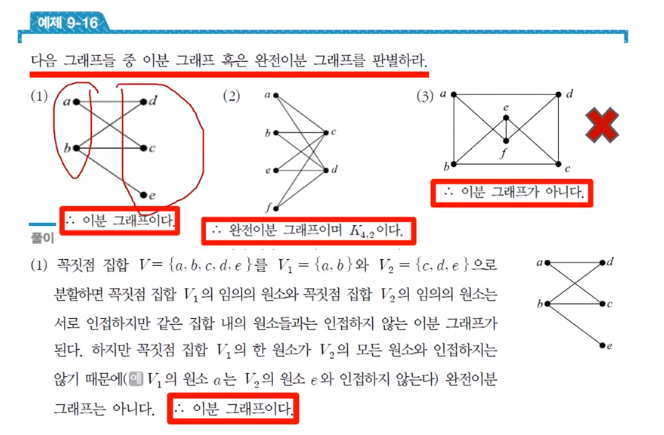
* Bipartite Graph = 이분 그래프
- 그래프 내에 꼭지점 집합을 분할하고 분할로 만들어진 서로다른 노드 집합류 사이에 edge이 존재하면 이분그래프
- 나눠진 분할집합 내의 노드끼리는 이어지면 안됌
* Complete Bipartite graph = 완전이분그래프
이분그래프 예시
3. 그래프의 표현
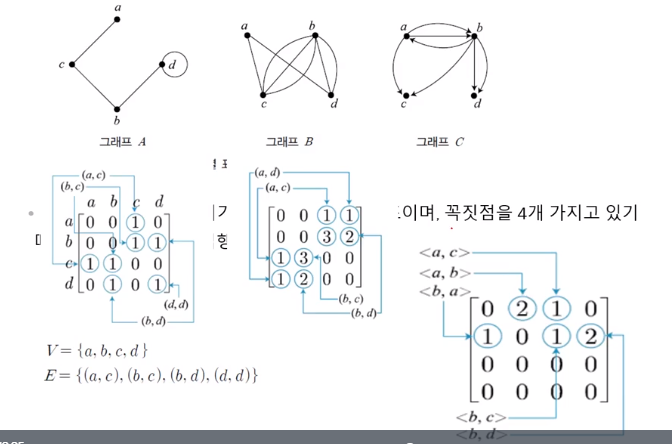
* Adjacency Matrix = 인접행렬
인접행렬 예시
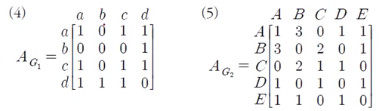
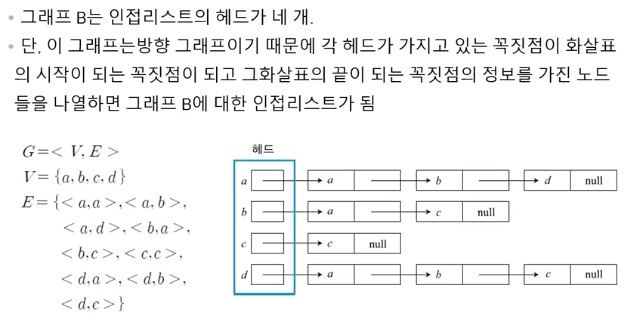
Adjacency List = 인접리스트
- 연결된 node를 표현.
인접리스트 예시

4. 오일러와 해밀턴
- 오일러 그래프는 edge 기준.
- 해밀턴은 node 기준으로 정의
Cycle, Circuit = 순환, 회로
length
경로에 관한 개념
- walk 길 : A에서 B로 도착하기 위한 정점과 모서리의 나열
- Path 경로 : 같은 모서리를 두 번 이상 포함하지 않는 길
- Length 길이 : 경로를 구성하는 모서리 개수
경로와 길이 예시 문제

* Eulerian Graph 오일러 그래프
Eulerian Path & Cycle

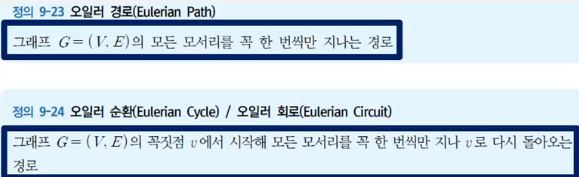
- 모든 모서리를 딱 한번만!!
- 오일러 그래프가 되러면 순환이 성립해야해! -> 한붓그리기가 가능하냐.
오일러 경로, 순환, 그래프 예시
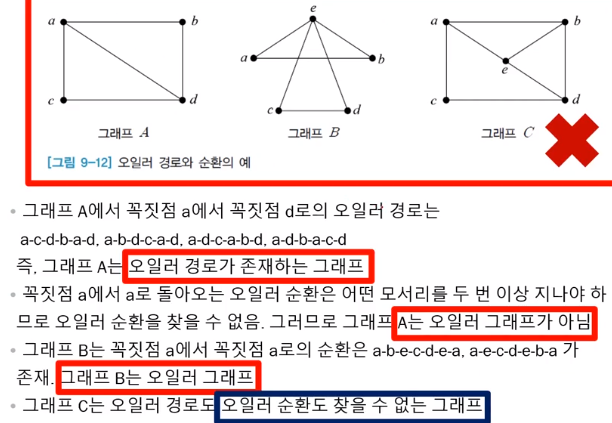
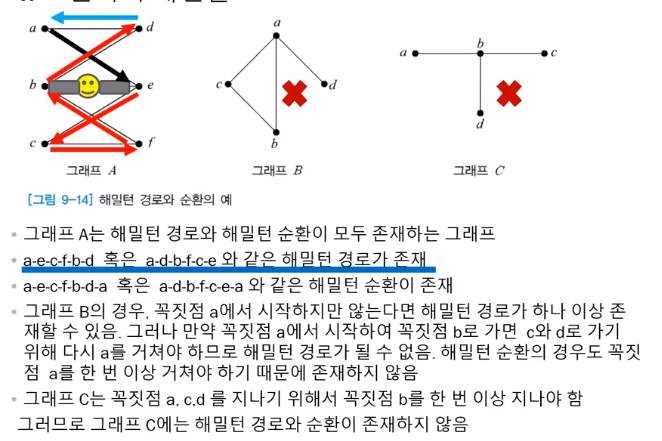
- A의 경우 오일러 경로가 존재하지만 오일러 그래프는 아님.
- B는 오일러 순환을 가지니까 그래프
오일러 그래프의 특징
오일러 그래프 쉽게 판별하기
- 모든 node의 degree가 짝수이거나(홀수 node 0개) degree가 홀수인 node가 2개면 오일러그래프!



해밀턴 정의
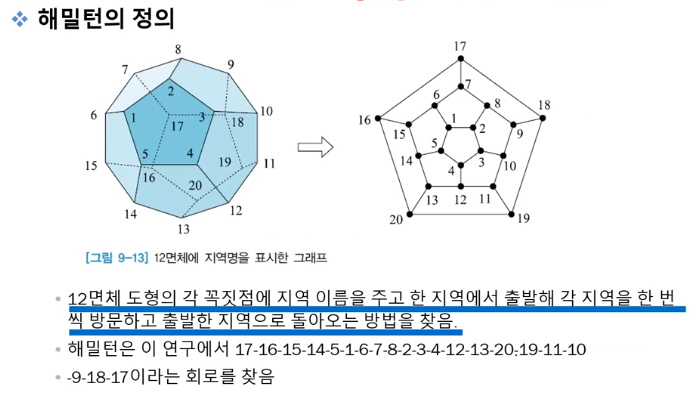
* Hemilton Graph 해밀턴 그래프
Hemilton Path & Cycle

- 해밀턴 경로와 순환은 edge를 몇 번 지나던 혹은 안 지나던 상관없고 오직 node 만 한번씩 !!!
해밀턴 그래프 성질 증명

해밀턴 경로, 순환, 그래프 예시
5. 그래프의 활용
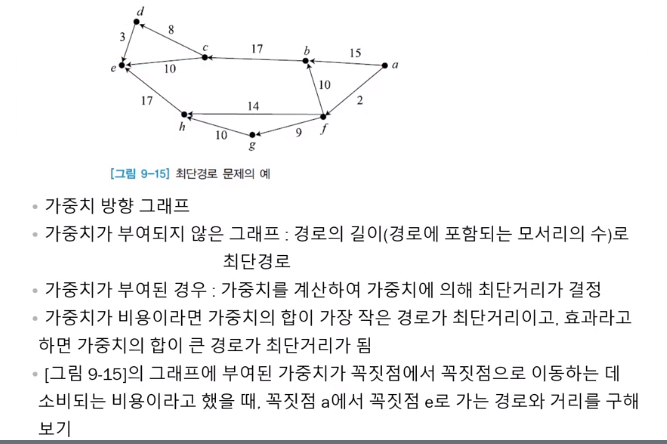
Shortest Path Problme 최단 경로 문제
- edge는 1개이상.
최단경로 문제 예시
- 가중치의 유무에 따라 풀이에 차이가 있음.

- 다익스트라 알고리즘 기호와 가정


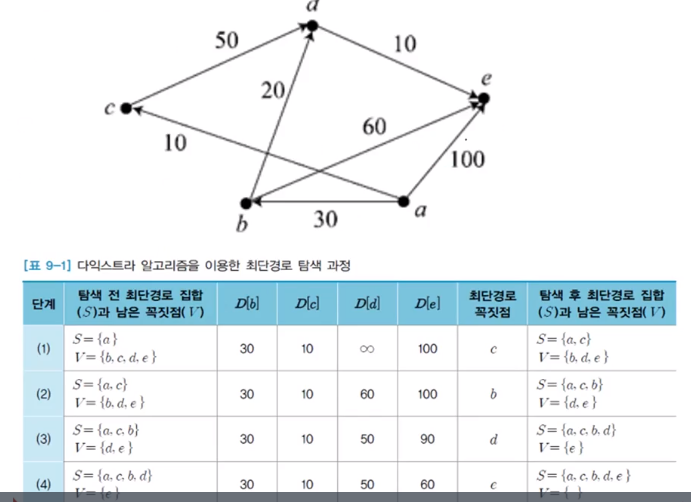
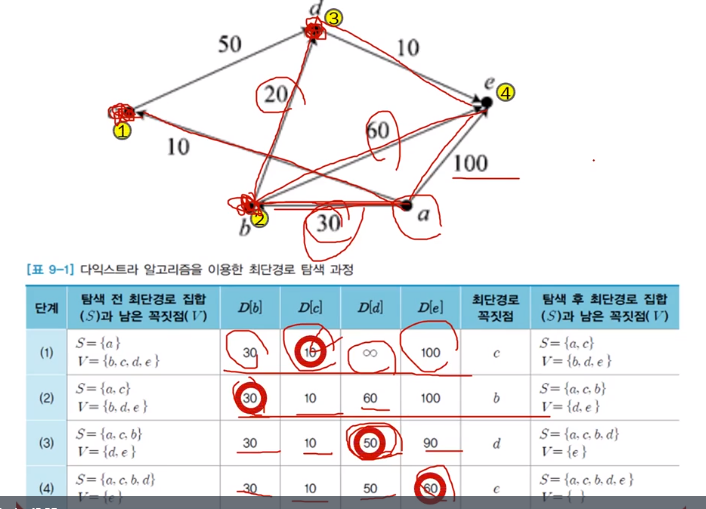
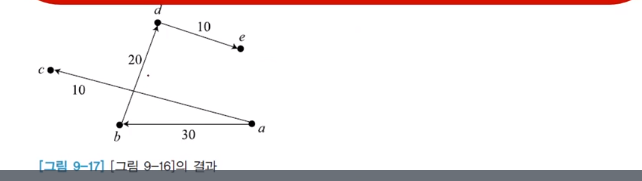
다익스트라 알고리즘
예제
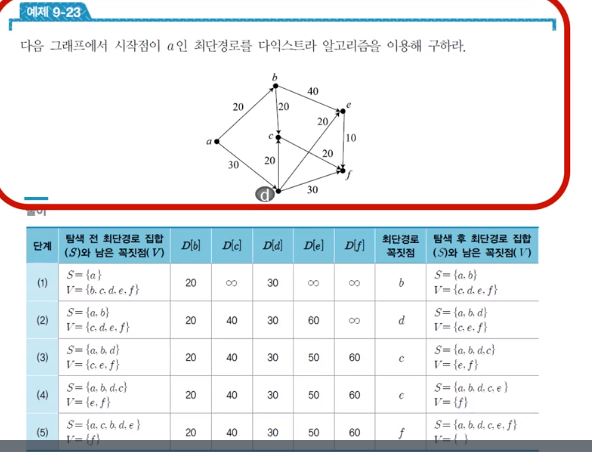
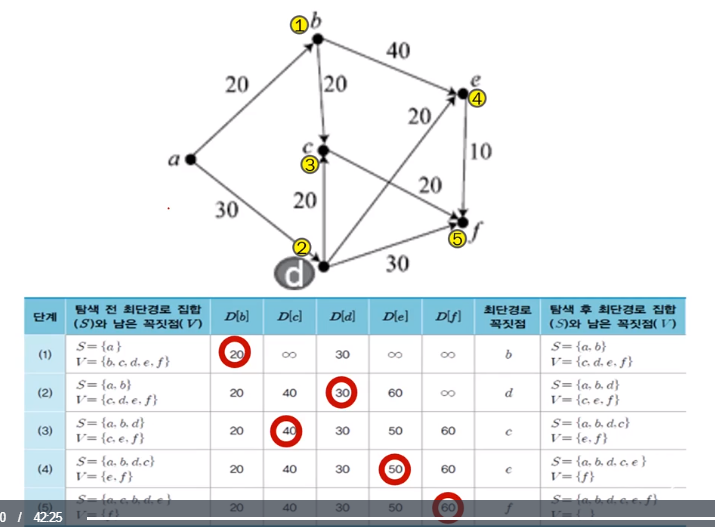
깊이 우선 탐색
- 예를들면 알파벳순서를 고려함.
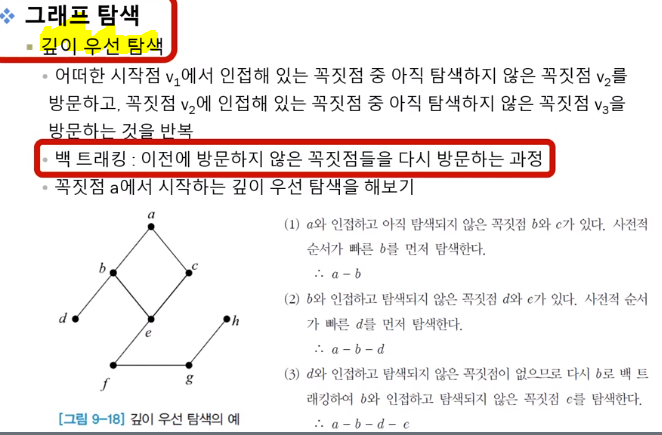
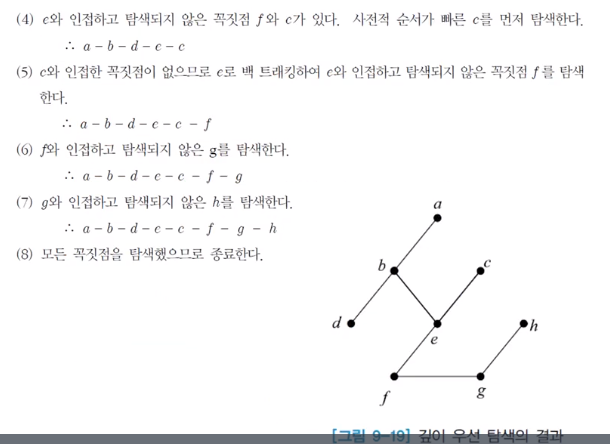
너비 우선 탐색
- 트리모양에서 위에서 아래로 왼쪽 오른쪽으로 훑으며 쭉 내려옴.