HiPPO: Recurrent Memory with Optimal Polynomial Projections
1. 시작하며
저번주에는 머리를 싹둑 잘랐습니다. 조교로 참여했던 2023 fastmri challenge가 무사히 끝났습니다. 작년엔 참가자로 참여했었고 올해는 조교로 대회를 운영했습니다. 급여도 만족스러웠고(^.^) 대회를 관리하면서 다각도에서 대회를 체험할 수 있어 뜻 깊었습니다.


그와 별개로 기술자(교수) 추천 시스템 프로토타입을 개발하는 일도 쓱싹쓱삭 하고 있습니다. 센터장님의 carbon copy 해주신 메일을 보니 어깨가 더 무거워지네요. 프로토타입이라서 간단하게 2-3주 작업하면 끝날 줄 알았는데요. 벌써 3달째입니다.

네, 간단한 근황이었고요. 매주 진행하고 있는 연구실 세미나 시간에는 transformer 유의 논문들을 리뷰하고 있습니다. 저번주에 저는 hungry hungry hippos (H3)라는 논문을 리뷰하는 발표를 했었습니다. language modeling에서 transformer 유의 모델의 성능을 능가했다는 점에서 의미심장했지요. 한편, 이번주에는 H3의 근간이되는 HiPPO (high order polynomial projection)에 관해서 리뷰해보려고 합니다. HiPPO는 어떤 시간 간격이 되었든 과거의 정보를 십분 반영해서 정보의 손실이 RNN, LSTM에 비해 현저히 적다는 큰 장점이 있습니다. 논문 제목은 아래와 같습니다. 살펴보시지요.
HiPPO: Recurrent Memory with Optimal Polynomial Projections
준비한 슬라이드 주소입니다: https://docs.google.com/presentation/d/12k8IAwJQjHv6sB31x-BnzNtRr4lBtJJAUaiqa5yH0E0/edit?usp=sharing
2. paper review
Motivations
HiPPO는 시계열 데이터를 위한 모델입니다. 저장 공간이 유한한 이슈로인해 cumulative history를 전부 반영하는 representation을 학습하는데 큰 한계가 있습니다. 이때의 representation은 데이터가 계속해서 들어오는 online 알고리즘에서 실시간으로 update 되어야 합니다. 시계열 데이터를 다루기 위한 RNN, Fourier Recurrent Unit(FRU), Legendre Memory Unit(LMU) 등은 모두 sequence length를 prior로 요구하고 있습니다. 즉, hidden state, context variable 등에 cumulative history가 전부 반영되지 않는다는 원천적인 문제점을 지니고 있습니다.
이 문제점에서 영감을 얻어 HiPPO의 아이디어를 발전시켰습니다. 특히, 추후 등장할 HiPPO-LegS는 seqeunce length 등과 같은 prior가 전혀 필요하지 않고 모든 timescale을 정보를 반영할 수 있습니다. 그뿐만아니라, HiPPO-LegS는 asymptotically more efficient updates, bounds on gradient flow 와 approximation error의 이론적 특성이 있습니다. (논문의 부록에 자세히 증명되어있습니다.)
HiPPO의 특이사항으로는 deep learning model과는 다르게 learnable parameter가 전혀 없다는 것 입니다. RNN, LSTM, GRU등은 Low order Polynomial Projection Operator으로 볼 수 있다고 합니다.
What is HiPPO trying to do?
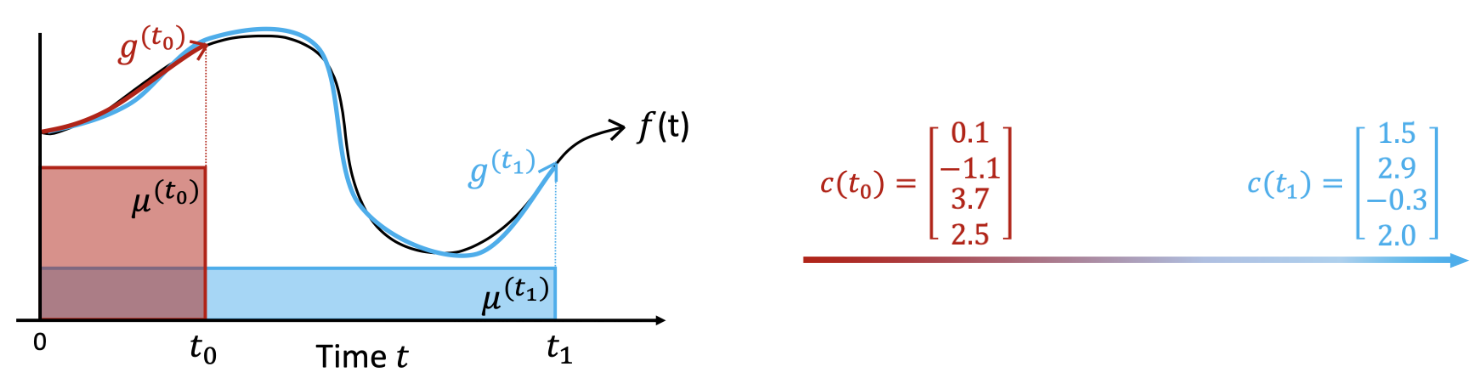
HiPPO는 한마디로 online function approximation 입니다. 위의 그림과 같이 f(t)라는 ground truth input이 주어졌을때, 정보의 손실을 최소화하는 방향으로 g(t)를 얻어낼 수 있습니다. 이때, g(t)는 orthogonal polynomials(OP)를 활용해서 구할 수 있습니다. 각 orthogonal polynomial basis에 f(t)를 사영시켜 reconstruction을 하면 그것이 바로 g(t)가 되는 것 입니다.
위의 예시에서는 orthogonal polynomial basis(OP basis)가 4개입니다. 각각의 coefficient (c(t))는 해당 시점에서 OP basis에 사영(projection)된 값을 나타냅니다.
t가 점점 증가해도 (t0, t1에서의 각 g(t0), g(t1)을 유심히 살펴보면 알 수 있듯) OP basis에 f(t)를 projection하여 [0, t]의 f(t) 정보를 유지할 수 있는 점이 바로 HiPPO의 핵심입니다.
그림에서 등장하는 는 바로 다음의 Orthogonal Polynomials에 대해서 자세히 이야기 할 때 더 확실히 알 수 있습니다.
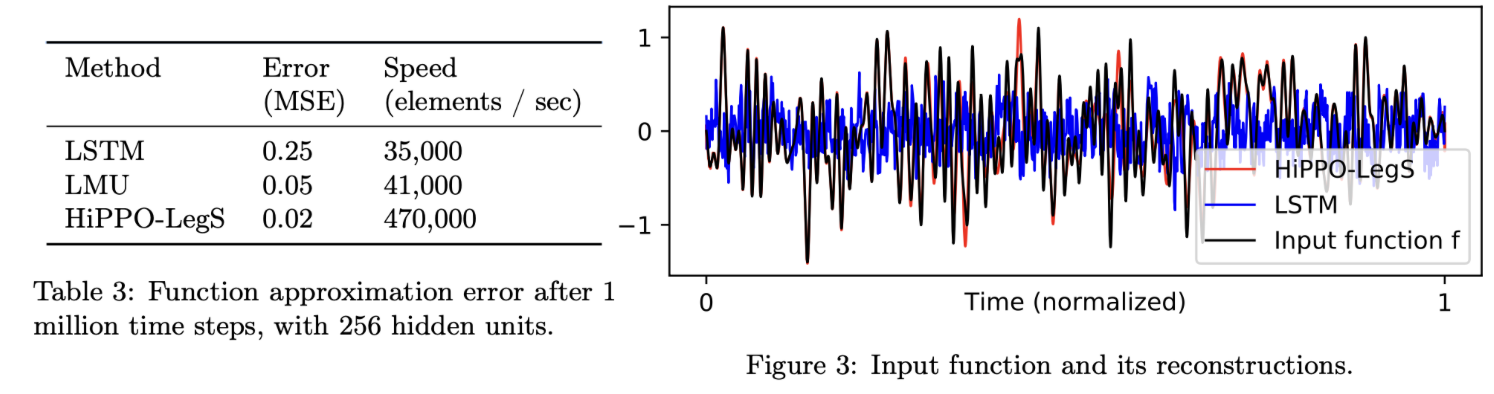
위의 그림은 LSTM, LMU(Legendre Memory Unit), HiPPO-LegS 의 reconstruction을 비교한 그림입니다. 길이의 White noise를 input으로 합니다. Memory는 256 units을 넘기지 못한다는 제한 조건이 있습니다. 오른쪽의 시그널을 맨눈으로 봐도 HiPPO-Legs가 훨씬 더 정교하게 input을reconstruction 했음을 확인 할 수 있습니다. 물론, 다른 모델들 보다도 10배를 초과하는 속도를 지니고 있기도하지요.
Orthogonal Polynomials (OP)
Orthogonal Polynomials은 ML 분야에서 다각도로 활용되고 있습니다. 그 예시는 아래와 같습니다.
1) automatic algorithm design
2) model compression
3) replacing hand-crafted preprocessing in speech recognition
이젠 HiPPO도 빼놓을수 없겠죠?
Orthogonal Polynomials는 다항식으로 함수식을 근사하기 위해 발전된 개념입니다. 다양한 Orthogonal Polynomials가 존재하는데요. 그 예시로는 아래와 같습니다. 그외에도 Polynomials는 아니지만 Fourier basis 역시 비슷한 개념으로 생각할 수 있습니다.
1) Legendre
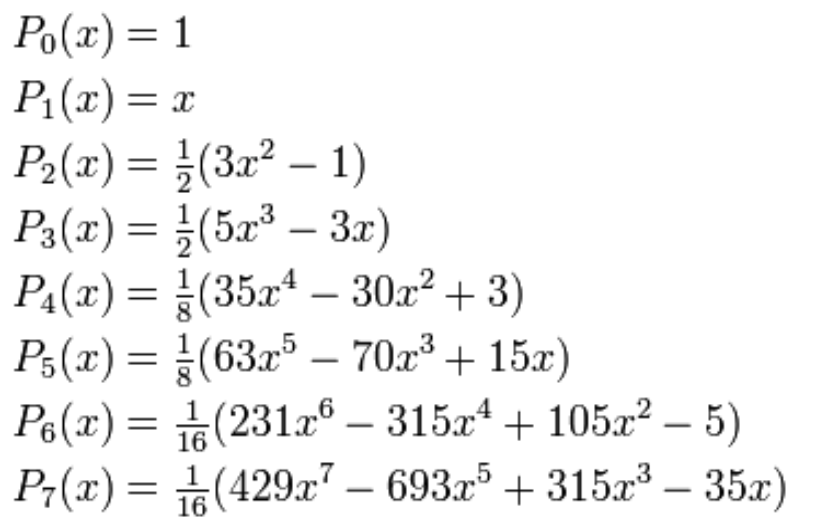
2) Laguerre (화질 이해바랍니다.)
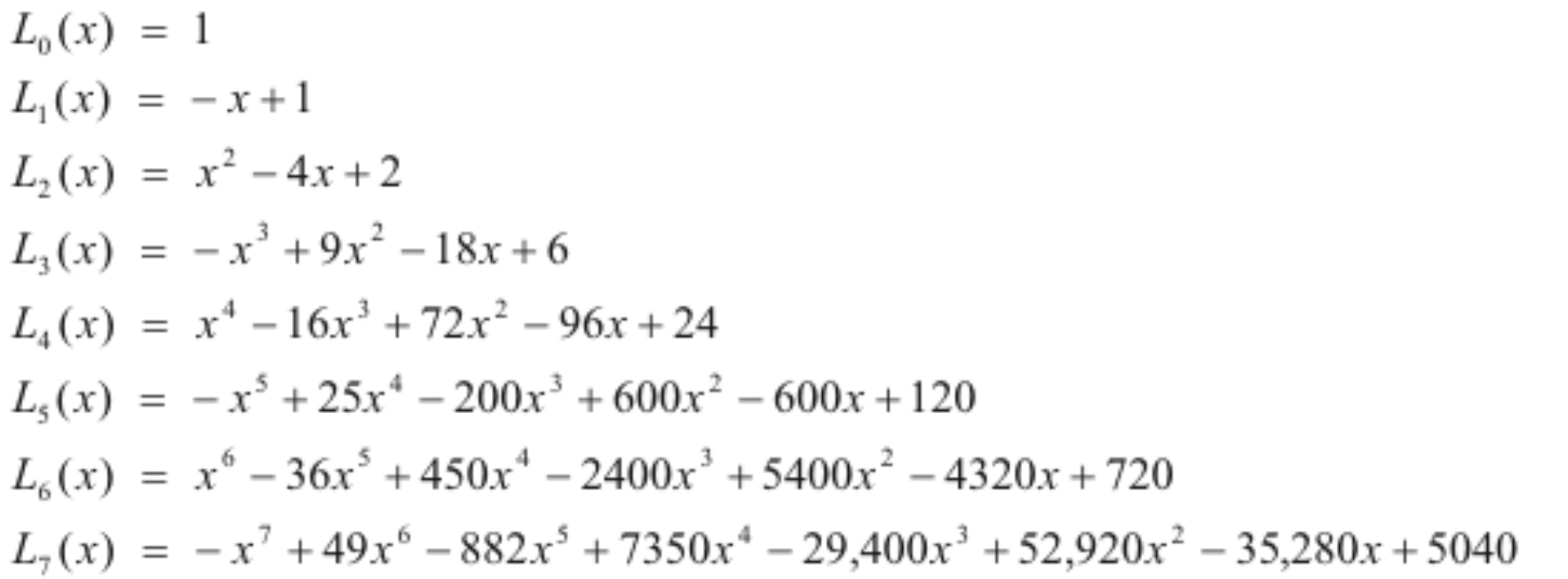
3) generalized Laguerre
4) Hermite
5) Chebyshev (화질 이해바랍니다.)
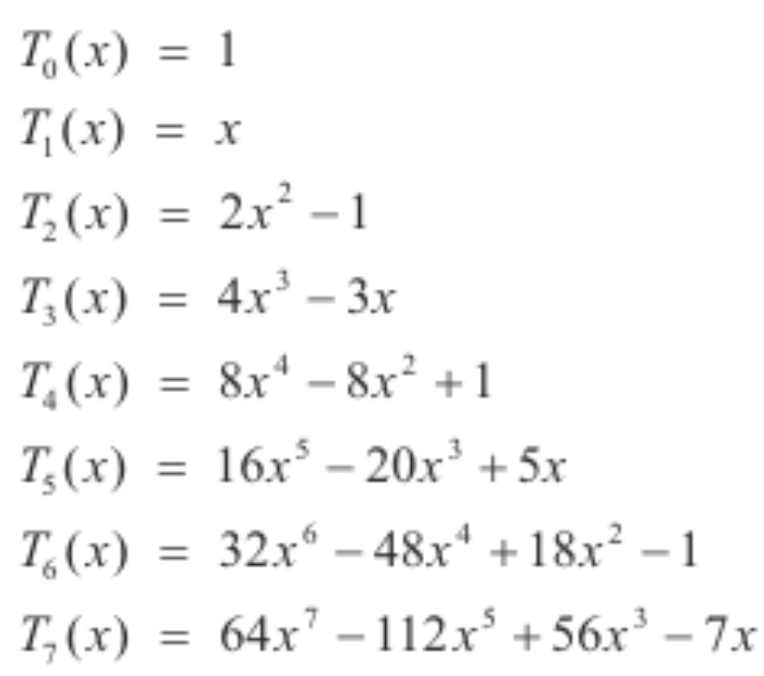
OP는 measure과 basis를 활용해서 정의할 수 있습니다. measure과 basis에 따라서 무수한 OP를 생각해볼 수 있습니다.
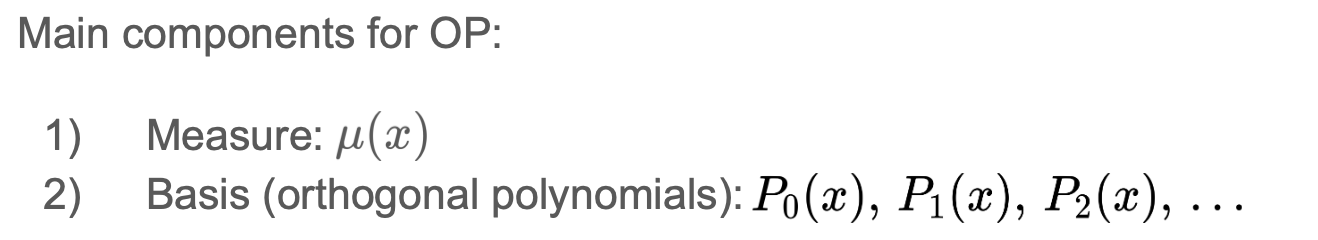
이때 위에서 정의한 measure과 basis는 아래의 특성을 지니고 있습니다.

초기 basis와 Gram-schmidt 직교화 활용하면 2)번 성질을 만족하는 basis를 찾을 수 있습니다. 3)번 성질을 활용해 함수 f를 N개의 basis(N-1 차원의 다항식)으로 복원(reconstruction)하여 나타낼 수 있습니다.
HiPPO formulation
HiPPO 연산을 알기 위해서는 아래의 정의들을 짚고 넘어가야 됩니다.
가장 먼저 measure 에 대해서 f와 g의 내적은 아래와 같이 정의할 수 있습니다. 우측의 연산은 measure 에 대한 f의 L2 norm임을 확인할 수 있습니다.
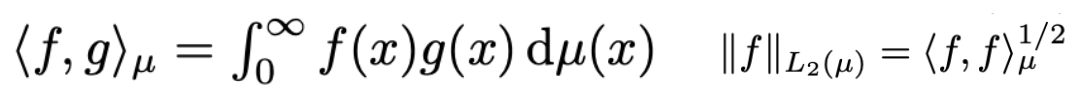
HiPPO 연산을 위해서 단 두가지의 연산이 필요한데요. 그것이 바로 와 입니다.
는 t까지의 f를 N-dimensional OP basis set이 span하는 subspace의 원소로 대응시킵니다. 이때의 원소를 로 표현하고 있습니다. 는 t까지의 f와의 error(두 함수의 차이의 measure 에 대한 L2 norm)를 최소화합니다.
는 각 OP basis에 대응되는 coefficients를 한군데 모아놓은 N-dim vector입니다.
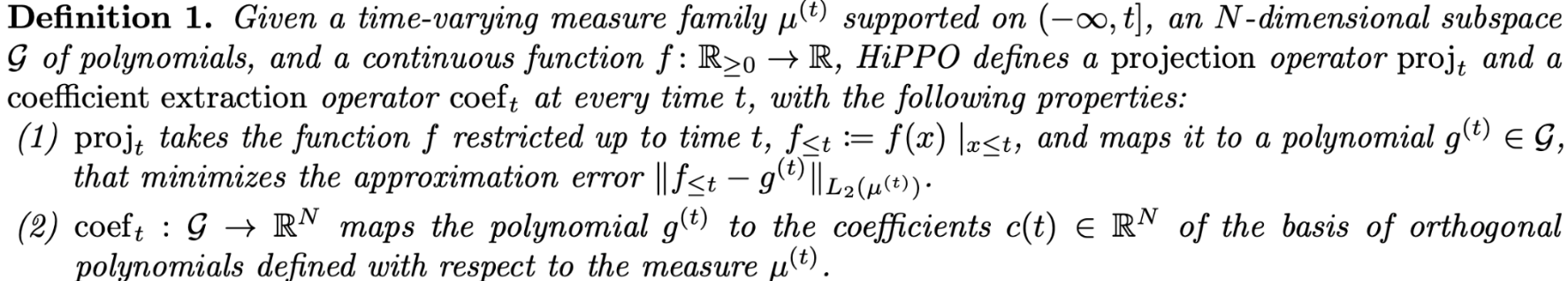
HiPPO는 앞서 정의한 와 를 순차적으로 합성한 함수로 정의할 수 있습니다.
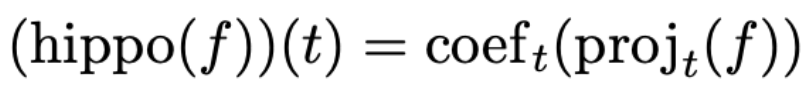
전체적인 flow는 다음과 같습니다.
(1) discrete한 f를 마치 continuous한 function으로 생각합니다.
(2) (1)에서의 f를 OP basis를 활용해 사영(projection)을 진행하고 reconstruction해 g를 얻을 수 있습니다.
(3) (2)의 g에서 각 OP basis에 대응되는 coefficient만 추출해 c를 얻습니다. c(t) = (hippo(f))(t) 입니다. 한편, c(t)에 관련된 미분방정식을 유도할 수 있습니다. (후술)
(4) 이를 discrete space로 다시 환원시켜 c에 대한 정보를 계산하기 용이하게 합니다.
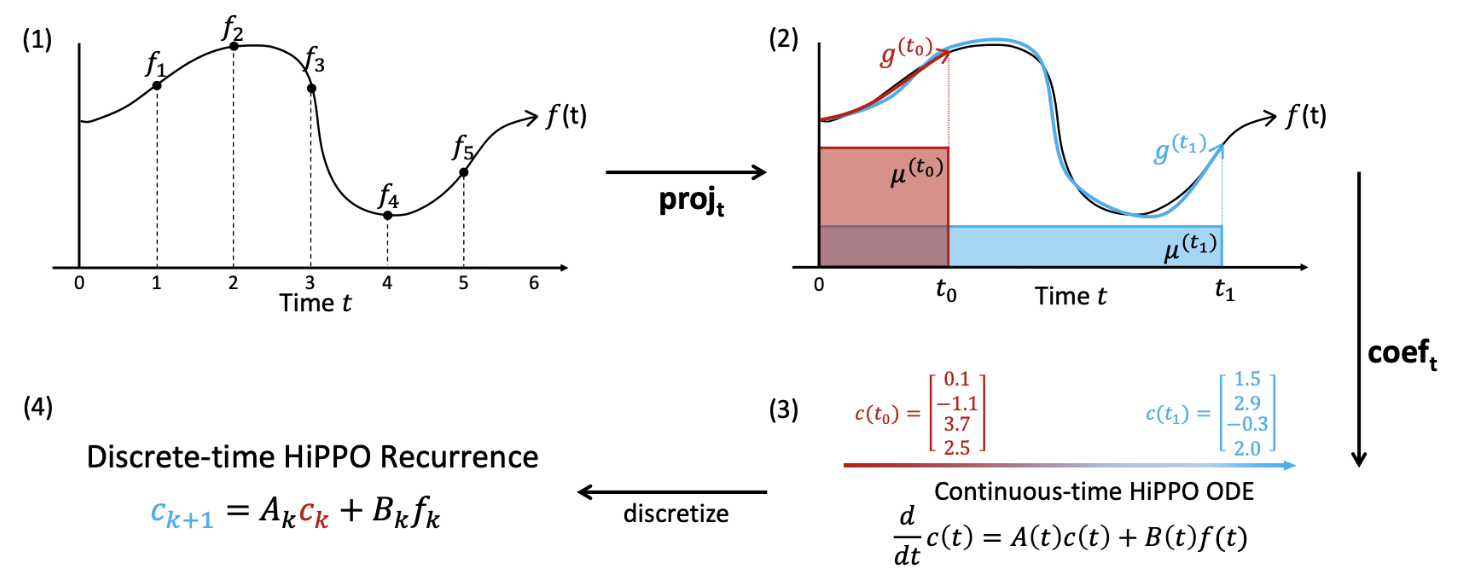
아래의 식(continuous differential eqaution)에서 첫번째 식은 HiPPO-LegT, HiPPO-LagT, 두번째 식은 HiPPO-LegS에 대한 미분방정식을 나타내고 있습니다. 논문의 부록에 자세한 유도가 등장합니다. 이 식을 자세히 살펴보면 아래의 속성을 확인할 수 있습니다.
1) N는 orthogonal polynomial basis의 개수입니다.
2) N이 작을수록 c series는 low order polynomial projection, 클수록 high order polynomial projection 입니다.
3) f(x), 0 ≤ x ≤ t 를 N-dimension의 vector로 compression을 진행해 c(t)로 표현한 것임을 확인할 수 있습니다.
4) 방정식에서 관찰할 수 있다시피 c(t)는 recurrence 속성을 지니고 있습니다.
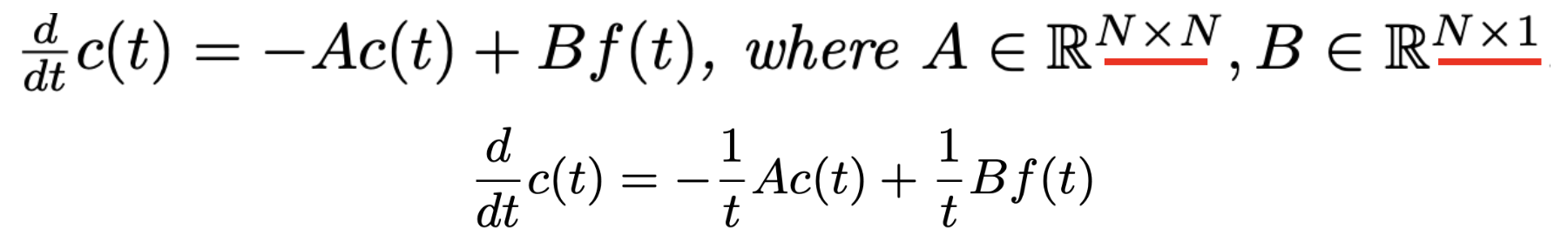
HiPPO-LegT, HiPPO-LagT and HiPPO-LegS
논문에서는 HiPPO를 measure과 OP basis에 따라 3가지를 대표적으로 제시했습니다. 그와 관련해서 내용을 표로 정리해봤습니다. Leg는 legendre, Lag는 Laguerre의 줄임말입니다. 또, T와 S는 각각 translated, scaled를 지칭하고 있습니다. translated와 scaled는 measure의 특성을 단적으로 나타냅니다. translated measure은 함수를 시간축에 대해서 평행이동시키며 활용하는 한편 scaled measure은 시간이 증가함에 따라 importance를 균등하게 재분배 해서 활용을 하고 있습니다. HiPPO-LegT만이 고정된 sequence length prior 를 필요로합니다. 나머지 두 모델은 모든 과거의 정보를 잘 반영할 수 있음을 알 수 있습니다.
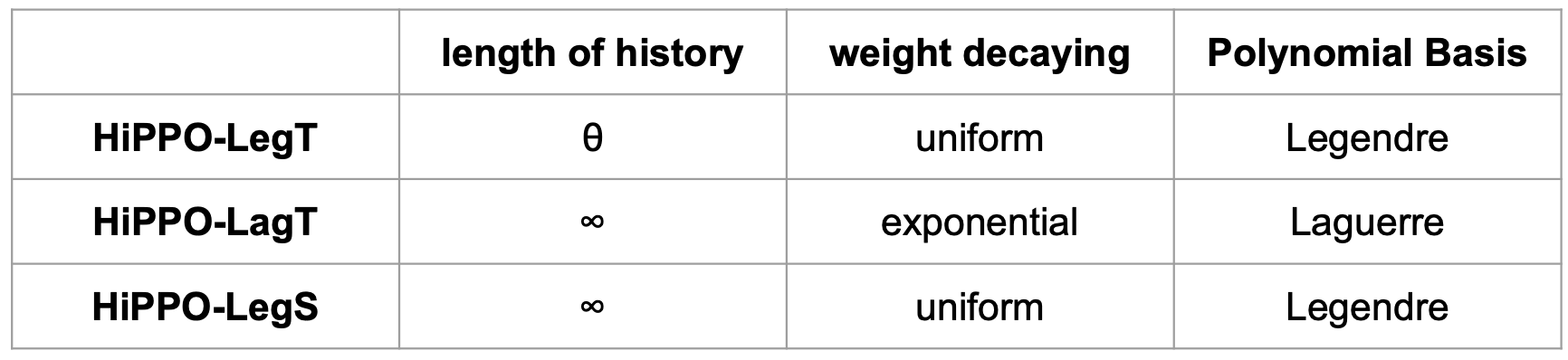
c(t)를 ( = (hippo(f))(t) ) 미분하면 continuous domain에서 미분방정식을 얻을 수 있습니다. 관련해서 논문의 부록에서 자세하게 설명하고 있는 유도과정에 대해서는 후술하도록 하겠습니다.
HiPPO-LegT, HiPPO-LagT의 미분방정식 형태
HiPPO-LegS의 미분방정식 형태
이때의 각 모델에서 A, B는 아래의 식을 만족해야만합니다. (부록에서 유도)
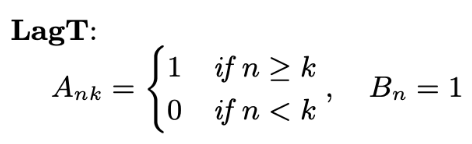
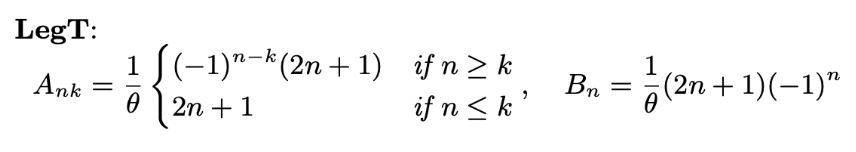
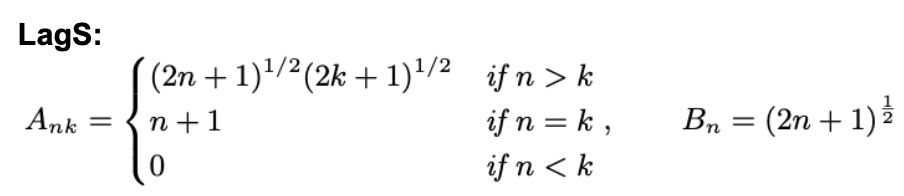
아래의 그림을 보면 더 효과적으로 이해할 수 있습니다. 각 모델에 대해서 measure을 직관적으로 표현한 것을 확인할 수 있는데요. translated measure 같은 경우는 시간축에 따라 함수를 평행이동시킨 형태입니다. 반면, scaled measure의 경우는 시간이 증가함에 따라 그 중요도(importance)가 새롭게 scaling되는 것을 확인할 수 있습니다. 더불어, 모든 measure을 모든 해당 구간에 대해서 적분하면 1이 되도록 설정했습니다.
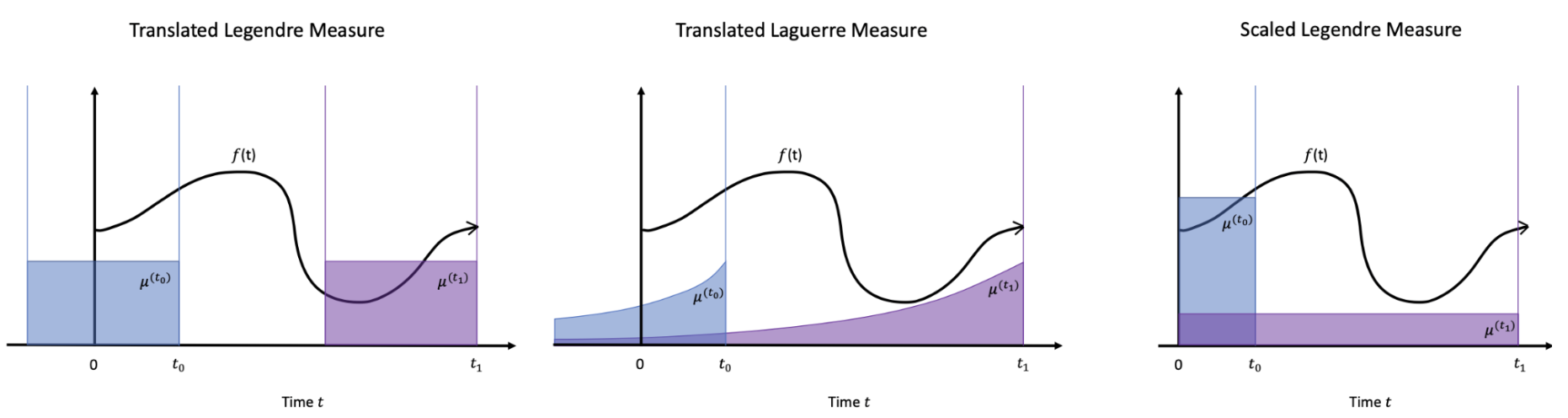
μ (measure)는 한마디로 input domain의 importance를 제어한다고 생각할 수 있습니다.
Experiments
permuted MNIST (pMNIST) data set을 활용한 대표적 실험만을 소개하겠습니다. 이 task는 sequence 전체를 보고 classification을 진행하기 때문에 시계열을 다루는 모델의 long-term dependencies 능력을 측정하는 metric을 비교할 수 있습니다. dataset의 특징을 간단하게 추려봤습니다.
1) classification task (숫자)
2) 28 x 28 grayscale의 60,000개의 images
3) flatten 하여 784 dimension의 single sequence를 하나의 data로 feeding
4) apply permutation, breaking locality
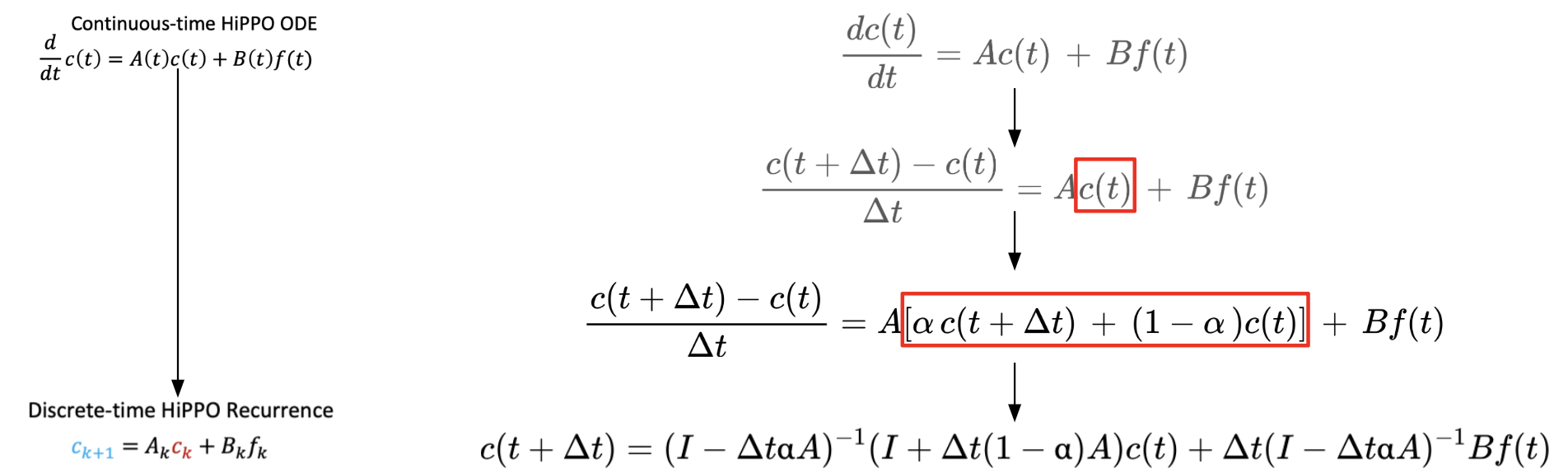
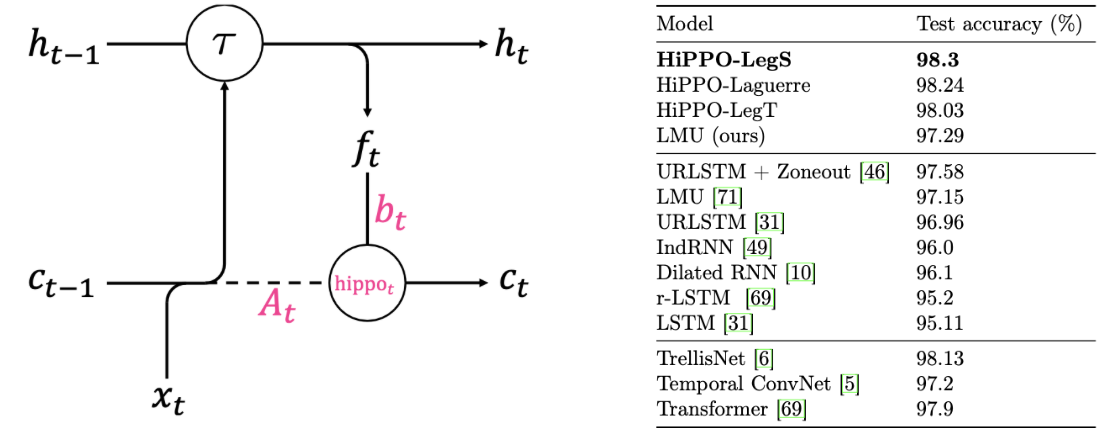
실험시 HiPPO는 위와 같이 RNN(LSTM)의 모듈을 번형시켜 활용을 했습니다. 어떤 모델이든 Hidden dimension은 512로 고정했습니다. 512를 초과하여 Hidden dimension을 증가시켜봤지만 성능이 달라지지 않았다고 합니다. 성능을 HiPPO-LegS, HiPPO-LagT, HiPPO-LegT 순임을 알 수 있는데요. HiPPO-LegS는 state-of-the-art를 달성했습니다. 직관적으로 infinite time을 모두 반영한 HiPPO-LegS, HiPPO-LagT가 성능이 좋음을 관찰할 수 있습니다.
다음 chapter부터는 HiPPO의 미분방정식을 유도하기위한 이론적 배경을 다져보도록하겠습니다.
ODE: from continuous domain To discrete domain
HiPPO의 미분방정식을 유도하기 위해서는 오른쪽 그림과 같이 continuous domain에서 discrete domain으로 전환시켜야합니다. 이때, Generalized Bilinear Transformation를 활용해 discretize 합니다. 오른쪽 그림으로 insight sketch를 나타내봤습니다. α의 값에 따라 다양한 discretization이 결정됩니다.
forward Euler(α = 0), backward Euler(α = 1), bilinear(α = 1/2)
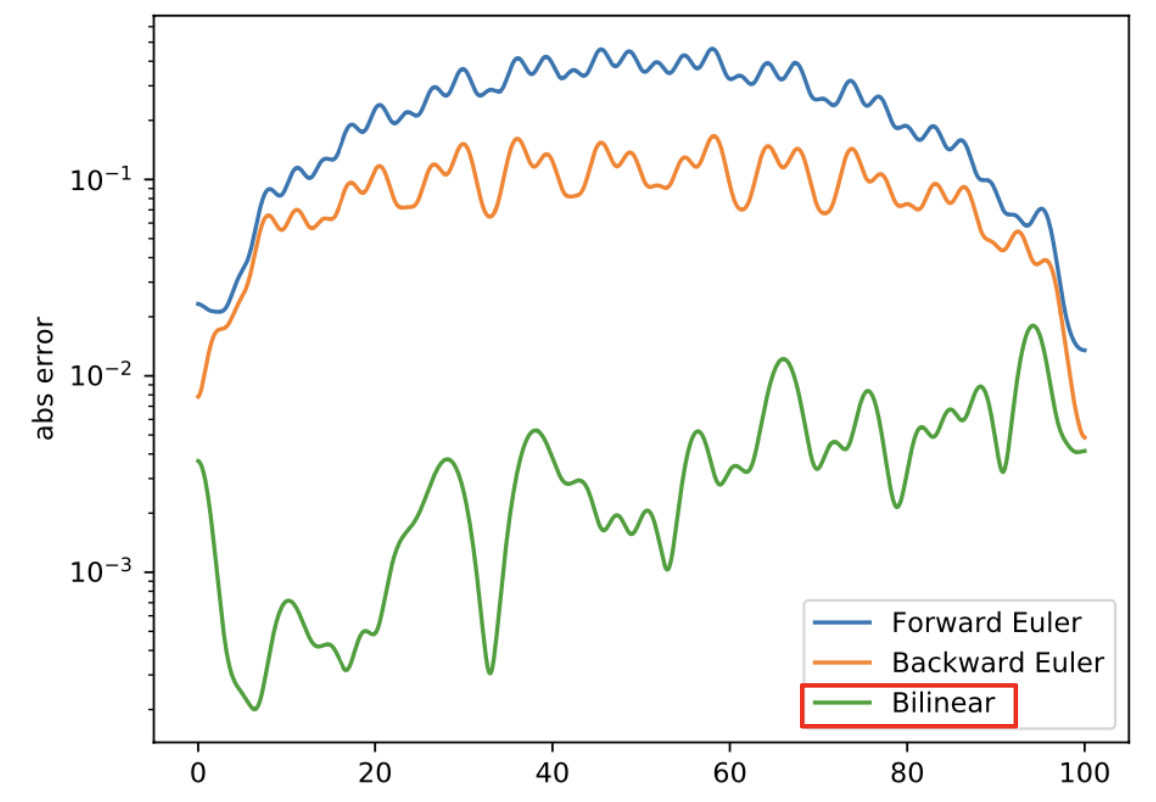
각 방법에 따라 f (x) = 1/4 sin x + 1/2 sin(x/3) + sin(x/7)의 error를 비교한 결과 bilinear discretization이 제일 성능이 좋음을 확인했습니다.
Properties of Legendre Polynomials
Legendre Polynomials는 아래의 방식으로 measure와 basis를 정의합니다.
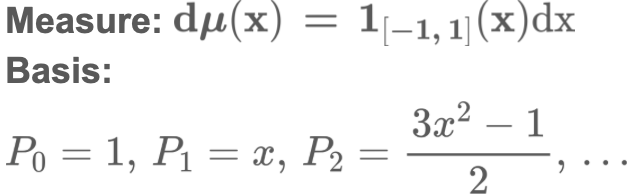
이들은 아래의 equation을 만족합니다.
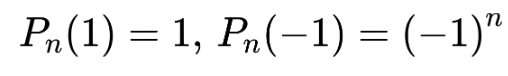
또한, 이들은 아래의 orthogonality를 만족합니다.
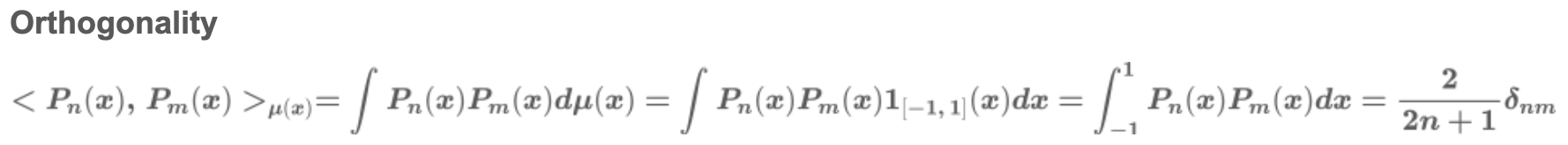
한편, 이들의 관계는 아래의 identity가 존재합니다. 이 성질을 활용해 recurrent property를 얻어낼 수 있습니다.
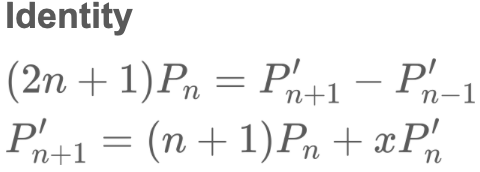
recurrent property는 hippo의 미분방정식을 얻어내는데 핵심적인 역할을 하고 있습니다.
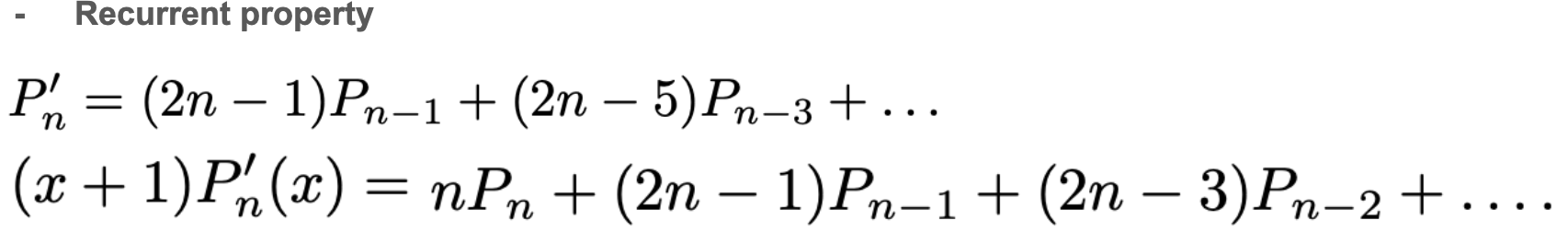
한편, 논문에서 활용하는 LegT(translated legendre)는 위의 measure과 basis를 scaling, transition을 활용해 번형한 형태를 활용합니다!
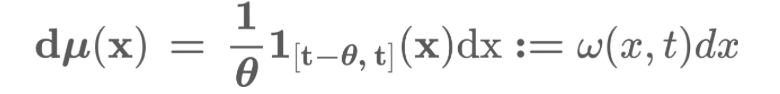
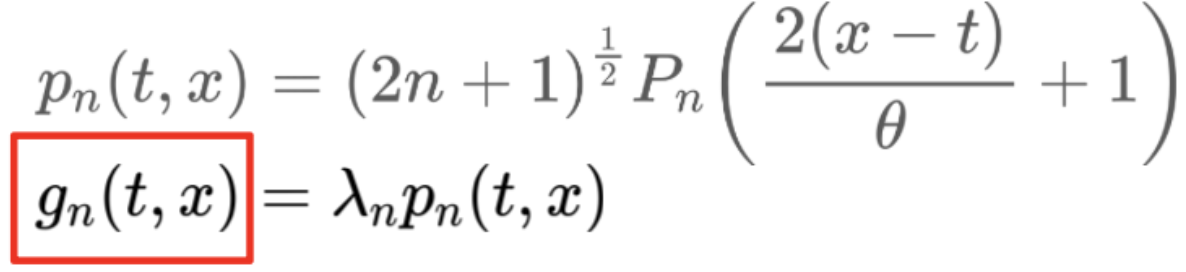
여기서 활용되는 g가 바로 orthogonal polynomial basis set G의 원소를 나타냅니다. lambda가 함께 고려되어 reconstruction 시에 rescaling term이 한번 더 들어가게 됩니다. meausre을 정의할 때, dx 앞의 항을 omega로 치환한 것을 기억해두십시오.
close look: HiPPO-LegT
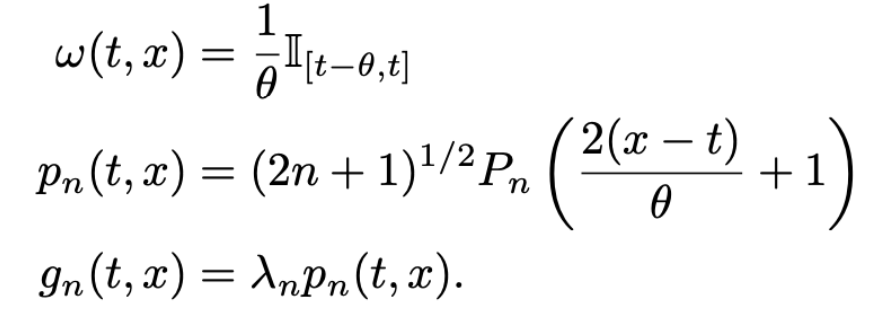
앞의 chapter에서 omega가 그대로 사용되었음을 확인할 수 있습니다. tanslated legendre라는 이름에 걸맞는 것을 볼 수 있죠.
g는 legendre polynomial의 특성을 그대로 이어받아 아래의 특징 역시 만족합니다.
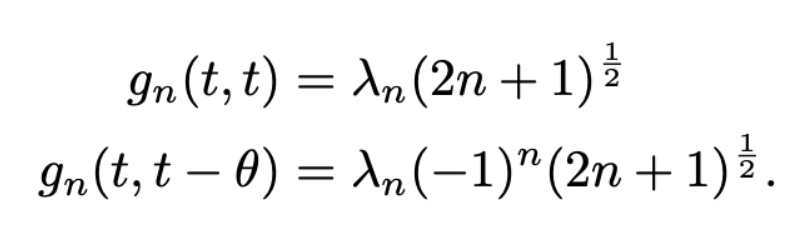
이때, c(t)를 미분하면 일련의 식을 만족하며 앞에서 줄곧 말해왔던 미분 방정식이 등장하게 됩니다. 디테일은 슬라이드에 표기했습니다.


glimpse: HiPPO-LagT & HiPPO-LegS
HiPPO-LagT
HiPPO-LegS
마찬가지로 measure과 basis를 정의한뒤 recurrence property + approximation을 활용해 미분방정식을 이끌어낼 수 있습니다.
3. 마치며
다소 ML, DL과 멀어진 느낌이 없잖아 있는데요. 이렇게 fundamental한 구조로 sota를 달성해냈다는게 근본이 있어보이네요. 결국 basic이 중요함을 다시금 깨닫는 주 였습니다.
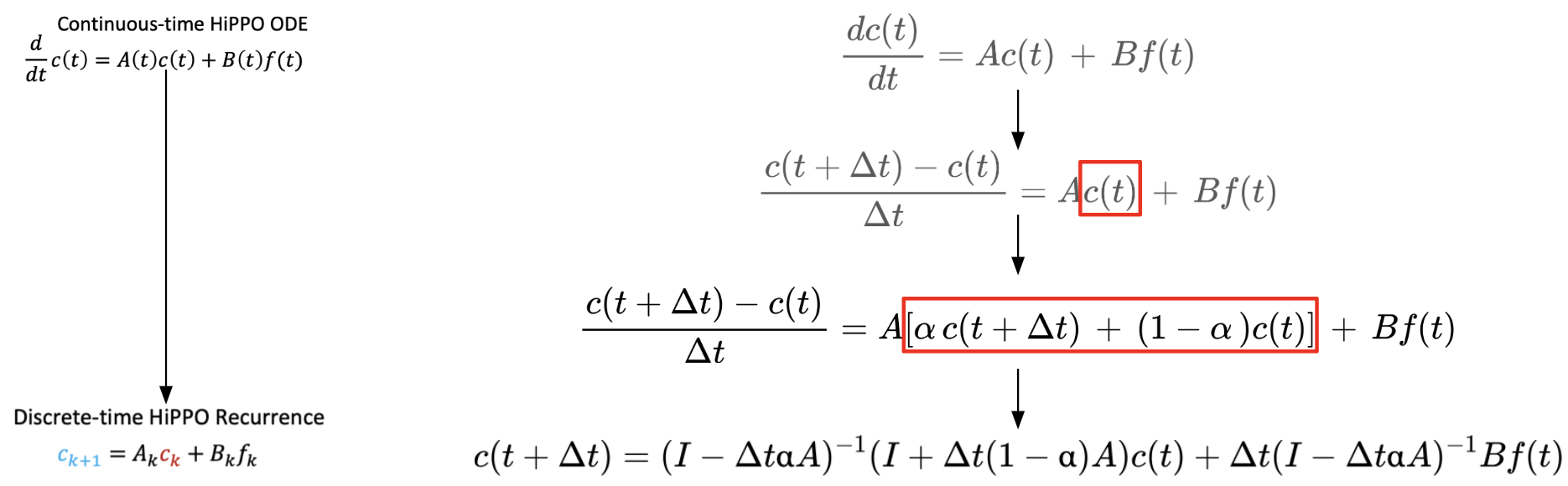
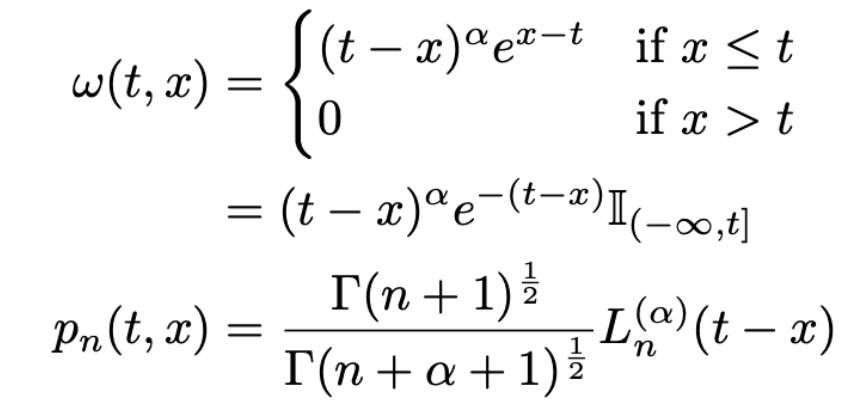

감사합니다 이해에 큰 도움이 되었습니다.