시작하며
벌써 7월 3주차입니다.
최근에 convex optimization에 관련된 책을 학교 도서관에서 빌려 읽었습니다.
convex programming에서 Local optimum은 Global optimum이다!

아무튼, 요즘은 아래의 것들을 진행하고 있습니다. 특히, FIM_SNU의 과제를 진행하려면 statistics에 관련된 내용을 익혀야합니다. 그래서 고생을 좀 하고 있습니다. 관련해서 자료조사를 하며 알게된 내용을 간단하게 review 하고자 합니다.
- 서울대 포스코 수영장 아침 강습 (08:00 ~ 09:00), 놀이터 턱걸이
- AIIS CIC (AI 연구원 산학협력센터) 인턴
- 2023 Fastmri challenge 조교
- 빅데이터 기반 금융투자모형 연구(FIM_SNU) 교육 프로그램
- Study: convex optimization, time series analysis 등
1. Bayesian vs Frequentist
Bayesian와 Frequentist는 두 가지 다른 통계적 접근법을 나타내는 용어입니다. 이들은 아래의 두 관점에서 차이점이 있습니다.
a. 통계 추론에 접근하는 방식
b. 불확실성을 다루는 방법
Bayesian Statisticians
Bayesian은 불확실성을 확률의 개념으로 환원하고, 사전 지식과 관측 데이터가 결합된 정보를 얻으려고 합니다. 모집단 파라미터에 대해 확률 분포를 가정하고, 관측 데이터를 통해 사후 확률 분포를 계산하여 파라미터에 대한 추정치와 불확실성을 파악합니다.
Bayesian Theorem은 아래와 같이 나타낼 수 있습니다.
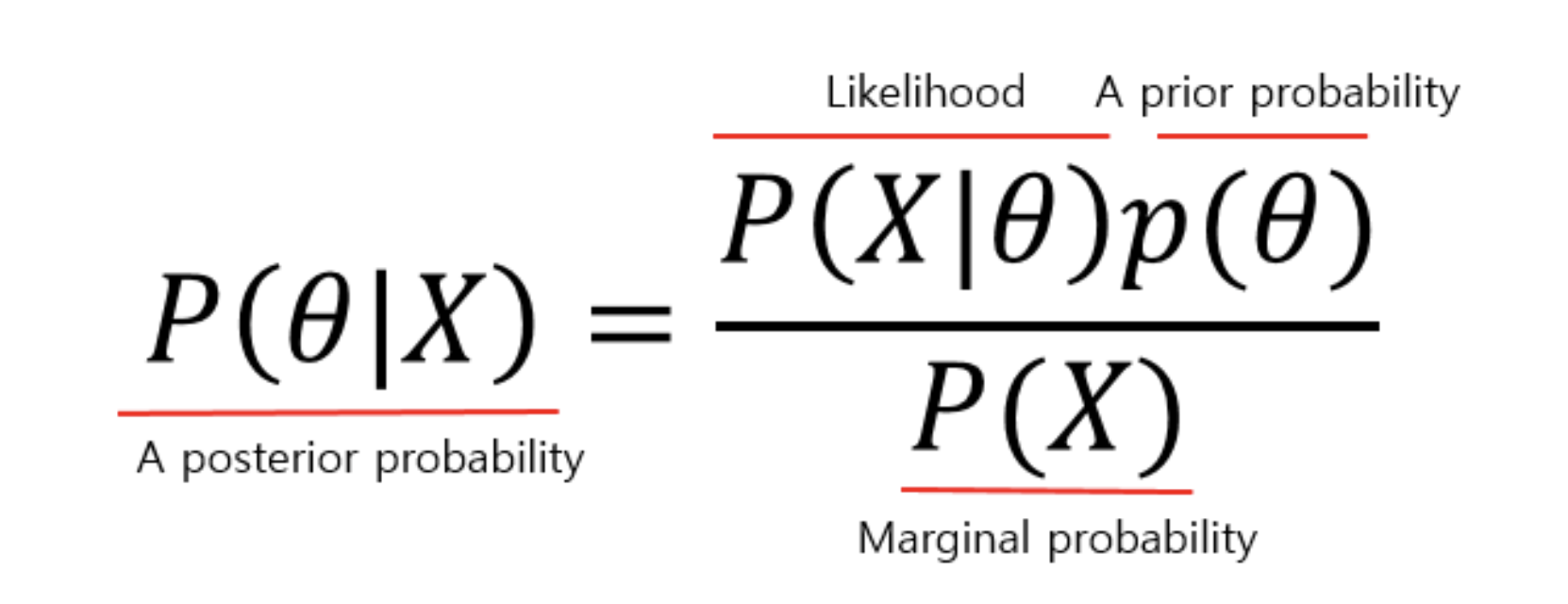
사전 분포(prior): 선험적으로 주어진 파라미터에 대한 믿음의 정도
사후 분포(posterior): 사전 분포와 관측 데이터의 결합으로 얻어지는 파라미터에 대한 믿음의 정도
추론과 가설 검정은 사후 확률 분포를 사용하여 수행되며, 결과는 주어진 데이터에 대한 "확률적 해석"을 제공합니다.
Frequentist Statisticians
Frequentist는 관측 데이터를 바탕으로 모집단의 불확실성에 대한 정보를 얻으려고 합니다. 모집단 파라미터(평균, 분산 등)를 고정된 값으로 가정하고, 이러한 파라미터 값을 추정하는 데 집중합니다.샘플링을 통해 얻은 데이터를 사용하여 점추정 및 신뢰구간 등을 계산하여 "모집단 파라미터에 대한 추정치와 불확실성"을 파악합니다. 가설 검정을 통해 주어진 데이터에 대한 근거를 평가하고, 귀무가설을 기각하거나 기각하지 않음으로써 통계적 결론을 내립니다.
점추정(Point estimation): 통계학에서 모집단의 파라미터를 하나의 값으로 추정하는 방법을 말합니다. 모집단 파라미터는 모집단의 특성을 나타내는데 사용되며, 일반적으로 모집단 전체를 조사하는 것은 현실적으로 어렵거나 비용이 많이 들기 때문에 표본 데이터를 사용하여 추정합니다.
귀무가설(null hypothesis): 가설 검정은 귀무가설을 기각 또는 채택하는 과정으로 이루어지며, 주어진 데이터에 대해 귀무가설이 기각될 경우 대립가설을 받아들이게 됩니다. 대립가설은 일반적으로 연구자가 증명하고자 하는 가설로, 귀무가설의 반대되는 내용을 나타냅니다.
2. Fisher’s p-values
Fisher's p-value는 가설 검정 중 하나로 귀무가설을 평가하는 데 사용되는 값입니다. Fisher's p-value는 데이터로부터 얻은 통계량이 귀무가설 하에서 얼마나 극단적인지를 나타내는 확률입니다. p-value는 유의성의 크기만을 나타내며, 효과 크기나 실제 의미에 대한 정보는 주지 않습니다.
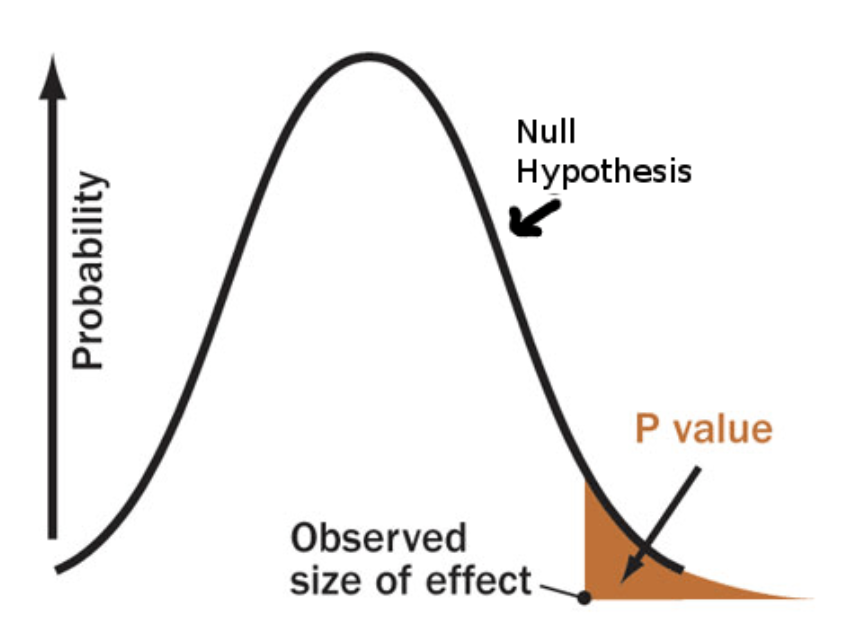
가설 검정에서 Fisher's p-value는 다음과 같은 과정을 거칩니다:
a. 귀무가설(H0)과 대립가설(H1) 설정
b. 표본 데이터 수집
c. 통계량 계산
d. Fisher's p-value 계산: 귀무가설 하에서, 현재 얻은 통계량과 같거나 더 극단적인 값이 나올 확률을 계산하는 것입니다.
d. p-value 해석: 계산된 p-value을 사전에 정한 유의수준(보통 0.05)과 비교하여, p-값이 유의수준보다 작으면 귀무가설을 기각하고 대립가설을 채택합니다. 그렇지 않으면 귀무가설을 채택합니다.
p-value 계산은 통계 소프트웨어를 사용하거나, 통계 패키지(R, Python 등)의 함수를 활용하여 수행할 수 있습니다. 통계 패키지는 주어진 데이터와 검정 방법에 따라 p-값을 자동으로 계산해주므로, 일반적으로 수동으로 계산할 필요는 없습니다.
3. t-test
t-test는 두 그룹의 평균이 서로 다른지를 비교하는데 사용되는 통계적인 방법입니다. 특히, 두 독립적인 그룹 간의 평균 차이에 대한 가설 검정에 주로 사용됩니다. t-test는 표본 데이터를 사용하여 두 그룹의 평균에 대한 추정치와 그 차이의 유의성을 확인하는데 유용합니다.
일반적으로 두 가지 유형의 t-test가 있습니다:
독립 표본 t-test (Independent Samples t-test):
두 개의 독립적인 그룹(예: 실험 그룹과 대조 그룹)의 평균을 비교하는데 사용됩니다. 각 그룹은 서로 독립적이며, 하나의 그룹의 데이터는 다른 그룹의 데이터와 관련이 없습니다. 등분산 가정을 만족하면 등분산 t-test를 사용하고, 만족하지 않으면 등분산을 가정하지 않는 Welch's t-test를 사용합니다.
대응 표본 t-test (Paired Samples t-test):
하나의 그룹에서 동일한 사람 또는 대상체를 두 번 측정한 경우에 사용됩니다. 두 관측값 간의 차이에 대한 평균을 비교하는데 사용되며, 대응 표본 t-test는 해당 차이의 유의성을 확인합니다.
t-test를 수행하려면 다음 단계를 따릅니다:
a. 귀무가설(H0)과 대립가설(H1) 설정
b. 표본 데이터 수집
c. t-값 계산: 두 그룹의 평균과 표준편차를 사용하여 t-값을 계산합니다.
d. p-값 계산: t-값과 자유도(degree of freedom)를 사용하여 p-값을 계산합니다.
e. 결과 해석: p-값을 사전에 정한 유의수준(보통 0.05)과 비교하여, p-값이 유의수준보다 작으면 귀무가설을 기각하고 대립가설을 채택합니다. 그렇지 않으면 귀무가설을 채택합니다.
t-test는 평균 비교를 위한 간단하고 효과적인 방법으로 널리 사용되며, 데이터 간의 유의미한 차이를 평가하는데 도움이 됩니다.
4. Neyman-Pearson’s framework
Neyman-Pearson의 검정 방법은 통계적 가설 검정에 사용되는 통계학의 기본적인 프레임워크 중 하나입니다. 이 방법은 가설 검정을 할 때 두 가지 가설을 설정하고, 그 중 하나를 검증하는데 초점을 맞춥니다. 이 두 가설은 다음과 같이 정의됩니다:
귀무가설 (H0, Null Hypothesis): 기본적인 가설로, 아무런 효과 또는 차이가 없다고 가정합니다. 일반적으로 검증하고자 하는 가설입니다.
대립가설 (H1, Alternative Hypothesis): 귀무가설의 반대되는 가설로, 특정 효과 또는 차이가 있다고 가정합니다. 검증하고자 하는 가설입니다.
Neyman-Pearson의 검정 방법에서 주요 목표는 귀무가설을 기각 또는 채택하는 것입니다. 이때, 가설 검정은 두 가지 오류를 고려하여 진행됩니다:
제 1종 오류(Type I Error): 귀무가설이 참인데도, 잘못하여 귀무가설을 기각하는 오류입니다. 이 오류는 일반적으로 유의수준(alpha)로 정의되며, 유의수준은 주로 0.05로 설정됩니다.
제 2종 오류(Type II Error): 귀무가설이 거짓인데도, 잘못하여 귀무가설을 채택하는 오류입니다. 이 오류는 대립가설을 검정하는 과정에서 발생할 수 있습니다.
Neyman-Pearson의 방법은 다음과 같은 특징을 가집니다:
검정을 할 때, 귀무가설을 거부하는 기준을 설정합니다. 이 기준은 유의수준과 관련되며, 일반적으로 p-값과 비교하여 결정합니다. 검정 결과에 대한 해석은 주로 기각 여부를 통해 이루어지며, 기각되면 대립가설을 지지하는 근거가 된다고 볼 수 있습니다. Neyman-Pearson의 방법은 특히 검정의 엄격성과 민감성을 강조합니다. 즉, 제 1종 오류를 최소화하고, 제 2종 오류를 가능한 한 줄이려고 합니다. Neyman-Pearson의 검정 방법은 통계적인 가설 검정에서 가장 일반적으로 사용되는 프레임워크 중 하나로, 가설 검정 결과를 합리적으로 평가하고 결정하는데 도움을 줍니다.
5. OLS (Ordinary Least Square) summary 해석
통계학 관련 domain에서 아래와 같은 result 형식의 summary를 자주 볼 수 있습니다. 이를 해석하는 방식을 간단하게 정리하기 위해 아래의 두 글을 참고했습니다.
a. Interpreting the results of Linear Regression using OLS Summary
b. Statistics: How Should I interpret results of OLS?
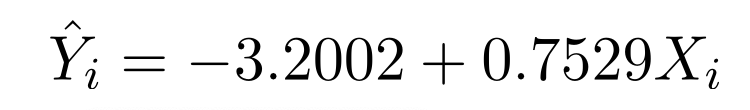
아래의 results는 위의 regression의 결과를 분석한 것입니다. 각각의 항목에 대해서 살펴보겠습니다.
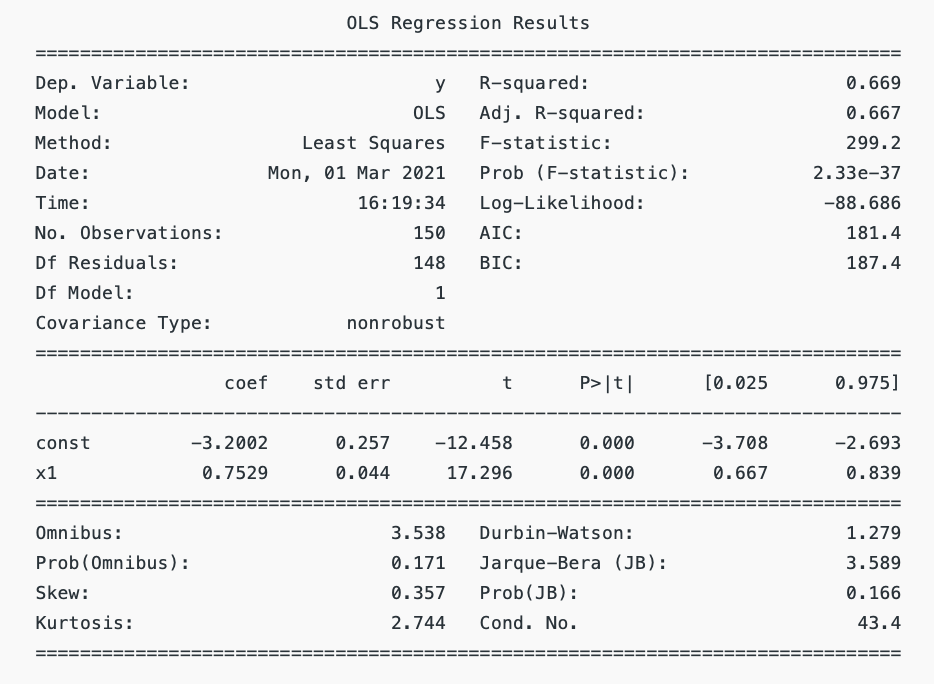
Dep. variable
Dependent variable는 다른 변수에 의존적적인 변수입니다. 이 회귀 모델에서는 Y가 Dependent variable이므로 X가 Y에 어떤 영향을 미치고 있는지에 대해 관심이 있습니다.
Model, Method
다양한 통계적 모델과 방법론이 있지만, 여기선 OLS와 Least squares 방식의 최적화 기법을 사용해 fitting을 진행한 것을 알 수 있습니다.
No. Observations, Df Residuals, Df Model
No. Observations는 샘플의 사이즈, Df Model은 모델에 활용된 independent variable의 개수를 나타내고 있습니다. 이때, Df Residuals과 Df Model 그리고 1을 전부 더해주면 No. Observations와 같아집니다.
Covariance type
robust 회귀는 outlier나 비정상적인 데이터에 덜 민감하도록 설계된 방법으로, 이상치 등에 더 robust한 회귀 계수 추정을 제공합니다. 반면에 기본적인 OLS에서 사용되는 Nonrobust은 이상치 등에 덜 견고하며, 이러한 데이터의 영향을 크게 받을 수 있습니다.
R-squared, Adj. R-squared
독립 변수에 의해 설명되는 종속 변수의 변동 비율을 나타내는 것을 의미하는 R-squared는 회귀분석에서 사용되는 통계적 지표입니다. R-squared의 최대 가능 값은 1로, 이 값이 클수록 회귀 모델이 더 좋은 설명력을 가진다는 것을 의미합니다.
하지만, R-squared 값은 종속 변수의 수가 증가함에 따라 증가하게 되는데, 이로 인해 회귀 모델의 예측력에 추가적인 독립 변수가 기여하는지를 판단하는 데 있어서 결정적인 정보를 제공하지 못할 수 있습니다.
위 문제를 해결하기 위해 Adj. R-squared이 등장했습니다. 이 값은 오직 추가적인 변수가 회귀 모델의 설명력에 기여할 때에만 증가합니다.
F-statistics, Prob(F-statistics)
F-statistics는 회귀분석에서 전체 모형의 적합도를 평가하는 데 사용되는 통계량입니다. 회귀분석은 독립 변수들이 종속 변수의 변동을 얼마나 잘 설명하는지를 알아보는 것인데, F-statistics는 모델이 종속 변수에 대해 유의미한 설명력을 가지는지 여부를 검정하는 데에 쓰입니다.
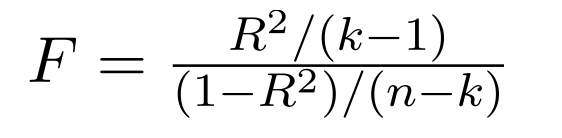
F-statistics는 회귀 모델의 설명력과 오차의 분산 간의 비율을 계산하여 구합니다. 모델의 설명력이 높고, 오차의 분산이 상대적으로 작을수록 F-statistics는 큰 값을 가지게 됩니다. 이 때, F-statistics는 유의한 값이라면, 적어도 하나 이상의 독립 변수가 종속 변수에 대해 통계적으로 유의미한 영향을 가지고 있다는 것을 의미합니다.
Prob(F-statistics)는 F-통계량의 유의확률(p-value)을 나타내는 값입니다. F-statistics이 가질 수 있는 분포에서의 F-statistics 값과 실제 F-statistics 값 사이의 확률을 측정합니다. 유의확률은 모델의 설명력이 우연히 발생한 것인지 아니면 실제로 의미 있는 것인지를 판단하는 데에 사용됩니다. 일반적으로 유의확률이 작을수록(일반적으로 0.05 이하), F-statistics이 유의미하다고 판단됩니다.
Log-likelihood
Log-likelihood는 확률적인 모델에서 주어진 데이터에 대한 likelihood를 로그 변환한 값입니다. Maximum Likelihood Estimation을 사용할 때, Log-likelihood를 최대화하는 방향으로 모델의 파라미터를 추정합니다.
likelihood는 주어진 데이터가 모델에 얼마나 적합한지를 나타내는 값으로 높을수록 모델이 데이터를 잘 설명한다고 해석할 수 있습니다.
AIC, BIC
AIC(아카이케 정보 기준)와 BIC(베이지안 정보 기준)은 모델 선택에 사용되는 지표입니다. AIC나 BIC를 적절하게 사용하여 적절한 모델을 선택하는 것이 중요합니다.
AIC는 새로운 변수가 회귀 방정식에 추가될 경우 모델 내 오류를 패널티로 주는 모델 선택 기준입니다. 전체 모델의 파라미터의 수에서 likelihood를 빼서 계산됩니다. AIC는 가능한 모델들을 비교할 때 사용되며, 작은 값일수록 더 나은 모델이라고 간주됩니다. AIC는 모델의 복잡성을 반영하면서도 데이터에 잘 적합되는 모델을 선호합니다.
BIC는 AIC의 변형으로, 패널티를 더 강화하여 더욱 더 간단한 모델을 선호하는 특징이 있습니다. BIC는 AIC와 마찬가지로 가능한 모델들을 비교하여 사용되며, AIC보다 더 큰 패널티를 적용하여 overfitting을 방지합니다. BIC는 모델의 복잡성에 대해 더욱 엄격하게 평가하며, 데이터에 더 일반화된 모델을 선택하도록 도와줍니다.
coef, std err, t, P>|t| 등
coef는 각 independent 항들에 대응되는 상수(beta)입니다. 이들의 standard error은 아래와 같은 수식으로 표현가능하고 이들을 results에서 확인할 수 있습니다. 여기서, σ-squared는 Residual Sum Of Square입니다.
a. std err(intercept term)
b. std err(coefficient term)
t는 t-test에서의 t-value를 나타냅니다. coefficient term에 대한 t-test를 예로 들어보겠습니다. 아래와 같이 귀무가설과 대립가설을 설정할 수 있습니다. t-value와 자유도를 활용해 p-value를 계산할 수 있고 이를 통해 귀무가설을 기각할지에 대한 사안이 결정됩니다. p-value가 충분히 작으면(0.05) 귀무가설을 기각하고 대립가설을 채택합니다.

Omnibus, Prob(Omnibus)
OLS의 가정 중 하나는 residuals이 정규 분포를 따른다는 것입니다. 이를 확인하기 위해 Omnibus 테스트를 수행합니다. 여기서 귀무 가설은 오차 항이 정규 분포를 따른다는 것입니다. Prob(Omnibus) 값이 1에 가까울수록 OLS 가정이 만족되었다고 볼 수 있습니다. Prob(Omnibus) 값이 작아 OLS 가정이 만족되지 않을 경우, 추정된 계수들은 Best Linear Unbiased Estimators(BLUE)가 아닐 수 있습니다.
Durbin-Watson
Durbin-Watson 통계량은 OLS의 또 다른 가정인 등분산성(homoscedasticity)을 평가하는 데 사용되는 지표입니다. 이는 오차 항의 분산이 일정하다는 것을 의미합니다. Durbin-Watson 통계량은 보통 1부터 2 사이의 값을 가지며, 이 구간에서 값이 가까울수록 바람직합니다.
Jarque-Bera (JB), Prob(JB), Skew, Kurtosis
Jarque-Bera(JB) 검정은 회귀분석에서 residuals(잔차)의 정규성 가정을 평가하는데 사용되는 통계적인 검정 방법입니다. 이 검정은 오차 항의 skewness와 kurtosis에 기초하여 정규 분포에서 기대되는 값과의 차이를 비교합니다.
Skewness는 데이터의 분포가 좌우 대칭인 정규 분포와 얼마나 차이나는지를 나타내는 지표입니다. 왜도가 0이면 데이터가 정규 분포와 유사한 형태를 가지며, 양수면 오른쪽으로 꼬리가 긴 분포, 음수면 왼쪽으로 꼬리가 긴 분포를 의미합니다.
Kurtosis는 데이터의 분포가 정규 분포보다 얼마나 뾰족한지를 나타내는 지표입니다. 첨도가 0이면 데이터가 정규 분포와 유사한 형태를 가지며, 양수면 뾰족한 형태, 음수면 완만한 형태를 의미합니다.
JB 검정은 왜도와 첨도를 바탕으로 잔차의 정규성을 평가하는데, 대략적으로 정규 분포를 따르는 경우 JB 검정의 통계량은 대략적으로 0에 가까운 값을 갖게 됩니다.
Prob(JB)는 JB 검정의 p-value을 의미합니다. 유의확률은 오차 항의 정규성에 대한 귀무 가설이 참일 확률로, 유의확률이 작을수록(일반적으로 0.05 이하) 귀무 가설을 기각하게 됩니다. 따라서 Prob(JB)가 작은 값이면, 오차 항의 정규성 가정이 만족되지 않는다고 할 수 있습니다.
Cond. No.
Condition Number(조건수)는 회귀분석에서 다중공선성(multicollinearity)을 평가하는데 사용되는 지표입니다. 다중공선성은 독립 변수들 간에 강한 선형 관계가 존재하는 경우를 의미하며, 이는 회귀 모델의 해석과 예측에 영향을 미칠 수 있습니다.
조건수는 회귀 모델에서 독립 변수들의 표준화된 편차와 상관관계의 비율로 정의됩니다. 일반적으로 조건수가 30 이하라면 다중공선성이 크게 문제되지 않으며, 조건수가 100 이상일 경우 다중공선성이 심각한 문제가 될 수 있습니다.
따라서 조건수를 통해 회귀 모델의 다중공선성을 평가하고, 다중공선성이 높을 경우에는 변수 선택, 변수 변환 등의 방법을 사용하여 문제를 해결하거나 회귀 모델을 개선하는 노력이 필요합니다. 적절한 변수 선택과 전처리를 통해 다중공선성을 최소화하여 더 정확하고 신뢰성 있는 회귀 모델을 구축할 수 있습니다.
마치며
당분간은 아래의 것들에 집중해 볼 계획입니다.
- convex optimization review
- optimal control
- combinatorial optimization
- reinforcement learning
- statistics: financial analysis
- predictive AI models for financial domain
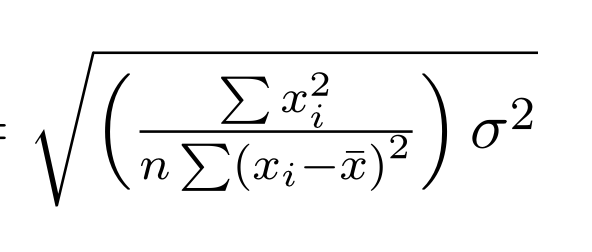
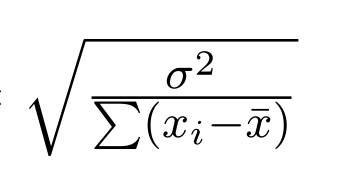


유익한 정보를 제공해주셔서 감사합니다.