시작하며,

저번 글에서는 Coherent Point Drift의 사전지식인 EM을 살펴보았습니다. 한편, CPD의 E step, M step을 유도하는 과정에서 특수한 optimal problem이 등장하는데요. 이번엔 그것!에 대해서 다뤄보려고 합니다. 이름하여~! closed-form solution to the maximization of tr(ATR) 입니다. 논문의 제목은 On the closed-form solution of the rotation matrix arising in computer vision problems입니다. 이를 톺아보기 위한 Singular Value Decomposition과 trace의 간략한 속성에 대해서 배경지식으로 이야기해보려고 합니다. 그 뒤에 paper review를 하며 논문에서 주장하는 optimization 문제의 해를 어떻게 구하는지 소개해보겠습니다.

논문 주소: https://arxiv.org/pdf/0904.1613.pdf

Prior knowledge

1. Singular Value Decomposition (SVD)

선형대수학의 꽃이라고도 할 수 있는 Singular Value Decomposition은 임의의 행렬 A를 $U, \Sigma , V$로 분해하는 것을 목표로 합니다. A는 $m × n$ matrix 라고 생각합니다. 결론부터 이야기하면 아래와 같습니다. 차근차근 $U, r, \Sigma, V$에 대해서 알아보겠습니다.

$A = U \Sigma V^T$
U: $m × m$ orthonormal matrix
$\Sigma$: $m × n$ matrix with $r$ singular values (0 is not included in singular values)
V: $n × n$ orthonormal matrix

spectral decomposition의 속성을 참조하면 $A^T A$는 $n × n$ 대칭 행렬이므로 $n$개의 직교하는 고유벡터가 존재합니다. 이를 $v_1, v_2, ..., v_n$이라고 해봅니다. 이들은 각각 고유값 $\lambda_1, \lambda_2, ..., \lambda_n$에 대응됩니다. $\lambda_1 \geq \lambda_2 \geq ...\geq \lambda_n$의 순서룰 만족합니다.

$A^TAv_i=\lambda_iv_i, \space i=1,2,...,n$

여기서 잠깐!
$\lambda_i, \space i=1,2,...,n$ 중 0이 아닌 값을 가지는 $\lambda_i$의 개수를 $r$라고 생각합니다!
즉, $\lambda_i=0, \space i=r+1,r+2,...,n$

위를 참고하여 singular value $\sigma$를 다음과 같이 정의합니다.

$\sigma_i = \sqrt {\lambda_i}, \space i=1,2,...,r$

선형 변환 $L(X) = AX$를 통해 $A^T A$의 기저 {$v_1, v_2, ..., v_n$}를 선형 변환시키면 {$Av_1, Av_2, ..., Av_r$}을 얻을 수 있습니다. 고윳값이 0인 것에 대응되는 기저는 전부 0 벡터가 되므로 기저로 고려하지 않습니다. {$Av_1, Av_2, ..., Av_r$}의 element의 내적을 생각해봅시다.

$<Av_i, Av_j> = (Av_i)^TAv_j = v_i^TA^TAv_j = \lambda_jv_i^Tv_j$

$A^T A$의 기저는 orthonormal basis이므로 아래가 성립합니다.

$<Av_i, Av_j> = \lambda_i$ if $i = j$
$<Av_i, Av_j> = 0$ if $i \ne j$

따라서, {$Av_1, Av_2, ..., Av_r$}은 singular value $\sigma$를 활용해 아래와 같이 normalization을 진행하고 $u$로 치환 해보겠습니다.

{$Av_1/\sigma_1, Av_2/\sigma_2, ..., Av_r/\sigma_r$} = {$u_1$, $u_2$, ..., $u_r$}

이를 종합하여 생각해보면 다음이 성립합니다.

$A\begin{pmatrix} v_1 \space v_2 \space ... v_n\end{pmatrix} = \begin{pmatrix} Av_1 \space Av_2 \space ... Av_n\end{pmatrix} = \begin{pmatrix} \sigma_1 u_1 \space \sigma_2 u_2 \space ... \space \sigma_r u_r \space 0 \space ... \space 0 \end{pmatrix} = \begin{pmatrix} u_1 \space u_2 \space ... \space u_r \space 0 \space ... \space 0 \end{pmatrix} \begin{pmatrix}\sigma_1 \space ... \space ... \space 0\\ 0 \space \sigma_2 \space ... \space \space 0 \\ \space ... \space ... \space \space\\ .. \space \sigma_r \space ... 0 \\ 0 \space ... \space ... \space 0\\ \space ... \space ... \space \space\\ 0 \space ... \space ... \space 0\end{pmatrix}$

위의 $\begin{pmatrix} u_1 \space u_2 \space ... \space u_r \space 0 \space ... \space 0 \end{pmatrix}$을 m개의 basis가 되게끔 확장해주면 아래와 같은 SVD를 얻을 수 있습니다.

$AV = U \Sigma$
$A = U \Sigma V^T$
$V = \begin{pmatrix} v_1 \space v_2 \space ... v_n\end{pmatrix}$
$U = \begin{pmatrix} u_1 \space u_2 \space ... u_m\end{pmatrix}$
$\Sigma = \begin{pmatrix}\sigma_1 \space ... \space ... \space 0\\ 0 \space \sigma_2 \space ... \space \space 0 \\ \space ... \space ... \space \space\\ .. \space \sigma_r \space ... 0 \\ 0 \space ... \space ... \space 0\\ \space ... \space ... \space \space\\ 0 \space ... \space ... \space 0\end{pmatrix}$

2. properties of trace

$tr(ABC) = tr(BCA)$

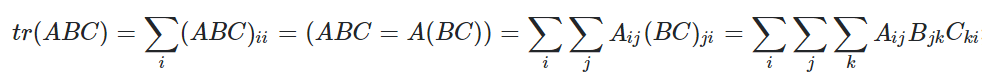
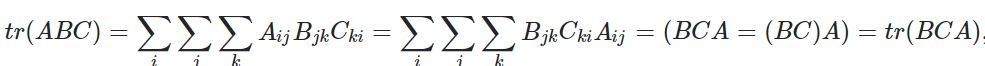
paper review: On the closed-form solution of the rotation matrix arising in computer vision problems

0. Abstract

우리는 주어진 A와 미지의 회전변환 R에 대해서 $tr(A^T R)$을 최대화하기 위한 closed-form 해를 보였습니다. 이 문제는 optimal rotation matrix estimation을 비롯한 computer vision의 문제에서 많이 발생합니다. 우리는 이 문제의 역사적 발전과정과 일반적인 증명을 다룹니다. degenerate A를 고려한 증명이 이 논문의 contribution입니다.

1. Introduction

많은 computer vision 문제는 optimal rotation matrix estimation이 필요합니다.

$max_R \space tr(A^T R), \space s.t \space R^TR=I, det(R) = 1$

Frobenius inner product(element-wise)의 최소화 작업을 거치며 위의 문제를 유도해낼 수 있습니다.

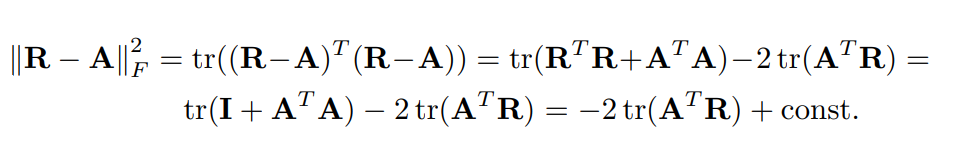
$tr(A^T R)$을 maximize 하는 문제로 환원되는 optimization problem의 리스트를 아래에 나열해봤습니다.

• the closest orthogonal approximation problem

  

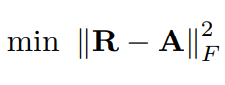
• orthogonal Procrustes problem

  

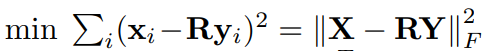
• Absolute orientation problem (generalized Procrustes problem)

  

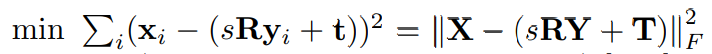
• Scott and Longuet-Higgins correspondence estimation

  

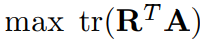
2. The Lemma

$R_{D×D}$를 미지의 rotation matrix, $A_{D×D}$는 주어진 실수 행렬이라고 하자. A의 singular value decomposition은 $USV^T$이다($UU^T = VV^T = I$, $S = d({s_i}), s_1 \geq s_2 \geq ... \geq s_D$). 이때, $tr(A^T R)$을 maximize하는 optimal rotation matrix $R$은 아래와 같다.

$R = UCV^T$, where $C = d(1, 1, . . . , 1, det(UV^T)), \space det(UV^T) = \pm 1$

$R$은 아래의 두개의 경우에 해당하는 A를 제외하고 유일하다:
1. $rank(A) < D − 1$
2. $det(A) < 0$ 그리고 $s_D$ (smallest singular value)가 distinct하지 않을 때 (degenerate)

3. History of the problem

• 1952, Green, full rank를 가지는 positive definite에 대한 orthogonal Procrustes problem의 해를 구함

• 1966, Sch¨onemann, Green의 방식을 일반적으로 확장해 임의의 A에 대해 다루었고 R의 유일성의 토의

• 1981, Hanson and Norris rotation matrix R에 대한 엄격한 증명

• 1955, Fan and Hoffman, polar decomposition의 도입

• 1987, Arun et al., absolute orientation problem 제기

• 1991, Umeyama, optimal strictly rotational matrix에 대한 증명

우리는 Umeyama의 연구를 follow up 했습니다. 우리의 contribution은 불완전했던 Umeyama의 증명을 덧붙였습니다. 세부적으로 degenerate(not-distinct singular values) 한 A의 case를 다뤘습니다.

4. Proof of the Lemma

Lagrange multipliers를 활용해서 constrained problem을 unconstrained problem으로 바꿀 수 있습니다. objective function $f$를 아래와 같이 정의했습니다.

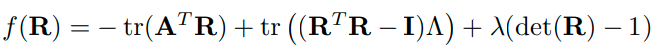
$\lambda, \Lambda$는 모두 unknown Lagrange multiplier 입니다. optimization을 위해 $f(R)$를 $R$에 대해서 편미분하여 0이 되도록하는 값을 구해봅니다.

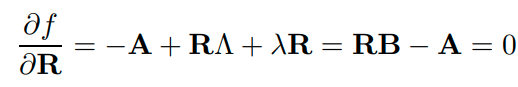
B를 다음처럼 정의해 치환을 해봅니다.

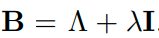
따라서 문제는

을 해결하는 것과 동일합니다.

회전 변환의 성질을 활용하면

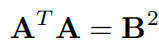
임을 알 수 있습니다.

$B^2$는 symmetric이고 positive definite이므로 spectral decomposition을 진행할 수 있습니다.

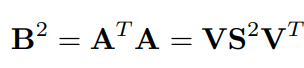
$B^2$의 eigen value는 $s_1^2 \geq s_2^2 \geq ... \geq s_D^2 \geq 0$입니다. ($s_i$는 0 이상의 값) $S$는 음이 아닌 실수 matrix입니다. $S$는 $A$의 singular value를 원소로 가지는 대각행렬입니다.

위의 식을 활용해서 B의 spectral decomposition도 생각해볼 수 있습니다.

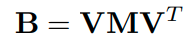
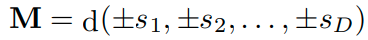
A가 degenerate case ($A^nx= \lambda x$ 이지만 $Ax \ne \lambda x$ 인 경우, 단, $x \ne 0$)인 경우 M이 diagonal matrix가 아닐 수도 있습니다(jordan matrix 참고). 이때의 M은 대칭적인 symmetric block diagonal 구조를 가집니다. block의 개수는 distinct 한 $S^2$의 원소와 같습니다.

다음 3가지 case에 대해서 나눠서 생각해보려고 합니다.

1) non-singular, non-degenerative $A$
2) non-singular, degenerative $A$
3) singular $A$

1) non-singular, non-degenerative $A$
$M$은 diagonal입니다. 아래와 같이 equality와 trace property를 활용하면 다음과 같습니다.

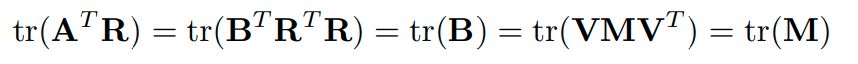
또, 아래의 식을 활용해 $A, M$의 determinant의 sign이 같다는 것을 알 수 있습니다.

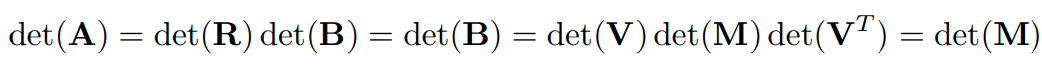
따라서 objective function을 최소화하기 위해서 tr(M)을 최대화해야 합니다. 한편, $A, M$의 determinant의 sign이 같다는 성질을 활용해서 아래와 같이 $M$을 설정할 수 있습니다. ($det(A)$가 음수일 때는 가장 작은 값만 음수로 flip 해줘야 합이 maximize 된다는 직관을 활용 한 것 같습니다.)

objective function은 아래의 optimum value를 가집니다.

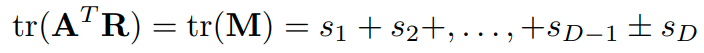
이젠 $R$로 focus를 바꿔봅니다. 아래의 식을 생각해볼 수 있습니다.

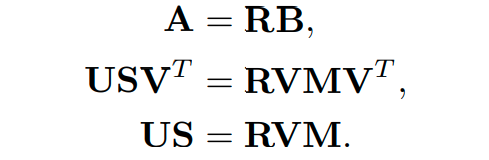
$A$가 non-singular이므로 M은 invertable입니다. 따라서 아래와 같은 unique R을 구할 수 있습니다.

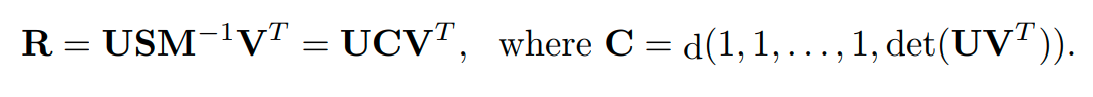
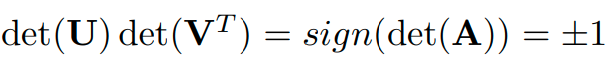
2) non-singular, degenerative $A$
M은 symmetric block diagonal matrix입니다. M이 symmetric matrix이므로 spectral decomposition을 진행 할 수 있습니다. Q는 orthogonal이고 M과 마찬가지로 block-diagonal입니다. (M을 block-wise하게 쪼개서 각각을 spectral decomposition을 진행하고 concatenation을 했다고 생각하면 편합니다.)

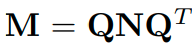
따라서, 아래의 식이 성립합니다.

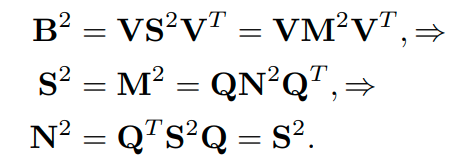
마지막 equality가 성립하는 이유는 $Q$가 block-diagonal이기 때문입니다. block-wise하게 S를 살펴보면 identity matrix의 상수 배가 되는 것이고 거기에 대응되는 Q의 column vector 역시 block의 size 개수만큼 하나의 eigen value에 대응되는 벡터들을 가진다는 것을 생각하면 편합니다. 따라서 아래의 N이 optimal solution이 됨을 알 수 있습니다.

이때, objective function은 아래의 optimum을 가집니다.

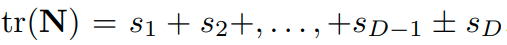
이제, optimal choice N에 대해 M이 어떤 형태를 가질지에 대해 생각해봅시다. $det(A)$의 부호에 따라 나누어 생각해봅니다.

• $det(A)$ > 0
  
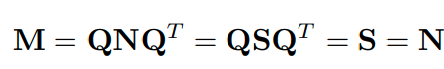
  이때의 M은 유일(unique)합니다.

• $det(A)$ < 0
  $s_D$에서 repeat이 발생하지 않을 경우, 위의 증명에서와 똑같은 과정을 거쳐 $QNQ^T = N$임을 알아낼 수 있습니다.
  $s_D$에서 repeat이 발생할 경우, M이 유일하지 않으므로 위와 같은 방법으로 문제를 해결할 수 없습니다. 이 경우에는 M을 아래와 같이 diagonal 하게 잡아서 증명을 전개합니다.
  
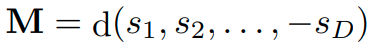
  non-degenerative case와 비슷하게 아래의 식을 만족합니다.
  
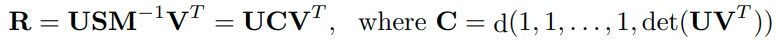
  하지만, 이때는 A의 singular value가 distinct하지 않으므로 A의 SVD가 unique하지 않습니다. 왜냐하면 하나의 singular value에 대응되는 singular vector의 linear combination도 singular vector가 되기 때문입니다.
  아래의 식을 살펴봅시다.
  
  

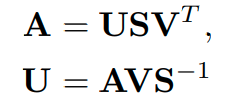
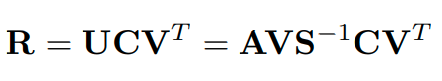
$det(A) > 0$일때, V가 unique하지 않더라도 R은 unique함을 알 수 있는데 그 이유는 $VS^{−1}V^T$가 unique하기 때문입니다. $det(A) < 0$일때는 C가 cancel되지 않아 R이 unique하게 결정되지 않음을 알 수 있습니다.

참고로, Umeyama의 lemma 유도 과정에서는 A가 degenerative한 경우는 다루지 않았습니다.

3) singular $A$
만약 $A$가 rank(A) = D − 1을 만족 한다면 하나의 singular value만 0입니다. 그렇다면 아래를 두 식을 만족합니다.

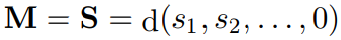
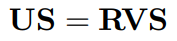
이때, orthogonal matrix K를 아래와 같이 정의 합니다.

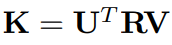
K는 아래식을 만족합니다.

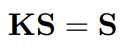
K의 column vector가 orthonormal인 것과 위의 식을 참고하면 K의 column vector에 대해서 아래의 식을 얻을 수 있습니다.

R의 constraint를 생각하면 아래의 식을 얻을 수 있습니다.

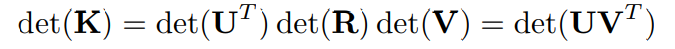
따라서, 아래의 결론을 맺을 수 있습니다.

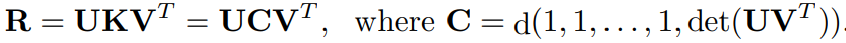
rank(A) < D − 1 일 경우에는 A가 여러개의 0인 singular values를 가지고 있습니다. 이때, K는 uniquely determined 되지 않습니다.

마치며,

closed-form solution of the rotation matrix 문제를 다루며 선형대수학의 기본적인 개념과 성질들이 우아하게 활용된다는 점을 다시 한번 느낄 수 있었습니다. 특히, 수업 시간에 쉽게 지나쳤던 trace를 기교적으로 활용하는 모습이 인상 깊네요. 조금씩 적응되는 것 같습니다! 어서, CPD를 향해 갈 수 있길!