급수의 수렴에 대해서 조사하기 위해 $S_n$의 식을 바로 알아낼 수 있다면 매우 좋겠지만,
그렇지 못한 경우가 많다.

그러나 우리의 수학자 선생님들은...
정확한 수열의 합을 알아내지 않고도 수렴과 발산을 조사할 수 있게 해놨다!!
왜 그러셨어요 ㅠㅠㅠㅠ

Integral Test

그 첫번째가 바로 Integral Test이다.

$a_n$에 상응하는 $f$에 대해서

If $\int_{1}^{\infty} f(x) dx$이 convergent(divergent)하면, $\sum_{1}^{\infty}a_n$이 convergent(divergent)하다.

Example 1

convergent한 예를 들자면, $y = 1/x^2$의 경우
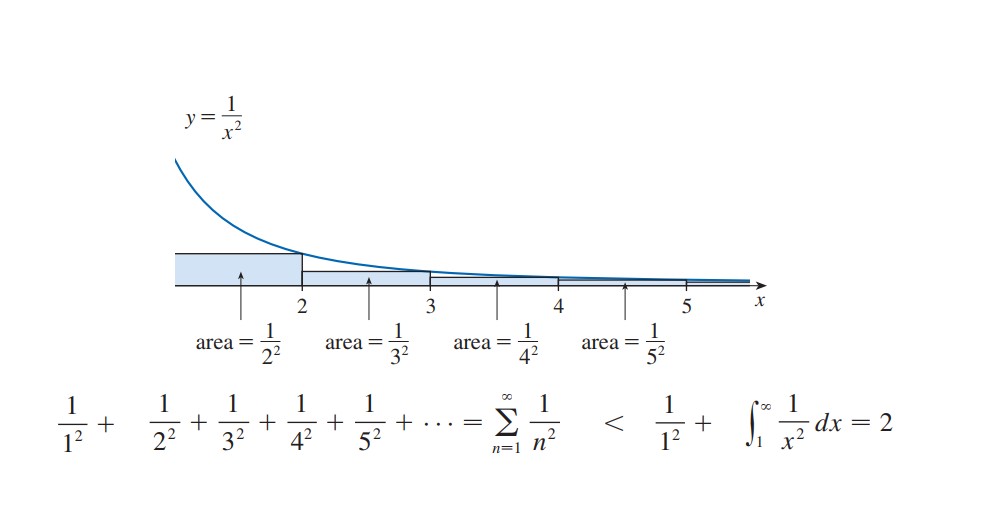출처 : calculus early transcendentals 9th edition

그림을 통해서 직사각형들(2부터 무한대)이 1부터 무한대까지의 정적분(넓이)보다 작다는 것을 알 수 있고,
양변에 1만 더해주면 그림 아래의 공식이 완성된다는 것을 알 수 있다.

Example 2

divergent한 예를 들자면, $y = 1/\sqrt{x}$의 경우

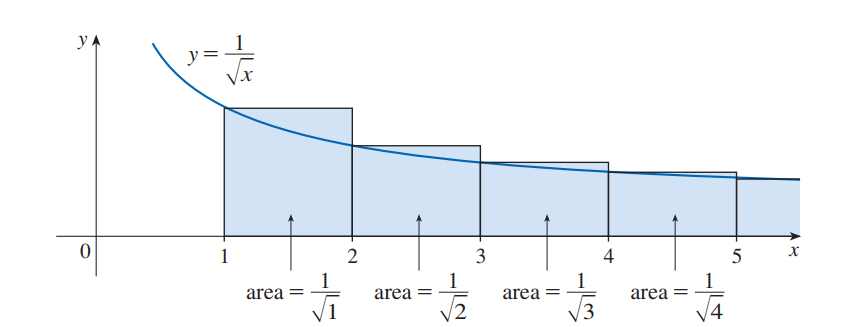
위와 달리 정적분 값보다 큰 상황. 게다가 정적분 값이 발산하기에,
당연히 네모네모들도 Divergent!

근데 애네 모양이 비슷하네...? 명칭이 따로 있을ㄹ

있다. p-series.

아하! 첫번째는 p가 2인 상황이어서 convergent, 두번째는 1/2이여서 divergent였던 것이다!

그리고 우리 잊으면 안된다! 일반적으로

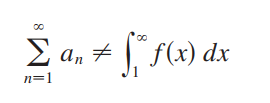
하다는 것을!

Remainder Estimate for the Integral Test

이름 왜이렇게 길어요... 어려운거 아니에요..?

아니닷! 일단 봐랏!

Remainder?

무한대까지 합친 이상적인 값 $s$와 n까지 합친 현실적인 값 $s_n$ 사이 존재하는 간극,
나머지를 Remainder, $R_n$이라고 한다.

그런데 이 친구들을 그래프로 잘 살펴보면,
왼쪽처럼 n부터 무한대까지 적분한 값보다는 작은데, n+1부터 무한대까지 적분한 값보다는 크다!

그걸 수식으로 나타내면, 다음과 같다! 이것이 바로

Remainder Estimate for the Integral Test

와!! 그러면 끝난거에요??
출처 : 나루토

Comparison Test

어림도 없다. 바로 플래그 회수

우리가 배운 모양들의 급수만 나올 것이라는 보장이 없다.
그러면 배운게 의미가 없느냐? 그건 아니올시다.

왼쪽 식처럼 우리가 배운 것과 유사한 (크거나 작은) 식이 나오면,
그 '배운 것'과 비교하여서 수렴과 발산 여부를 판단할 수 있다.

그 비교, Comparison 방법에도 두가지가 있는데,

Direct Comparison Test

말그대로 직접 비교하는 방법이다. 당연한 말이니 증명은 생략!

If $\sum b_n$이 convergent하고 $a_n \le b_n$ for all n, $\sum a_n$이 convergent하다.
If $\sum b_n$이 divergent하고 $a_n \ge b_n$ for all n, $\sum a_n$이 divergent하다.

엥 그러면

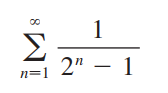
얘는 비슷한 애가 수렴하긴 하지만... 걔보단 큰걸요??

Limit Comparison Test

그럼 이걸 쓰면 된다! 증명은 간단하다.

위 가정이 성립하면, 아래 식이 성립한다.

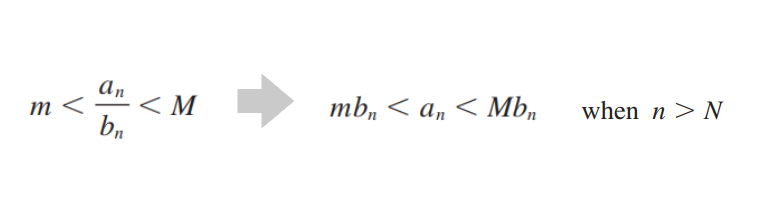
$b_n$이 coverge하는 경우, $Mb_n$ 또한 coverge하고,
그렇다면, Direct Comparison Test의 convergent 경우가 되겠다.

대략적인 설명은 끝났으니, 여러분은 왼쪽에 있는 하트를 꾸욱 눌러주시면,
고맙... 감사...황송하겠... 성은이 망극하옵니다🤞

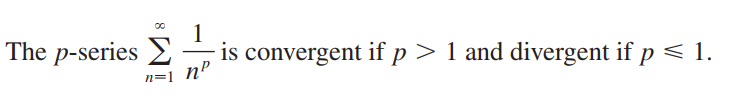
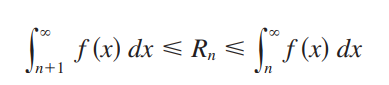
출처 : https://pbs.twimg.com/media/CQKdQPxUYAAwaqc.jpg