Batch Normalization은 2015년에 아래의 논문에서 나온 개념이다.

• Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

1. Normalization (정규화)

1.1 개념

Data Normalization은 여러 Feature 데이터 값의 범위를 사용자가 원하는 범위로 제한하는 것이다.
이미지 같은 경우 0~255 사이의 값을 가지는데, 이를 255로 나누어주면 0~1.0 사이의 값을 가지게 된다. 정규화 예시로는 Min-Max 정규화, Z-score 정규화가 있다.

1.2 정규화를 하는 이유

머신러닝 모델은 데이터가 가진 Feature을 뽑아서 학습하게 되는데 이때, 데이터의 크기가 들쑥날쑥하다면 모델이 데이터 간 편차가 큰 Feature 위주로 학습이 진행되기 때문에 모델이 데이터를 이상하게 해석할 우려가 있다.

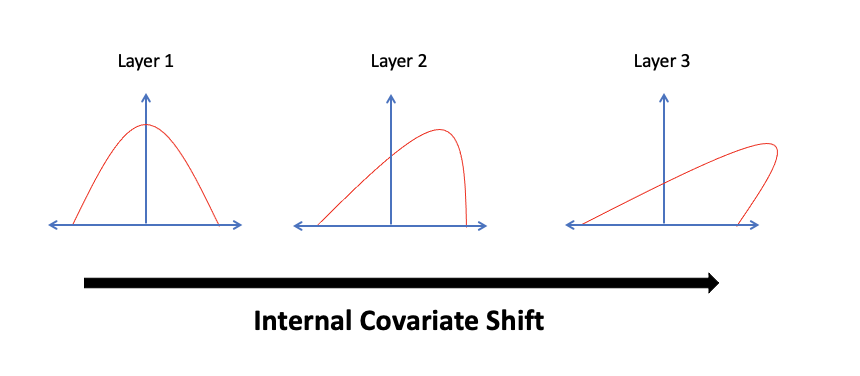
2. Internal Covariate Shift 현상

2.1 Covariate Shift

Covariate Shift는 공변량 변화라고 부르며 입력 데이터의 분포가 학습할 때와 테스트할 때 다르게 나타나는 현상을 말한다. 이는 학습 데이터를 이용해 만든 모델로 테스트 데이터셋을 추론할 때 성능에 영향을 미칠 수 있다.

2.2 Internal Covariate Shift

위 논문에서 Batch 단위로 학습하게 되면 발생하는 문제점을 Internal Covariate Shift라고 주장한다.

• Covariate Shift가 뉴럴 네트워크 내부에서 일어나는 현상을 Internal Covariate Shift라고 한다.
• Internal Covariate Shift는 네트워크의 각 Layer나 Activation마다 출력값의 데이터 분포가 Layer마다 다르게 나타나는 현상을 말한다.

2.3 문제점

Layer마다 동일한 조건으로 학습할 때, Internal Covariate Shift 현상으로 데이터 분포가 Layer마다 다르게 되어 뒷단에 위치한 Layer일 수록 변형이 누적되어 input data의 분포는 상당히 많이 달라진다. 결국, 모델의 parameter들이 일관적인 학습을 하기 어려워 학습 성능이 떨어지는 문제가 발생한다.

3. Batch Normalization (배치 정규화)

3.1 개념

• Batch Normalization은 학습 과정에서 각 배치 단위 별 다양한 분포를 가진 데이터를 각 배치별로 평균과 분산을 이용해 정규화하는 것이다.
• Batch Normalization는 별도의 과정으로 있는 것이 아닌, 신경망 안에 포함되어 학습시 평균과 분산으로 조정하는 과정이다.
• 평균은 0, 표준 편차는 1로 데이터의 분포를 조정할 수 있다.

3.2 단계별 Batch Normalization

Batch Normalization에서 중요한 것은 학습 단계와 추론 단계에서 다르게 적용되어야 한다.

3.1 학습 단계의 배치 정규화

[ 학습 단계에서의 수식 ]

$BN(X) = \gamma(\frac{X- \mu batch}{\sigma batch}) + \beta$

• $X$ : 입력 데이터
• $\gamma$ : 추가 스케일링
• $\beta$ : 편향
• $\mu batch$ : 배치 별 평균값 ($\frac{1}{B} \sum\limits_{i}x_i$)
• $\sigma batch$ : 배치별 표준 편차 ($\frac{1}{B} \sum\limits_{i}(x_i-\mu batch)^2$)

여기서 $\gamma$와 $\beta$는 training을 해야할 parameter로 사용한다. 두 값은 backporpagation을 통해 학습을 하게 된다.

• 학습 단계에서 BN을 구하기 위해서 사용된 평균과 분산을 구할 때에는 배치별로 계산된다.

• Batch Normalization은 Activation Function 앞에 적용된다.

1. Training data를 mini batch 안에서 평균과 분산을 계산

• $\mu B \leftarrow \frac{1}{m}\sum\limits_{i=1}^{m}x_i$
• $\sigma^2 B \leftarrow \frac{1}{m}\sum\limits_{i=1}^{m}(x_i-\mu B)^2$

2. 입력 데이터에 대하여 각 Feature별로 Normalization 수행

• $\hat{x}_i \leftarrow \frac{x_i - \mu B}{\sqrt{\sigma^2_B + \epsilon}}$
• $\epsilon$이 붙는 이유 : $\sigma^2 _B$가 0이 돼서 0으로 나눠지는 것을 막기 위해

3. Normalization을 한 값들에 대해 학습이 가능한 파라미터인 Scale factor(gamma)와 Shift factor(beta)를 추가

• $y_i \leftarrow \gamma\hat{x}_i + \beta \equiv BN_{\gamma,\beta}(x_i)$

만약 3번 과정 없이 ($\gamma, \beta$을 더하는 과정X) 평균이 0이고 분산이 1인 분포를 가지고 모아주기만 했다고 가정해보자.

• Activation Function가 Sigmoid 함수가 있을 때, 입력 값이 N(0,1)이 되므로 입력값의 95%은 Sigmoid 함수 그래프의 중간 구간에 속하게 된다. Sigmoid의 중간 구간은 선형이 되는 구간이기 때문에, 비선형성 성질을 잃게 되면서 Nerual Network의 성립 자체가 불가능해진다.
  
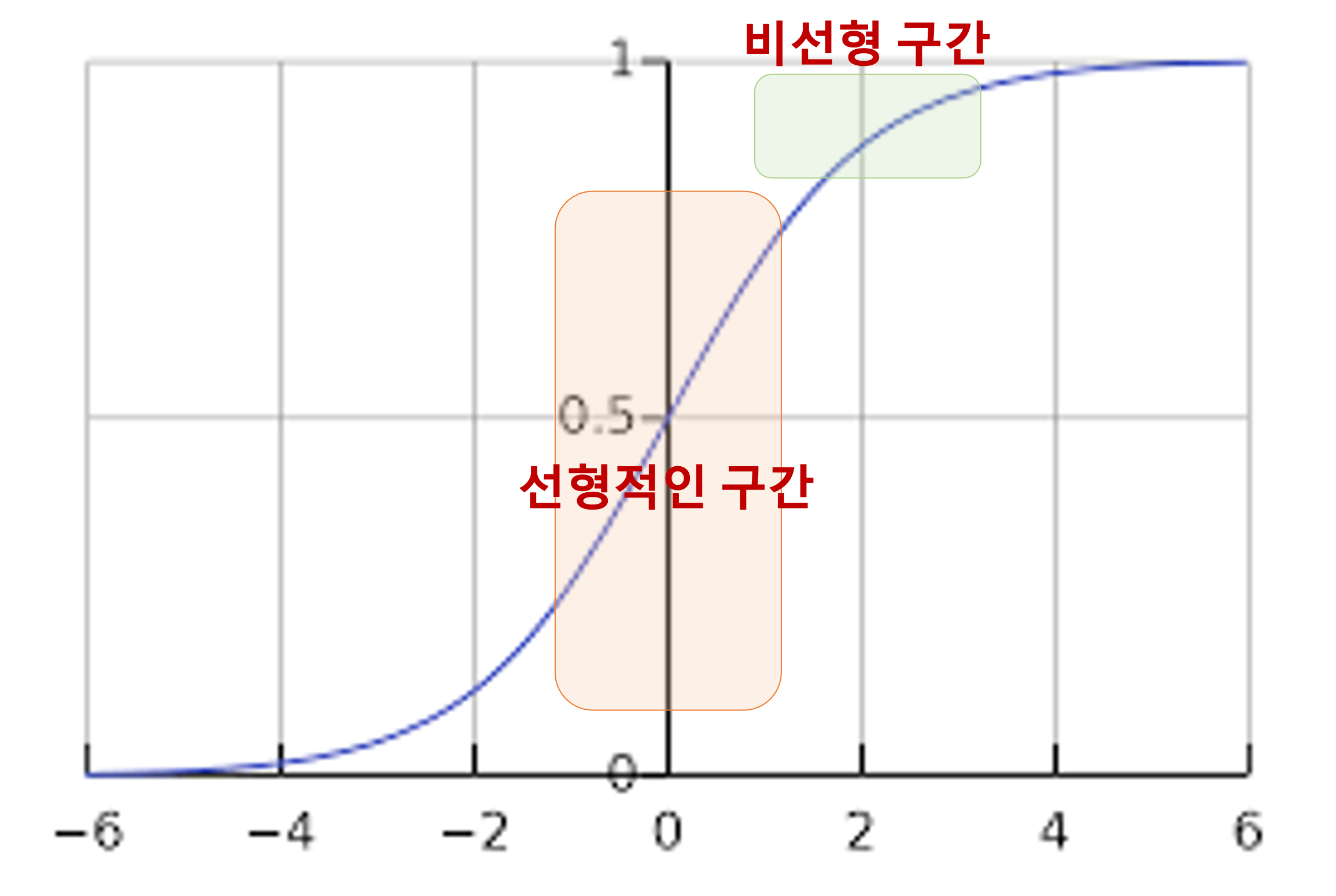
• 이 문제는 정규화 이후 사용되는 두 factor인 Scale(gamma) 및 Shift(beta) 가 학습됨에 따라 non-linearity를 유지하도록 해준다.

3.2 추론 단계의 배치 정규화

[ 추론 단계에서의 수식 ]

$BN(X) = \gamma(\frac{x-\mu BN}{\sigma BN}) + \beta$

• $\mu BN = \frac{1}{N} \sum\limits_{i} \mu ^i batch$

• $\sigma BN =\frac{1}{N}\sum\limits_{i} \sigma ^i batch$

• 추론 단계에서는 테스트 데이터에 대해 답을 내야 하므로 평균과 분산을 계산할 수 없다.

• 따라서, 추론 단계에 BN을 적용할 때는 학습 단계에서 배치 단위의 평균과 분산을 저장한 값을 이용해 정규화를 수행한다.

추론 단계에서는 학습 단계에서 모집단 추정 방식을 사용하거나 이동 평균(Moving average)과 지수 평균(exponential average)을 이용해 얻은 값을 고정된 값(평균과 분산)을 사용한다.

모집단 추정 방식

$E \left [ x^{\left(k\right)}\right] = E_{B}\left[\mu^{\left(k\right)}_{B}\right]$

$Var\left[x^{\left(k\right)}\right] = \frac{m}{m-1}E_{B}\left[\sigma^{\left(k\right)^{2}}_{B}\right]$

이동 평균(Moving average)

$\hat{\mu} \leftarrow \alpha \hat{\mu} + (1 - \alpha)\mu_\beta^{(i)}$

$\hat{\sigma} \leftarrow \alpha\hat{\sigma} + (1-\alpha)\sigma_\beta^{(i)}$

모집단 추정 방식의 경우 모든 mini batch의 평균과 분산 값들을 저장하고 있어야 하기 때문에 비효율적이다.
이 이유로 주로 이전 정보들을 바탕으로 모집단의 정보를 예측하는 방식인 Moving average방식으로 구현된다.
-> 학습 하였을 때의 최근 N 개에 대한 평균 값을 고정값으로 사용하는 것

3.4 왜 Learning rate를 키워도 될까?

평균 0, 표준 편차 1인 가운데로 값들을 뿌려주기 때문에, 입력 값들에 대한 update 해야하는 편차들이 크지 않는다. 즉, Learning rate를 크게 해도 상관없다.

결론

• 배치 정규화는 평균과 분산을 구하는 것이 아닌 $\gamma$(Scale), $\beta$(Shift)을 학습 파라미터로 사용하여 비선형성을 유지하며 학습한다.
• 배치 정규화는 별도의 과정으로 있는 것이 아닌, 신경망 안에 포함되어 학습시 평균과 분산으로 조정하는 과정이다.
• 기존 방법에서는 Learning rate를 높게 잡을 경우 gradient vanishing/explode 하는 경향이 있었었다.
• gradient의 scale, 초기값에 대한 dependency 감소 -> 배치 정규화를 사용할 경우 파라미터의 scale에 영향을 받지 않게 되기 때문에 Learning rate를 높게 설정할 수 있다. -> 빠르고 안정적인 학습이 가능해짐.
• Regularization 효과가 있기 때문에 dropout을 안해도 되는 장점이 있다.

Reference

• 배치 정규화(Batch Normalization)
• [Deep Learning] Batch Normalization(배치 정규화) 개념
• [개념 정리] Batch Normalization in Deep Learning - part 1.